Диаграмма Вороного

20 точек и их ячейки Вороного (увеличенная версия ниже )

В математике диаграмма Вороного — это разбиение плоскости на области , близкие к каждому из заданного набора объектов. Его также можно классифицировать как тесселяцию . В простейшем случае эти объекты представляют собой конечное число точек на плоскости (называемых семенами, узлами или генераторами). Для каждого семени существует соответствующая область , называемая ячейкой Вороного , состоящая из всех точек плоскости, находящихся ближе к этому семени, чем к любому другому. Диаграмма Вороного набора точек двойственна этого набора триангуляции Делоне .

Диаграмма Вороного названа в честь математика Георгия Вороного , а также называется мозаикой Вороного , разложением Вороного , разбиением Вороного или мозаикой Дирихле (в честь Питера Густава Лежена Дирихле ). Ячейки Вороного также известны как многоугольники Тиссена , в честь Альфреда Х. Тиссена . Диаграммы Вороного имеют практическое и теоретическое применение во многих областях, в основном в науке и технике , а также в изобразительном искусстве .

Самый простой случай

В простейшем случае, показанном на первой картинке, нам дан конечный набор точек $\{p_{1},\dots p_{n}\}$ в евклидовой плоскости . В этом случае каждый сайт $p_{k}$ - одна из этих заданных точек, а соответствующая ей ячейка Вороного $R_{k}$ состоит из каждой точки евклидовой плоскости, для которой $p_{k}$ ближайший объект: расстояние до $p_{k}$ меньше или равно минимальному расстоянию до любого другого объекта $p_{j}$. Для еще одного сайта $p_{j}$, точки, которые ближе к $p_{k}$ чем $p_{j}$, или одинаково удаленные, образуют замкнутое полупространство , граница которого является серединным перпендикуляром отрезка прямой $p_{j}p_{k}$. Клетка $R_{k}$ это пересечение всего этого $n-1$ полупространства, и, следовательно, это выпуклый многоугольник . Когда две ячейки на диаграмме Вороного имеют общую границу, это отрезок , луч или линия, состоящая из всех точек плоскости, которые равноудалены от двух ближайших к ним точек. Вершины . диаграммы, где встречаются три или более из этих границ, являются точками, имеющими три или более одинаково удаленных ближайших узла

Формальное определение

Позволять ${\textstyle X}$ быть метрическим пространством с функцией расстояния ${\textstyle d}$. Позволять ${\textstyle K}$ — набор индексов и пусть ${\textstyle (P_{k})_{k\in K}}$ быть кортежем (индексированной коллекцией) непустых подмножеств (сайтов) в пространстве ${\textstyle X}$. Ячейка Вороного, или область Вороного, ${\textstyle R_{k}}$, связанный с сайтом ${\textstyle P_{k}}$ это совокупность всех точек ${\textstyle X}$ расстояние до которого ${\textstyle P_{k}}$ не больше, чем их расстояние до других сайтов ${\textstyle P_{j}}$, где ${\textstyle j}$ отличается ли какой-либо индекс от ${\textstyle k}$. Другими словами, если ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ обозначает расстояние между точкой ${\textstyle x}$ и подмножество ${\textstyle A}$, затем

$$R_{k}=\{x\in X\mid d(x,P_{k})\leq d(x,P_{j})\;{\text{for all}}\;j\neq k\}$$

Диаграмма Вороного — это просто набор ячеек. ${\textstyle (R_{k})_{k\in K}}$. В принципе, некоторые сайты могут пересекаться и даже совпадать (ниже описано применение сайтов, представляющих магазины), но обычно они считаются непересекающимися. Кроме того, в определении допускается бесконечное количество узлов (эта настройка имеет приложения в геометрии чисел и кристаллографии ), но опять же во многих случаях рассматривается только конечное число узлов.

В частном случае, когда пространство представляет собой конечномерное евклидово пространство , каждый узел представляет собой точку, имеется конечное число точек и все они различны, тогда ячейки Вороного являются выпуклыми многогранниками , и их можно представить комбинаторно, используя их вершины, стороны, двумерные грани и т. д. Иногда индуцированную комбинаторную структуру называют диаграммой Вороного. Однако в целом ячейки Вороного могут быть невыпуклыми и даже не связными.

В обычном евклидовом пространстве мы можем переписать формальное определение в обычных терминах. Каждый полигон Вороного ${\textstyle R_{k}}$ связан с генераторной точкой ${\textstyle P_{k}}$.Позволять ${\textstyle X}$ — множество всех точек евклидова пространства. Позволять ${\textstyle P_{1}}$ быть точкой, которая генерирует область Вороного ${\textstyle R_{1}}$, ${\textstyle P_{2}}$ который генерирует ${\textstyle R_{2}}$, и ${\textstyle P_{3}}$ который генерирует ${\textstyle R_{3}}$, и так далее. Тогда, как выразились Тран и др ., «все местоположения в многоугольнике Вороного находятся ближе к образующей точке этого многоугольника, чем любая другая образующая точка на диаграмме Вороного в евклидовой плоскости».

Иллюстрация

В качестве простой иллюстрации рассмотрим группу магазинов в городе. Предположим, мы хотим оценить количество покупателей данного магазина. При прочих равных условиях (цена, продукция, качество обслуживания и т. д.) разумно предположить, что покупатели выбирают предпочитаемый магазин просто по соображениям расстояния: они пойдут в ближайший к ним магазин. В этом случае ячейка Вороного $R_{k}$ данного магазина $P_{k}$ можно использовать для приблизительной оценки количества потенциальных покупателей, посещающих этот магазин (который моделируется точкой в ​​нашем городе).

Для большинства городов расстояние между точками можно измерить с помощью привычного нам метода. Евклидово расстояние :

$\ell _{2}=d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]={\sqrt {\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}}}$

или Манхэттенское расстояние :

$d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|$.

Соответствующие диаграммы Вороного выглядят по-разному для разных метрик расстояния.

Диаграммы Вороного по 20 точкам по двум разным метрикам

Евклидово расстояние

Расстояние Манхэттен

Свойства

• Двойственный граф диаграммы Вороного (в случае евклидова пространства с точечными узлами) соответствует триангуляции Делоне для того же набора точек.
• Ближайшая пара точек соответствует двум соседним ячейкам диаграммы Вороного.
• Предположим, что задана евклидова плоскость и задан дискретный набор точек. Тогда две точки множества смежны на выпуклой оболочке тогда и только тогда, когда их ячейки Вороного имеют бесконечно длинную сторону.
• Если пространство является нормированным пространством и расстояние до каждого узла достигнуто (например, когда узел представляет собой компакт или замкнутый шар), то каждую ячейку Вороного можно представить как объединение отрезков, исходящих из узлов. Как показано там, это свойство не обязательно сохраняется, если расстояние не достигнуто.
• При относительно общих условиях (пространство является, возможно, бесконечномерным равномерно выпуклым пространством , узлов общего вида может быть бесконечно много и т. д.) ячейки Вороного обладают определенным свойством устойчивости: небольшим изменением формы узлов, напр. , изменение, вызванное некоторой трансляцией или искажением, приводит к небольшому изменению формы ячеек Вороного. В этом заключается геометрическая устойчивость диаграмм Вороного. Как показано там, это свойство, вообще говоря, не выполняется, даже если пространство двумерно (но неравномерно выпукло и, в частности, неевклидово) и узлы являются точками.

и

Неофициальное использование диаграмм Вороного восходит к Декарту в 1644 году. Питер Густав Лежен Дирихле использовал двумерные и трехмерные диаграммы Вороного в своем исследовании квадратичных форм в 1850 году.Британский врач Джон Сноу использовал диаграмму, подобную Вороному, в 1854 году, чтобы проиллюстрировать, как большинство людей, умерших во время вспышки холеры на Брод-стрит, жили ближе к зараженному насосу на Брод-стрит, чем к любому другому водяному насосу.

Диаграммы Вороного названы в честь Георгия Феодосьевича Вороного, который определил и изучил общий n -мерный случай в 1908 году. Диаграммы Вороного, которые используются в геофизике и метеорологии для анализа пространственно распределенных данных, называются полигонами Тиссена в честь американского метеоролога Альфреда Х. Тиссена , который использовал их для оценки количества осадков на основе разрозненных измерений в 1911 году. Другие эквивалентные названия для этой концепции (или отдельных важных случаев it): многогранники Вороного, многоугольники Вороного, область(и) влияния, разложение Вороного, мозаика(ы) Вороного, мозаика(ы) Дирихле.

Примеры

Это фрагмент диаграммы Вороного случайного набора точек в трехмерном блоке. В общем, поперечное сечение трехмерной мозаики Вороного представляет собой степенную диаграмму , взвешенную форму двумерной диаграммы Вороного, а не невзвешенную диаграмму Вороного.

Мозаики Вороного из регулярных решеток точек в двух или трех измерениях порождают многие знакомые мозаики.

• 2D-решетка представляет собой неправильную сотовую мозаику с одинаковыми шестиугольниками с точечной симметрией; в случае правильной треугольной решетки она правильна; в случае прямоугольной решетки шестиугольники сводятся к прямоугольникам в строках и столбцах; квадратная ; решетка дает правильную мозаику квадратов обратите внимание, что прямоугольники и квадраты также могут быть созданы другими решетками (например, решетка, определяемая векторами (1,0) и (1/2,1/2), дает квадраты).
• Простая кубическая решетка дает кубические соты .
• Шестиугольная плотноупакованная решетка дает замощение пространства трапезо-ромбическими додекаэдрами .
• Гробоцентрированная кубическая решетка дает замощение пространства ромбическими додекаэдрами .
• Объемноцентрированная кубическая решетка дает мозаику пространства усеченными октаэдрами .
• Параллельные плоскости с правильными треугольными решетками, совмещенными с центрами друг друга, образуют шестиугольные призматические соты .
• Определенные объемноцентрированные тетрагональные решетки образуют мозаику пространства с ромбо-шестиугольными додекаэдрами .

Определенные объемноцентрированные тетрагональные решетки образуют мозаику пространства с ромбо-шестиугольными додекаэдрами .

Для набора точек ( x , y ) с x в дискретном множестве X и y в дискретном множестве Y мы получаем прямоугольные плитки с точками не обязательно в их центрах.

высшего

Хотя нормальная ячейка Вороного определяется как набор точек, ближайших к одной точке в S , ячейка Вороного n -го порядка определяется как набор точек, имеющих конкретный набор из n точек в S в качестве n ближайших соседей. Диаграммы Вороного высшего порядка также подразделяют пространство.

Диаграммы Вороного высшего порядка можно генерировать рекурсивно. Чтобы сгенерировать n ^й Диаграмма Вороного -порядка из множества S , начните с ( n − 1) ^й -порядка и замените каждую ячейку, порожденную X = { x ₁ , x ₂ , ..., x _{n −1} }, диаграммой Вороного, порожденной на множестве S − X .

дальней

Для набора из n точек ( n − 1) ^й Диаграмма Вороного -порядка называется диаграммой Вороного в самой дальней точке.

Для данного набора точек S = { p ₁ , p ₂ , ..., p _n } диаграмма Вороного самой дальней точки делит плоскость на ячейки, в которых одна и та же точка P является самой дальней точкой. Точка P точки тогда и только тогда, когда она является вершиной выпуклой оболочки P имеет ячейку в диаграмме Вороного самой дальней . Пусть H = { h ₁ , h ₂ , ..., h _k } — выпуклая оболочка P ; тогда диаграмма Вороного с самой дальней точкой представляет собой подразделение плоскости на k ячеек, по одной для каждой точки в H , со свойством, что точка q лежит в ячейке, соответствующей узлу h _i тогда и только тогда, когда d( q , h _i ) > d( q , p _j ) для каждого p _j ∈ S с h _i ≠ p _j , где d( p , q ) — евклидово расстояние между двумя точками p и q .

Границы ячеек диаграммы Вороного в самой дальней точке имеют структуру топологического дерева с бесконечными лучами в качестве его листьев. Каждое конечное дерево изоморфно дереву, сформированному таким образом из диаграммы Вороного в самой дальней точке.

Обобщения и вариации

Как следует из определения, ячейки Вороного могут быть определены для метрик, отличных от евклидовых, таких как расстояние Махаланобиса или расстояние Манхэттена . Однако в этих случаях границы ячеек Вороного могут быть более сложными, чем в евклидовом случае, поскольку эквидистантное множество для двух точек может не быть подпространством коразмерности 1 даже в двумерном случае.

Приближенная диаграмма Вороного множества точек. Обратите внимание на смешанные цвета на нечеткой границе ячеек Вороного.

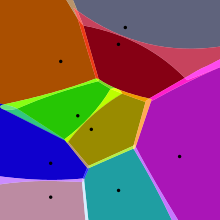
Взвешенная диаграмма Вороного — это диаграмма, в которой функция пары точек, определяющая ячейку Вороного, представляет собой функцию расстояния, модифицированную мультипликативными или аддитивными весами, присвоенными точкам генератора. В отличие от случая ячеек Вороного, определяемых с использованием расстояния, которое является метрикой , в этом случае некоторые ячейки Вороного могут быть пустыми. Диаграмма мощности — это тип диаграммы Вороного, определяемой из набора кругов с использованием расстояния власти ; ее также можно рассматривать как взвешенную диаграмму Вороного, в которой вес, определенный исходя из радиуса каждого круга, добавляется к квадрату евклидова расстояния от центра круга.

Диаграмма Вороного $n$ указывает на $d$-мерное пространство может иметь ${\textstyle O(n^{\lceil d/2\rceil })}$ вершин, требуя одинаковой оценки объема памяти, необходимой для хранения ее явного описания. Поэтому диаграммы Вороного часто неприменимы для средних или больших размерностей. Более экономичная альтернатива — использовать приближенные диаграммы Вороного .

Диаграммы Вороного также связаны с другими геометрическими структурами, такими как медиальная ось (которая нашла применение в сегментации изображений, оптическом распознавании символов и других вычислительных приложениях), прямой скелет и диаграммы зон .

Приложения

Метеорология/Гидрология

Он используется в метеорологии и инженерной гидрологии для определения весов данных об осадках на станциях по территории (водоразделу). Точками, образующими полигоны, являются различные станции, записывающие данные об осадках. К линии, соединяющей любые две станции, проводят биссектрисы. Это приводит к образованию полигонов вокруг станций. Район $(A_{i})$ точка касания станции известна как зона влияния станции. Среднее количество осадков рассчитывается по формуле ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$

См. Также: Триангуляция Делоне § Приложения.

и

• В классической археологии , особенно в истории искусства , симметрия голов статуй анализируется, чтобы определить тип статуи, которой могла принадлежать отрубленная голова. Примером использования ячеек Вороного была идентификация головы Сабурова , в которой использовалась полигональная сетка высокого разрешения .
• В диалектометрии ячейки Вороного используются для обозначения предполагаемой лингвистической преемственности между точками исследования.
• В политологии диаграммы Вороного использовались для изучения многомерной, многопартийной конкуренции.

Естественные науки

Мозаика Вороного возникает в результате радиального роста семян наружу.

• В биологии диаграммы Вороного используются для моделирования ряда различных биологических структур, включая клетки. и микроархитектура кости. Действительно, мозаика Вороного работает как геометрический инструмент, позволяющий понять физические ограничения, которые управляют организацией биологических тканей.
• В гидрологии диаграммы Вороного используются для расчета количества осадков на определенной территории на основе серии точечных измерений. В таком случае их обычно называют полигонами Тиссена.
• В экологии диаграммы Вороного используются для изучения закономерностей роста лесов и лесных пологов, а также могут быть полезны при разработке моделей прогнозирования лесных пожаров.
• В этологии диаграммы Вороного используются для моделирования областей опасности в теории эгоистичного стада .
• В вычислительной химии сайты связывания лигандов преобразуются в диаграммы Вороного для приложений машинного обучения (например, для классификации карманов связывания в белках). используются ячейки Вороного, определяемые положениями ядер в молекуле В других приложениях для вычисления атомных зарядов . Это делается с помощью метода плотности деформации Вороного .
• В астрофизике диаграммы Вороного используются для формирования зон адаптивного сглаживания на изображениях, складывая потоки сигналов на каждой из них. Основная цель этих процедур — поддерживать относительно постоянное соотношение сигнал/шум на всех изображениях.
• В вычислительной гидродинамике мозаика Вороного набора точек может использоваться для определения вычислительных областей, используемых в методах конечных объемов , например, как в космологическом коде с подвижной сеткой AREPO.
• В вычислительной физике диаграммы Вороного используются для расчета профилей объекта с помощью Shadowgraph и протонной радиографии в физике высокой плотности энергии .

Здоровье

• В медицинской диагностике модели мышечной ткани, основанные на диаграммах Вороного, могут использоваться для выявления нервно-мышечных заболеваний.
• В эпидемиологии диаграммы Вороного можно использовать для корреляции источников инфекций при эпидемиях. Одно из первых применений диаграмм Вороного было применено Джоном Сноу для изучения вспышки холеры на Брод-стрит в 1854 году в Сохо, Англия. Он показал корреляцию между жилыми районами на карте центрального Лондона, жители которых пользовались определенным водяным насосом, и районами с наибольшим количеством смертей из-за вспышки.

Инженерное дело

• В физике полимеров диаграммы Вороного можно использовать для представления свободных объемов полимеров.
• В материаловедении поликристаллические микроструктуры в металлических сплавах обычно представляют с помощью мозаик Вороного.
• При росте островов диаграмма Вороного используется для оценки скорости роста отдельных островов.
• В физике твердого тела ячейка Вигнера -Зейтца представляет собой мозаику Вороного твердого тела, а зона Бриллюэна — мозаику Вороного обратного ( волнового числа ) пространства кристаллов, обладающих симметрией пространственной группы.
• В авиации диаграммы Вороного накладываются на океанические карты, чтобы определить ближайший аэродром для отклонения в полете (см. ETOPS ) по мере выполнения самолета по плану полета.
• В архитектуре образцы Вороного легли в основу победившей работы по реконструкции Центра искусств Голд-Кост .
• В городском планировании диаграммы Вороного можно использовать для оценки системы зон погрузки грузов.
• В горнодобывающей промышленности полигоны Вороного используются для оценки запасов ценных материалов, полезных ископаемых или других ресурсов. В качестве набора точек на полигонах Вороного используются разведочные скважины.
• В метрологии поверхности тесселяция Вороного может использоваться для шероховатости поверхности . моделирования
• В робототехнике некоторые стратегии управления и алгоритмы планирования пути многороботных систем основаны на разбиении среды Вороного.

Математика

• Структура данных о местоположении точки может быть построена поверх диаграммы Вороного, чтобы отвечать на запросы ближайших соседей , когда нужно найти объект, ближайший к данной точке запроса. Запросы ближайших соседей имеют множество применений. Например, можно захотеть найти ближайшую больницу или наиболее похожий объект в базе данных . Большим применением является векторное квантование , обычно используемое при сжатии данных .
• В геометрии диаграммы Вороного можно использовать для поиска наибольшего пустого круга среди набора точек и во вмещающем многоугольнике; например, построить новый супермаркет как можно дальше от всех существующих, находящихся в определенном городе.
• Диаграммы Вороного вместе с диаграммами Вороного для самой дальней точки используются для эффективных алгоритмов вычисления округлости набора точек. Подход Вороного также применяется при оценке округлости/ круглости при оценке набора данных с координатно-измерительной машины .
• Нули повторных производных рациональной функции на комплексной плоскости накапливаются на краях диаграммы Вороного множества полюсов ( теорема Пойа о графстве ).

Информатика

• В сетях диаграммы Вороного могут быть использованы для определения пропускной способности беспроводной сети .
• В компьютерной графике диаграммы Вороного используются для расчета трехмерных геометрических моделей разрушения/разрыва. Он также используется для процедурного создания органических текстур или текстур, похожих на лаву.
• В автономной навигации роботов диаграммы Вороного используются для поиска четких маршрутов. Если точки являются препятствиями, то ребрами графа будут маршруты, наиболее удаленные от препятствий (и теоретически от любых столкновений).
• В машинном обучении диаграммы Вороного используются для классификации 1-NN .
• При глобальной реконструкции сцены, в том числе со случайными местоположениями датчиков и нестационарным следом, геофизическими данными и трехмерными данными турбулентности, тесселяции Вороного используются с глубоким обучением .
• При разработке пользовательского интерфейса шаблоны Вороного можно использовать для вычисления наилучшего состояния наведения для заданной точки.

и

• В Мельбурне учащиеся государственных школ всегда имеют право посещать ближайшую к месту их проживания начальную или среднюю школу, если измерять расстояние по прямой. Таким образом, карта школьных зон представляет собой диаграмму Вороного.

Пекарня

• Украинский кондитер Динара Касько использует математические принципы диаграммы Вороного для создания силиконовых форм, изготовленных на 3D-принтере, для придания формы своим оригинальным тортам.

Алгоритмы

Известно несколько эффективных алгоритмов построения диаграмм Вороного либо напрямую (как сама диаграмма), либо косвенно, начиная с триангуляции Делоне и затем получая ее двойственную.К прямым алгоритмам относится алгоритм Форчуна — алгоритм O ( n log( n )) для генерации диаграммы Вороного из набора точек на плоскости. Алгоритм Бойера–Ватсона , от O ( n log( n )) до O ( n ² ) алгоритм построения триангуляции Делоне в любом количестве измерений, может быть использован в косвенном алгоритме для диаграммы Вороного. Алгоритм Jump Flooding может генерировать приблизительные диаграммы Вороного за постоянное время и подходит для использования на обычном графическом оборудовании.

Алгоритм Ллойда и его обобщение с помощью алгоритма Линде – Бьюзо – Грея (также известного как кластеризация k-средних ) используют построение диаграмм Вороного в качестве подпрограммы.Эти методы чередуются между этапами построения диаграммы Вороного для набора исходных точек и этапами, на которых исходные точки перемещаются в новые места, которые являются более центральными внутри своих ячеек. Эти методы можно использовать в пространствах произвольной размерности для итеративной сходимости к специализированной форме диаграммы Вороного, называемой центроидальной мозаикой Вороного , где узлы перемещаются в точки, которые также являются геометрическими центрами их ячеек.

Voronoi in 3D

Сетки Вороного также можно создавать в 3D.

• 
  Случайные точки в 3D для формирования 3D-раздела Вороного
• 
  3D Voronoi mesh of 25 random points
• 
  3D-сетка Вороного из 25 случайных точек с непрозрачностью 0,3 и точками
• 
  3D-сетка Вороного из 25 случайных точек частей выпуклых многогранников

См. также

• Триангуляция Делоне
• Сегментация карты
• Метод природных элементов
• Интерполяция естественных соседей
• Интерполяция ближайшего соседа
• Схема мощности
• Вороной полюс

Ссылки

• Ауренхаммер, Франц ; Кляйн, Рольф; Ли, Дер-Цай (2013). Диаграммы Вороного и триангуляции Делоне . Всемирная научная. ISBN  978-9814447638 .
• Бойер, Адриан (1981). «Вычисление мозаики Дирихле» . Вычислить. Дж. 24 (2): 162–166. дои : 10.1093/comjnl/24.2.162 .
• де Берг, Марк; ван Кревелд, Марк; Овермарс, Марк ; Шварцкопф, Отфрид (2000). «7. Диаграммы Вороного» . Вычислительная геометрия (2-е исправленное изд.). Спрингер. стр. 47–163. ISBN  978-3-540-65620-3 . Включает описание алгоритма Фортуны.
• Кляйн, Рольф (1988). «Абстрактные диаграммы Вороного и их приложения: Расширенный реферат». Вычислительная геометрия и ее приложения . Конспекты лекций по информатике . Том. 333. Спрингер. стр. 148–157. дои : 10.1007/3-540-50335-8_31 . ISBN  978-3-540-52055-9 .
• Лежен Дирихле, Ж. (1850). «О приведении положительных квадратичных форм с тремя неопределенными целыми числами». Журнал чистой и прикладной математики . 1850 (40): 209–227. дои : 10.1515/crll.1850.40.209 . S2CID   199546675 .
• Окабе, Ацуюки; Бутс, Барри; Сугихара, Кокичи ; Чиу, Сунг Нок (2000). Пространственные замощения - концепции и применение диаграмм Вороного (2-е изд.). Уайли. ISBN  0-471-98635-6 .
• Рим, Дэниел (2009). «Алгоритм вычисления диаграмм Вороного общих генераторов в общих нормированных пространствах». Материалы шестого международного симпозиума по диаграммам Вороного в науке и технике (ISVD 2009) . стр. 144–152. дои : 10.1109/ИСВД.2009.23 . ISBN  978-1-4244-4769-5 .
• Рим, Дэниел (2011). «Геометрическая устойчивость диаграмм Вороного относительно небольших изменений узлов». Материалы двадцать седьмого ежегодного симпозиума по вычислительной геометрии . стр. 254–263. arXiv : 1103.4125 . Бибкод : 2011arXiv1103.4125R . дои : 10.1145/1998196.1998234 . ISBN  9781450306829 . S2CID   14639512 .
• Тиссен, Альфред Х. (июль 1911 г.). «Среднее количество осадков на больших территориях» . Ежемесячный обзор погоды . 39 (7). Американское метеорологическое общество: 1082–1089. Бибкод : 1911MWRv...39R1082T . doi : 10.1175/1520-0493(1911)39<1082b:pafla>2.0.co;2 .
• Вороной, Жорж (1908а). «Новые приложения непрерывных параметров к теории квадратичных форм. Первая диссертация. О некоторых свойствах совершенных положительных квадратичных форм» (PDF) . Журнал для королевы и математики . 1908 (133): 97–178. дои : 10.1515/crll.1908.133.97 . S2CID   116775758 .
• Вороной, Жорж (1908b). «Новые применения непрерывных параметров в теории квадратичных форм. Вторая диссертация. Исследование примитивных параллелоэдров» (PDF) . Журнал для королевы и математики . 1908 (134): 198–287. дои : 10.1515/crll.1908.134.198 . S2CID   118441072 .
• Уотсон, Дэвид Ф. (1981). «Вычисление n- мерной мозаики Делоне с применением к многогранникам Вороного» . Вычислить. Дж. 24 (2): 167–172. дои : 10.1093/comjnl/24.2.167 .

Внешние ссылки

• Вайсштейн, Эрик В. «Диаграмма Вороного» . Математический мир .
• Диаграммы Вороного в CGAL , библиотеке алгоритмов вычислительной геометрии
• Демонстрационная программа для алгоритма SFTessellation, которая создает диаграмму Вороного с использованием модели степного пожара.