Схема мощности

В вычислительной геометрии , степенная диаграмма также называемая диаграммой Лагерра-Вороного , комплексом ячеек Дирихле , радикальной мозаикой Вороного или секционной мозаикой Дирихле , представляет собой разделение евклидовой плоскости на многоугольные ячейки, определенные из набора кругов. Ячейка для данного круга C состоит из всех точек, для которых расстояние власти до C меньше, чем расстояние власти до других кругов. Степенная диаграмма является формой обобщенной диаграммы Вороного и совпадает с диаграммой Вороного центров окружностей в случае, когда все окружности имеют равные радиусы. [1] [2] [3] [4]
Определение
[ редактировать ]
Если C — круг, а — точка вне C , то степень P C по отношению к P это квадрат длины отрезка прямой от P до точки T касания с C. — Эквивалентно, если P находится на расстоянии d от центра круга, а круг имеет радиус r , то (по теореме Пифагора ) степень равна d 2 − р 2 . Та же формула д 2 − р 2 может быть распространено на все точки плоскости, независимо от того, находятся ли они внутри или снаружи C : точки на C имеют нулевую мощность, а точки внутри C имеют отрицательную мощность. [2] [3] [4]
Степенная диаграмма набора из n кругов C i представляет собой разбиение плоскости на n областей R i (называемых ячейками), так что точка P принадлежит R i всякий раз, когда круг C i является кругом, минимизирующим степень P . [2] [3] [4]
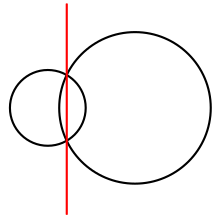
В случае n = 2 степенная диаграмма состоит из двух полуплоскостей , разделенных линией, называемой радикальной осью или хордалой двух окружностей. Вдоль радикальной оси оба круга имеют равную власть. В более общем смысле, в любой степенной диаграмме каждая ячейка R i представляет собой выпуклый многоугольник , пересечение полупространств, ограниченных радикальными осями окружности C i, друг с другом. Тройки ячеек встречаются в вершинах диаграммы, которые являются радикальными центрами трех кругов, ячейки которых встречаются в вершине. [2] [3] [4]
Связанные конструкции
[ редактировать ]Диаграмму мощности можно рассматривать как взвешенную форму диаграммы Вороного набора точечных узлов, разбиения плоскости на ячейки, внутри которых один из узлов находится ближе, чем все остальные. Другие формы взвешенной диаграммы Вороного включают аддитивно взвешенную диаграмму Вороного, в которой каждый узел имеет вес, который добавляется к его расстоянию перед сравнением его с расстояниями до других узлов, и мультипликативно взвешенную диаграмму Вороного, в которой вес сайта умножается на его расстояние перед сравнением с расстояниями до других сайтов. Напротив, на диаграмме мощности мы можем рассматривать каждый центр круга как точку, а квадрат радиуса каждого круга - как вес, который вычитается из квадрата евклидова расстояния перед сравнением его с другими квадратами расстояний. В случае, когда все радиусы окружностей равны, это вычитание не имеет значения для сравнения, и степенная диаграмма совпадает с диаграммой Вороного. [3] [4]
Плоскую диаграмму мощности также можно интерпретировать как плоское сечение невзвешенной трехмерной диаграммы Вороного. В этой интерпретации набор центров окружностей в плоскости поперечного сечения представляет собой перпендикулярные проекции трехмерных узлов Вороного, а квадрат радиуса каждого круга представляет собой константу K минус квадрат расстояния соответствующего узла от сечения. плоскость сечения, где K выбран достаточно большим, чтобы все эти радиусы были положительными. [5]
Как и диаграмма Вороного, степенная диаграмма может быть обобщена на евклидовы пространства любой размерности. Степенная диаграмма n сфер в d измерениях комбинаторно эквивалентна пересечению набора из n обращенных вверх полупространств в d + 1 измерениях, и наоборот. [3]
Алгоритмы и приложения
[ редактировать ]Двумерные диаграммы мощности могут быть построены с помощью алгоритма, работающего за время O( n log n ). [2] [3] В более общем смысле, из-за эквивалентности с пересечениями полупространств более высокой размерности, d -мерные степенные диаграммы (для d > 2) могут быть построены с помощью алгоритма, работающего во времени. . [3]
Степенную диаграмму можно использовать как часть эффективного алгоритма вычисления объема объединения сфер. Пересечение каждой сферы с ячейкой ее энергетической диаграммы дает ее вклад в общее объединение, из которого можно вычислить объем за время, пропорциональное сложности степенной диаграммы. [6]
Другие применения диаграмм мощности включают структуры данных для проверки принадлежности точки объединению дисков. [2] алгоритмы построения границы объединения дисков, [2] и алгоритмы поиска двух ближайших шаров в наборе шаров. [7] Он также используется для решения полудискретной оптимальной транспортировки . задачи [8] что, в свою очередь, имеет множество приложений, таких как реконструкция ранней Вселенной. [9] или гидродинамика. [10]
История
[ редактировать ]Ауренхаммер (1987) прослеживает определение дистанции власти до работ математиков XIX века Эдмона Лагерра и Георгия Вороного . [3] Фейес Тот (1977) определил диаграммы мощности и использовал их, чтобы показать, что граница объединения n круглых дисков всегда может быть освещена не более чем 2 n точечными источниками света. [11] Силовые диаграммы появлялись в литературе под другими названиями, включая «диаграмма Лагерра – Вороного», «комплекс клеток Дирихле», «радикальная мозаика Вороного» и «секционная мозаика Дирихле». [12]
Ссылки
[ редактировать ]- ^ ( Линхарт Дж. , ) 1981 10.1007/BF00149360, MR 0627538, S2CID 120072781.
- ^ Jump up to: Перейти обратно: а б с д и ж г Имаи, Хироши; Ири, Масао; Мурота, Кадзуо (1985), «Диаграмма Вороного в геометрии Лагерра и ее приложения», SIAM Journal on Computing , 14 (1): 93–105, doi : 10.1137/0214006 , MR 0774929 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Ауренхаммер, Ф. (1987), «Степенные диаграммы: свойства, алгоритмы и приложения», SIAM Journal on Computing , 16 (1): 78–96, doi : 10.1137/0216006 , MR 0873251 .
- ^ Jump up to: Перейти обратно: а б с д и Эдельсбруннер, Герберт (1987), «13.6 Степенные диаграммы», Алгоритмы в комбинаторной геометрии , Монографии EATCS по теоретической информатике, том. 10, Springer-Verlag, стр. 327–328 .
- ^ Эш, Питер Ф.; Болкер, Итан Д. (1986), «Обобщенные мозаики Дирихле», Applied Geometry , 20 (2): 209–243, doi : 10.1007/BF00164401 , MR 0833848 , S2CID 120383767 .
- ^ Авис, Дэвид ; Бхаттачарья, Бинай К.; Имаи, Хироши (1988), «Вычисление объема объединения сфер» (PDF) , The Visual Computer , 3 (6): 323–328, doi : 10.1007/BF01901190 .
- ^ Гибас, Леонидас ; Чжан, Ли (1998), «Евклидова близость и степенные диаграммы», 10-я Канадская конференция по вычислительной геометрии .
- ^ Ауренхаммер, Ф.; Хоффманн, Ф.; Аронов, Б. (январь 1998 г.). «Теоремы типа Минковского и кластеризация по методу наименьших квадратов» . Алгоритмика . 20 (1): 61–76. дои : 10.1007/PL00009187 . ISSN 0178-4617 . S2CID 5409198 .
- ^ Леви, Бруно; Мохаяи, Ройя; фон Хаузеггер, Себастьян (13 июля 2021 г.). «Быстрый полудискретный оптимальный транспортный алгоритм для уникальной реконструкции ранней Вселенной» . Ежемесячные уведомления Королевского астрономического общества . 506 (1): 1165–1185. arXiv : 2012.09074 . дои : 10.1093/mnras/stab1676 . ISSN 0035-8711 .
- ^ Леви, Бруно (февраль 2022 г.). «Частичный оптимальный транспорт для лагранжевой сетки постоянного объема со свободными границами» . Журнал вычислительной физики . 451 : 110838. arXiv : 2106.03936 . Бибкод : 2022JCoPh.45110838L . дои : 10.1016/j.jcp.2021.110838 . S2CID 235406800 .
- ^ Фейес Тот, Л. (1977), «Освещение выпуклых дисков», Математический журнал Венгерской академии наук , 29 (3–4): 355–360, doi : 10.1007/BF01895856 , MR 0464065 , S2CID 122510545 .
- ^ Ауренхаммер, Ф.; Имаи, Х. (1988), «Геометрические отношения между диаграммами Вороного», Geometriae Dedicata , 27 (1): 65–75, doi : 10.1007/BF00181613 , MR 0950323 .
