Треугольная плитка порядка 7

Треугольная плитка порядка 7
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая регулярная мозаика
Конфигурация вершин	3 ⁷
Символ Шлефли	{3,7}
Символ Витхоффа	7 \| 3 2
Диаграмма Кокстера
Группа симметрии	[7,3], (*732)
Двойной	Семиугольная плитка
Характеристики	Вершинно-транзитивный , ребро-транзитивный , грани-транзитивный

В геометрии треугольное замощение порядка 7 представляет собой регулярное замощение гиперболической плоскости с символом Шлефли {3,7}.

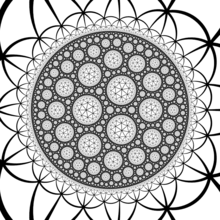
Поверхности Гурвица [ править ]

Группа симметрии мозаики — это группа треугольников (2,3,7) , а фундаментальной областью для этого действия является (2,3,7) треугольник Шварца . Это наименьший гиперболический треугольник Шварца, и, таким образом, согласно доказательству теоремы Гурвица об автоморфизмах , замощение - это универсальное замощение, которое покрывает все поверхности Гурвица ( римановы поверхности с максимальной группой симметрии), давая им триангуляцию, группа симметрии которой равна их автоморфизму. группируются как римановы поверхности.

Наименьшей из них является квартика Клейна , наиболее симметричная поверхность рода 3, вместе с мозаикой из 56 треугольников, встречающихся в 24 вершинах, с группой симметрии - простой группой порядка 168, известной как PSL(2,7) . Полученную поверхность, в свою очередь, можно многогранно погрузить в евклидово трехмерное пространство, в результате чего получится небольшой кубооктаэдр . ^[1]

Двойственная семиугольная мозаика третьего порядка имеет ту же группу симметрии и, таким образом, дает семиугольную мозаику поверхностей Гурвица.

Группа симметрии треугольной мозаики порядка 7 имеет фундаментальную область (2,3,7) треугольник Шварца , которая и дает эту мозаику.	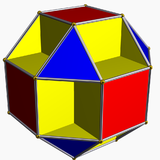Малый кубооктаэдр представляет собой многогранное погружение квартики Клейна , ^[1] которая, как и все поверхности Гурвица , является фактором этого разбиения.

Связанные многогранники и мозаика [ править ]

Он связан с двумя звездчатыми мозаиками одним и тем же расположением вершин : гептаграммной мозаикой 7-го порядка , {7/2,7} и семиугольной мозаикой гептаграммного порядка , {7,7/2}.

Это разбиение топологически связано как часть последовательности правильных многогранников с символом Шлефли {3,p}.

* n 32 мутация симметрии правильных мозаик: {3, n } v т и
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic

3.3	3³	3⁴	3⁵	3⁶	3⁷	3⁸	3^∞	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

Это замощение является частью регулярного ряда { n ,7}:

Плитки вида { n ,7}
Spherical	Hyperbolic tilings v t e
{2,7}	{3,7}	{4,7}	{5,7}	{6,7}	{7,7}	{8,7}	...	{∞,7}

Из конструкции Витгофа есть восемь гиперболических однородных мозаик , которые могут быть основаны на регулярной семиугольной мозаике.

Если нарисовать плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета по исходным краям, получится 8 форм.

Однородные семиугольные/треугольные мозаики v т и
Symmetry: $[7,3], (*732)$							$[7,3] +, (732)$


${7,3}$	$t{7,3}$	$r{7,3}$	$t{3,7}$	${3,7}$	$rr{7,3}$	$tr{7,3}$	$sr{7,3}$
Uniform duals


$V7 3$	$V3.14.14$	$V3.7.3.7$	$V6.6.7$	$V3 7$	$V3.4.7.4$	$V4.6.14$	$V3.3.3.3.7$

См. также [ править ]

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б ( Рихтер ) Обратите внимание, что каждая грань многогранника состоит из нескольких граней мозаики — две треугольные грани составляют квадратную грань и так далее, как показано на поясняющем изображении .

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
Рихтер, Дэвид А., Как сделать группу Матье M ₂₄ , получено 15 апреля 2010 г.

Внешние ссылки [ править ]

[tiling-1] Перейти обратно: Перейти обратно: ^а ^б ( Рихтер ) Обратите внимание, что каждая грань многогранника состоит из нескольких граней мозаики — две треугольные грани составляют квадратную грань и так далее, как показано на поясняющем изображении .

[1]