Гептаграммная плитка порядка 7
 | Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( январь 2020 г. ) |
| Гептаграммная плитка порядка 7 | |
|---|---|
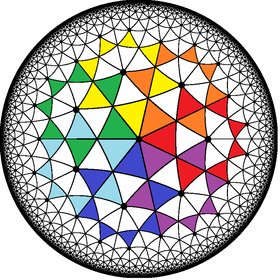 Модель диска Пуанкаре гиперболической плоскости | |
| Тип | Гиперболическая регулярная мозаика |
| Конфигурация вершин | (7/2) 7 |
| Символ Шлефли | {7/2,7} |
| Символ Витхоффа | 7 | 7/2 2 |
| Диаграмма Кокстера |      |
| Группа симметрии | [7,3], (*732) |
| Двойной | Семиугольная мозаика гептаграммного порядка |
| Характеристики | Вершинно-транзитивный , ребро-транзитивный , грани-транзитивный |
В геометрии представляет гептаграмматическое замощение 7-го порядка собой замощение гиперболической плоскости перекрывающимися гептаграммами .
Описание
[ редактировать ]Эта мозаика представляет собой обычную звездчатую мозаику и имеет символ Шлефли {7/2,7}. Гептаграммы, образующие мозаику, имеют тип {7/2}, 
. Перекрывающиеся гептаграммы делят гиперболическую плоскость на равнобедренные треугольники, 14 из которых образуют каждую гептаграмму.
Каждая точка гиперболической плоскости, не лежащая на ребре гептаграммы, принадлежит центральному семиугольнику одной гептаграммы и находится в одной из точек ровно одной другой гептаграммы. Число оборотов каждой гептаграммы вокруг своих точек равно единице, а число оборотов вокруг центрального семиугольника равно двум, поэтому, сложив эти два числа вместе, каждая точка плоскости будет окружена трижды; то есть плотность замощения равна 3.
В евклидовой плоскости гептаграмма типа {7/2} будет иметь углы в вершинах 3 π /7, но в гиперболической плоскости гептаграммы могут иметь более острый угол при вершине 2 π /7, который необходим для образования ровно семи других гептаграммы встречаются в центре каждой гептаграммы мозаики.
Связанные мозаики
[ редактировать ]Он имеет то же расположение вершин , что и обычная треугольная мозаика 7-го порядка , {3,7}. Полный набор ребер совпадает с ребрами семиугольной мозаики гептакиса . Вершины валентности 6 в этом мозаике являются ложными вершинами в гептаграммной , вызванной скрещенными ребрами.
Он связан с многогранником Кеплера-Пуансо , маленьким звездчатым додекаэдром {5/2,5}, который представляет собой многогранник и правильную звездчатую мозаику плотности -3 на сфере:
Ссылки
[ редактировать ]- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
См. также
[ редактировать ]
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
 | Эта гиперболической геометрии статья, посвященная , незавершена . Вы можете помочь Википедии, расширив ее . |