Сферический многогранник


В геометрии сферический многогранник или сферическая мозаика — это мозаика сферы , в которой поверхность разделена или разделена большими дугами на ограниченные области, называемые сферическими многоугольниками . Большую часть теории симметричных многогранников удобнее всего построить именно таким способом.
Самый известный сферический многогранник — это футбольный мяч , который рассматривается как сферический усеченный икосаэдр . Следующим по популярности сферическим многогранником является пляжный мяч , называемый осоэдром .
Некоторые «неправильные» многогранники, например осоэдры и их двойники , диэдры , существуют как сферические многогранники, но их плоскогранные аналоги вырождаются . Пример шестиугольного пляжного мяча: {2, 6} — это осоэдр, а {6, 2} — его двойной двугранник.
История
[ редактировать ]В 10 веке исламский ученый Абу аль-Вафа Бузджани (Абул Вафа) изучал сферические многогранники в рамках работы над геометрией, необходимой ремесленникам и архитекторам. [1]
Работа Бакминстера Фуллера о геодезических куполах в середине 20 века вызвала бум в изучении сферических многогранников. [2] Примерно в то же время Коксетер использовал их для перечисления всех однородных многогранников , кроме одного, посредством построения калейдоскопов ( конструкция Витхоффа ). [3]
Примеры
[ редактировать ]Все правильные многогранники , полуправильные многогранники и двойственные им многогранники можно спроецировать на сферу в виде мозаики:
| Шлефли символ | {п, д} | t{p,q} | г {р, q} | т{q,p} | {д, р} | rr{p,q} | tr{p,q} | ср{п,q} |
|---|---|---|---|---|---|---|---|---|
| Вертекс конфиг. | п д | q.2p.2p | pqpq | стр.2q.2q | д п | вопрос.4.п.4 | 4.2к.2п | 3.3.q.3.p |
| Тетраэдрический симметрия (3 3 2) |  3 3 |  3.6.6 |  3.3.3.3 |  3.6.6 |  3 3 |  3.4.3.4 |  4.6.6 |  3.3.3.3.3 |
 Версия 3.6.6 |  В3.3.3.3 |  Версия 3.6.6 |  Версия 3.4.3.4 |  Версия 4.6.6 |  В3.3.3.3.3 | |||
| Октаэдрический симметрия (4 3 2) |  4 3 |  3.8.8 |  3.4.3.4 |  4.6.6 |  3 4 |  3.4.4.4 |  4.6.8 |  3.3.3.3.4 |
 В3.8.8 |  Версия 3.4.3.4 |  Версия 4.6.6 |  Версия 3.4.4.4 |  Версия 4.6.8 |  В3.3.3.3.4 | |||
| икосаэдрический симметрия (5 3 2) |  5 3 |  3.10.10 |  3.5.3.5 |  5.6.6 |  3 5 |  3.4.5.4 |  4.6.10 |  3.3.3.3.5 |
 В3.10.10 |  В3.5.3.5 |  Версия 5.6.6 |  Версия 3.4.5.4 |  Версия 4.6.10 |  В3.3.3.3.5 | |||
| двугранный пример (р=6) (2 2 6) |  6 2 |  2.12.12 |  2.6.2.6 |  6.4.4 |  2 6 |  2.4.6.4 |  4.4.12 |  3.3.3.6 |

| н | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|
| н - Призма (2 2 р) |  |  |  |  |  |  | ... |
| n - Бипирамида (2 2 р) |  |  |  |  |  |  | ... |
| н - Антипризма |  |  |  | 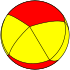 |  |  | ... |
| n - Трапецоэдр |  |  |  |  |  |  | ... |
Неподходящие случаи
[ редактировать ]Сферические мозаики допускают случаи, которых нет у многогранников, а именно: осоэдры : фигуры как {2,n} и диэдры : фигуры как {n,2}. Обычно используются правильные осоэдры и правильные диэдры.
| Космос | сферический | евклидов | |||||
|---|---|---|---|---|---|---|---|
| Укладка плитки имя | шестиугольный осоэдр | Дигональный осоэдр | Треугольный осоэдр | Квадрат осоэдр | пятиугольный осоэдр | ... | Апейрогональный осоэдр |
| Укладка плитки изображение |  | 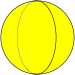 |  | 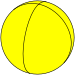 | 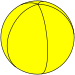 | ... | |
| Шлефли символ | {2,1} | {2,2} | {2,3} | {2,4} | {2,5} | ... | {2,∞} |
| Коксетер диаграмма | ... | ||||||
| Лица и края | 1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Вершины | 2 | 2 | 2 | 2 | 2 | ... | 2 |
| Вертекс конфиг. | 2 | 2.2 | 2 3 | 2 4 | 2 5 | ... | 2 ∞ |
| Космос | сферический | евклидов | |||||
|---|---|---|---|---|---|---|---|
| Укладка плитки имя | моногональный двугранник | Дигональный двугранник | Треугольный двугранник | Квадрат двугранник | пятиугольный двугранник | ... | Апейрогональный двугранник |
| Укладка плитки изображение | 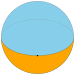 |  |  | 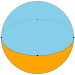 | 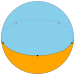 | ... | |
| Шлефли символ | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | ... | {∞,2} |
| Коксетер диаграмма | ... | ||||||
| Лица | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | ... | 2 {∞} |
| Края и вершины | 1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Вертекс конфиг. | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | ... | ∞.∞ |
Связь с мозаикой проективной плоскости
[ редактировать ]Сферические многогранники, имеющие хотя бы одну инверсную симметрию, относятся к проективным многогранникам. [4] (тесселяции реальной проективной плоскости ) - так же, как сфера имеет карту покрытия проективной плоскости 2 к 1, проективные многогранники соответствуют при 2-кратном покрытии сферическим многогранникам, которые симметричны при отражении через начало координат .
Наиболее известными примерами проективных многогранников являются правильные проективные многогранники, факторы центрально-симметричных платоновых тел , а также два бесконечных класса четных диэдров и осоэдров : [5]
- Полукуб , {4,3}/2
- Полуоктаэдр , {3,4}/2
- Полудодекаэдр , {5,3}/2
- Полуикосаэдр , {3,5}/2
- Полудиэдр, {2p,2}/2, p>=1
- Полуосоэдр, {2,2p}/2, p>=1
См. также
[ редактировать ]- Сферическая геометрия
- Сферическая тригонометрия
- Многогранник
- Проективный многогранник
- Тороидальный многогранник
- Обозначение многогранника Конвея
Ссылки
[ редактировать ]- ^ Сарханги, Реза (сентябрь 2008 г.). «Иллюстрируя Абу аль-Вафу Бузджани: плоские изображения, сферические конструкции». Иранские исследования . 41 (4): 511–523. дои : 10.1080/00210860802246184 .
- ^ Попко, Эдвард С. (2012). Разделенные сферы: геодезика и упорядоченное деление сферы . ЦРК Пресс. п. XIX. ISBN 978-1-4665-0430-1 .
Изобретение Бакминстером Фуллером геодезического купола стало самым большим стимулом для исследований и разработок сферических подразделений.
- ^ Коксетер, HSM ; Лонге-Хиггинс, MS ; Миллер, JCP (1954). «Равномерные многогранники». Фил. Транс . 246 А (916): 401–50. JSTOR 91532 .
- ^ МакМаллен, Питер ; Шульте, Эгон (2002). «6C. Проективные правильные многогранники». Абстрактные правильные многогранники . Издательство Кембриджского университета. стр. 162–5 . ISBN 0-521-81496-0 .
- ^ Коксетер, HSM (1969). «§21.3 Обычные карты ». Введение в геометрию (2-е изд.). Уайли. стр. 386–8 . ISBN 978-0-471-50458-0 . МР 0123930 .

