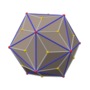
Пятиугольный икоситетраэдр

Пятиугольный икоситетраэдр
(Нажмите «Направо»* или «По часовой», чтобы вращать модели.)*
Тип	каталанский
Обозначение Конвея	ГК
Диаграмма Кокстера
Лицевой многоугольник	неправильный пятиугольник
Лица	24
Края	60
Вершины	38 = 6 + 8 + 24
Конфигурация лица	В3.3.3.3.4
Двугранный угол	136° 18' 33'
Группа симметрии	О , ½BC ₃ , [4,3] ⁺, 432
Двойной многогранник	курносый куб
Характеристики	выпуклый , гране-транзитивный , киральный
Сеть

Геометрическое построение постоянной Трибоначчи (AC) с циркулем и отмеченной линейкой в соответствии с методом, описанным Ксерардо Нейрой.

В геометрии — пятиугольный икоситетраэдр или пятиугольный икосикаитетраэдр. ^[1] — каталонское тело двойственное , курносому кубу . В кристаллографии его еще называют гироидом . ^[2]^[3]

Он имеет две различные формы, которые являются зеркальными отражениями (или « энантиоморфами ») друг друга.

Строительство [ править ]

Пятиугольный икоситетраэдр можно построить из курносого куба, не принимая двойственный куб. К шести квадратным граням курносого куба добавляются квадратные пирамиды, а к восьми треугольным граням, не имеющим общего ребра с квадратом, добавляются треугольные пирамиды. Высоты пирамид отрегулированы таким образом, чтобы они были копланарны другим 24 треугольным граням курносого куба. В результате получается пятиугольный икоситетраэдр.

Декартовы координаты [ править ]

Обозначим постоянную Трибоначчи через $t\approx 1.839\,286\,755\,21$ . ( см . в курносом кубе Геометрическое объяснение постоянной Трибоначчи .) Тогда декартовы координаты 38 вершин пятиугольного икоситетраэдра с центром в начале координат будут следующими:

12 четных перестановок ( $\pm1, \pm(2 t +1), \pm t 2)$ с четным количеством знаков минус
12 нечетных перестановок ( $\pm1, \pm(2 t +1), \pm t 2)$ с нечетным количеством знаков минус
6 баллов $(\pm t 3, 0, 0)$ , $(0, \pm t 3, 0)$ и $(0, 0, \pm t 3)$
8 баллов $(\pm t 2, \pm t 2, \pm t 2)$

Выпуклые оболочки этих вершин ^[4] масштабируется по $t^{-3}$ в результате получается октаэдр с единичным радиусом описанной окружности с центром в начале координат, единичный куб с центром в начале координат, масштабированный до $R\approx 0.9416969935$ и неправильный киральный курносый куб, масштабированный до $R$ , как показано на рисунке ниже:

Геометрия [ править ]

Пятиугольные грани имеют четыре угла. $\arccos((1-t)/2)\approx 114.812\,074\,477\,90^{\circ }$ и один угол $\arccos(2-t)\approx 80.751\,702\,088\,39^{\circ }$ . Пятиугольник имеет три коротких ребра единичной длины каждое и два длинных ребра длины. $(t+1)/2\approx 1.419\,643\,377\,607\,08$ . Острый угол находится между двумя длинными краями. Двугранный угол равен $\arccos(-1/(t^{2}-2))\approx 136.309\,232\,892\,32^{\circ }$ .

Если его двойной курносый куб имеет единичную длину ребра, его площадь поверхности и объем равны: ^[5]

{\begin{aligned}A&=3{\sqrt {\frac {22(5t-1)}{4t-3}}}&&\approx 19.299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)}}}&&\approx 7.4474\end{aligned}}

Ортогональные проекции [ править ]

Пятиугольный икоситетраэдр имеет три позиции симметрии: две с центрами по вершинам и одну по середине.

Ортогональные проекции
Проективный симметрия	[3]	[4] ⁺	[2]
Изображение
Двойной изображение

Вариации [ править ]

Изоэдрические вариации с той же кирально-октаэдрической симметрией могут быть построены с пятиугольными гранями, имеющими 3 длины ребра.

Этот показанный вариант можно построить путем добавления пирамид к 6 квадратным граням и 8 треугольным граням курносого куба, так что новые треугольные грани с тремя копланарными треугольниками сливаются в идентичные грани пятиугольника.

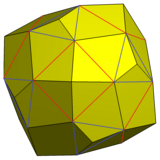Курносый куб с увеличенными пирамидами и слитыми гранями	Пятиугольный икоситетраэдр	Сеть

Связанные многогранники и мозаики [ править ]

Этот многогранник топологически связан как часть последовательности многогранников и замощений пятиугольников с конфигурациями граней (V3.3.3.3.n ) . (Последовательность переходит в мозаику гиперболической плоскости до любого n .) Эти гране-транзитивные фигуры обладают (n32) вращательной симметрией .

n 32 мутации симметрии курносых мозаик: 3.3.3.3.n v т и
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
Symmetry n32	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Пятиугольный икоситетраэдр является вторым в ряду двойственно курносых многогранников и мозаик с конфигурацией граней V3.3.4.3. н .

4 n 2 мутации симметрии курносых мозаик: 3.3.4.3.n v т и
Symmetry 4n2	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry 4n2	242	342	442	542	642	742	842	∞42
Snub figures
Config.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Gyro figures
Config.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Пятиугольный икоситетраэдр — один из семейства двойственных однородных многогранников, родственных кубу и правильному октаэдру.

Однородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Ссылки [ править ]

^ Конвей, Симметрии вещей, стр.284.
^ «Проморфология кристаллов I» .
^ «Кристаллическая форма, зоны и привычки» . Архивировано из оригинала 23 августа 2003 г.
^ Коджа, Мехмет; Оздеш Коджа, Назифе; Коч, Рамазон (2010). «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов». Журнал математической физики . 51 (4). arXiv : 0908.3272 . дои : 10.1063/1.3356985 .
^ Вайсштейн, Эрик В. , « Пятиугольный икоситетраэдр » (« каталонское тело ») в MathWorld .

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им многогранники, стр. 28, Пятиугольный икоситетраэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , ISBN 978-1-56881-220-5 [1] (Глава 21, Названия архимедовых и каталонских многогранников и мозаик, страница 287, пятиугольный икосикаитетраэдр)

Внешние ссылки [ править ]

Пятиугольный икоситетраэдр – интерактивная модель многогранника

[1] Конвей, Симметрии вещей, стр.284.

[2] «Проморфология кристаллов I» .

[3] «Кристаллическая форма, зоны и привычки» . Архивировано из оригинала 23 августа 2003 г.

[4] Коджа, Мехмет; Оздеш Коджа, Назифе; Коч, Рамазон (2010). «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов». Журнал математической физики . 51 (4). arXiv : 0908.3272 . дои : 10.1063/1.3356985 .

[5] Вайсштейн, Эрик В. , « Пятиугольный икоситетраэдр » (« каталонское тело ») в MathWorld .

[1]

[2]

[3]

[4]

[5]