Курносая четырехпентагональная черепица

Курносая четырехпентагональная черепица
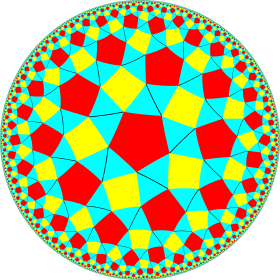Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая равномерная мозаика
Конфигурация вершин	3.3.4.3.5
Символ Шлефли	ср{5,4} или $s{\begin{Bmatrix}5\\4\end{Bmatrix}}$
Символ Витхоффа	\| 5 4 2
Диаграмма Кокстера	или
Группа симметрии	[5,4] ⁺, (542)
Двойной	Пятиугольная плитка Order-5-4 цветочка
Характеристики	Вершинно-транзитивный хиральный

В геометрии курносая тетрапентагональная мозаика является однородной мозаикой гиперболической плоскости . Он имеет символ Шлефли sr{5,4}.

Изображения

Нарисовано киральными парами, без краев между черными треугольниками:

Двойной элемент называется пятиугольной мозаикой цветочков порядка 5-4 и определяется конфигурацией грани V3.3.4.3.5.

Плосконосая тетрапентагональная мозаика является четвертой в серии курносых многогранников и мозаик с фигурой вершины 3.3.4.3. н .

4 n 2 мутации симметрии курносых мозаик: 3.3.4.3.n v т и
Symmetry 4n2	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry 4n2	242	342	442	542	642	742	842	∞42
Snub figures
Config.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Gyro figures
Config.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Однородные пятиугольные/квадратные плитки v т и
Symmetry: [5,4], (*542)							[5,4]⁺, (542)	[5⁺,4], (5*2)	[5,4,1⁺], (*552)


{5,4}	t{5,4}	r{5,4}	2t{5,4}=t{4,5}	2r{5,4}={4,5}	rr{5,4}	tr{5,4}	sr{5,4}	s{5,4}	h{4,5}
Uniform duals


V5⁴	V4.10.10	V4.5.4.5	V5.8.8	V4⁵	V4.4.5.4	V4.8.10	V3.3.4.3.5	V3.3.5.3.5	V5⁵

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .