Гирих Плитка
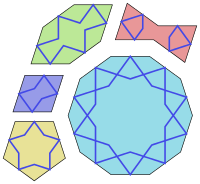
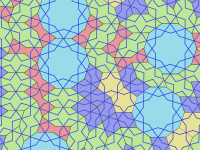
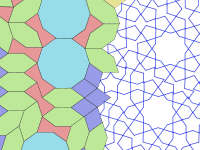
Гирих Плитки представляют собой набор из пяти плиток , которые использовались при создании исламских геометрических узоров с использованием ремешков ( гирих ) для украшения зданий в исламской архитектуре . Они использовались примерно с 1200 года, и их устройство значительно улучшилось, начиная с храма Дарби Имама в Исфахане в Иране, построенного в 1453 году.
Пять плиток [ править ]
Пять форм плиток и их персидские названия: [1]
| Имя | Персидское имя | количество углов | выпуклый | характеристики угла |
|---|---|---|---|---|
| правильный десятиугольник | Стол | 10 | да | 144° |
| вытянутый (неправильный выпуклый) шестиугольник | Шеш Банд | 6 | да | [ 72°, 144°, 144° ] ×2 |
| галстук-бабочка (невыпуклый шестигранник) | Сорме Дэн | 6 | нет | [ 72°, 72°, 216° ] ×2 |
| ромб | Торанж | 4 | да | [ 72°, 108° ] ×2 |
| правильный пятиугольник | Помещать | 5 | да | 108° |
Все стороны этих фигур имеют одинаковую длину, а все их углы кратны 36° (π/5 радиан ). Все они, кроме пятиугольника, обладают двусторонней (отражательной) симметрией через две перпендикулярные линии. Некоторые имеют дополнительную симметрию. В частности, десятиугольник имеет десятикратную вращательную симметрию (поворот на 36 °); а пятиугольник имеет пятикратную вращательную симметрию (поворот на 72 °).
Появление плиток гирих [ править ]
К концу 11 века исламские художники Северной Африки начали использовать « плиточную мозаику », которая является предшественницей мозаики . [2] К 13 веку ислам открыл новый способ построения «плиточной мозаики» благодаря развитию арифметических вычислений и геометрии — плитки гирих. [3]
Гирих [ править ]
Гирих — это линии ( ремешки ), украшающие плитку. Плитки используются для формирования узоров гирих, от персидского слова گره , что означает «узел». [4] В большинстве случаев видны только гирих (и другие мелкие украшения, такие как цветы), а не границы самих плиток. Гири — это кусочные прямые линии, пересекающие границы плиток в центре края под углом 54 ° (3π/10 радиан) к краю. Два пересекающихся гирих пересекают каждый край плитки. Большинство плиток имеют уникальный рисунок гирих внутри плитки, который является непрерывным и повторяет симметрию плитки. Однако в десятиугольнике есть два возможных образца гирих, один из которых имеет только пятикратную, а не десятикратную вращательную симметрию.
Математика мозаики гирих [ править ]
В 2007 году физики Питер Дж. Лу и Пол Дж. Стейнхардт предположили, что мозаики гирих обладают свойствами, согласующимися с самоподобными фрактальными квазикристаллическими мозаиками, такими как плитки Пенроуза , предшествовавшими им на пять столетий. [5] [6]
Этот вывод был подтвержден как анализом узоров на сохранившихся сооружениях, так и изучением персидских свитков XV века. Нет никаких указаний на то, насколько больше архитекторы могли знать о задействованной математике. Принято считать, что такие конструкции создавались путем рисования зигзагообразных контуров с помощью только линейки и циркуля. длиной 97 футов (29,5 метров) шаблоны, найденные на свитках, таких как свиток Топкапы Возможно, использовались . На свитке , найденном во дворце Топкапы в Стамбуле, административном центре Османской империи, и предположительно датируемом концом 15 века, изображена последовательность двух- и трехмерных геометрических узоров. Текста нет, но есть сетка и цветовая кодировка, используемая для выделения симметрии и различения трехмерных проекций. Рисунки, подобные показанным на этом свитке, служили книгами с выкройками для мастеров, изготавливавших плитки, а форма плиток гирих определяла, как их можно было комбинировать в большие узоры. Таким образом, мастера могли создавать очень сложные конструкции, не прибегая к математике и не обязательно понимая их основные принципы. [7]
Такое использование повторяющихся узоров, созданных из ограниченного числа геометрических фигур, доступных мастерам того времени, похоже на практику современных европейских готических мастеров. Дизайнеры обоих стилей стремились использовать свой набор геометрических фигур для создания максимального разнообразия форм. Это требовало навыков и практики, сильно отличающихся от математики. [7]
мозаики из декаграмм Геометрическое построение взаимосвязанной и многоугольников
Сначала разделите прямой угол А на пять частей одинаковой степени, создав четыре луча, начинающихся из А. Найдите на втором луче произвольную точку С и опустите перпендикуляры из С к сторонам угла А против часовой стрелки. На этом этапе создается прямоугольник ABCD вместе с четырьмя сегментами, каждый из которых имеет конечную точку A; другие конечные точки — это пересечения четырех лучей с двумя сторонами BC и DC прямоугольника ABCD. Затем найдите середину четвертого сегмента, созданного из точки E четвертого луча. Постройте дугу с центром A и радиусом AE, пересекающую AB в точке F и второй луч в точке G. Второй сегмент теперь является частью прямоугольника. диагональ. Проведите прямую, параллельную AD и проходящую через точку G, которая пересекает первый луч в точке H и третий луч в точке I. Прямая HF проходит через точку E и пересекает третий луч в точке L и линию AD в точке J. Постройте прямую проходя через точку J, параллельную третьему лучу. Также постройте линию EI и найдите M, которая является пересечением этой линии с AD. Из точки F проведите линию, параллельную третьему лучу, до пересечения с первым лучом в точке K. Постройте отрезки GK, GL и EM. Найдите точку N такую, что GI = IN, построив окружность с центром I и радиусом IG. Постройте линию DN, параллельную GK, пересекающую линию, исходящую из J, и найдите P, чтобы завершить правильный пятиугольник EINPJ. Линия DN пересекает серединный перпендикуляр к AB в точке Q. Из Q постройте линию, параллельную FK, чтобы пересечь луч MI в точке R. Как показано на рисунке, используйте O, которая является центром прямоугольника ABCD, в качестве центра поворота на 180 °. , можно создать фундаментальную область для замощения. [1]




построение мозаики из архитектурных свитков Геометрическое Мирзы Акбара
Сначала разделите прямой угол на пять равных углов. На первом луче против часовой стрелки выбирается произвольная точка P. В качестве радиуса круга, вписанного в декаграмму, выбрана половина отрезка, созданного из третьего луча, отрезка АМ. Следующий рисунок иллюстрирует пошаговое наглядное решение задачи автором циркуля-линейки. [1] Обратите внимание, что способ разделения прямого угла на пять равных углов не входит в представленные инструкции, поскольку считается элементарным шагом для дизайнеров.

Примеры [ править ]
- Различные узоры
- Окно квартиры наследного принца во дворце Топкапы , Стамбул , Турция, с 6-балльными звездами; окружающая среда выложена цветочной арабеской
- Внутренняя арка при открытии ложи султана в Османской зеленой мечети в Бурсе , Турция (1424 г.), с 10-конечными звездами и пятиугольниками.
- Деревянная ширма из Нишапура . караван-сарая
Гирих широко применялся в архитектуре. Гирих на персидских геометрических окнах отвечает требованиям персидской архитектуры. Конкретные типы украшений, используемые в ороси, обычно связывали окна с социальным и политическим авторитетом покровителя. Чем более богато украшено окно, тем более высокий социальный и экономический статус имеет его владелец. Хорошим примером этого является Азад Колиджи, сад Довлатабад в Иране. [ нужна ссылка ] . Узоры гирих на его окне удачно демонстрируют многослойность. Первым слоем будет настоящий сад, который люди смогут увидеть, открыв окно. Затем на внешней стороне окна появляется первый узор гирих, резной узор. Еще одним искусственным слоем является разноцветное оконное стекло, разноцветные слои которого создают ощущение массы цветов. Этот абстрактный слой образует явное противоречие с реальным слоем за окном и дает простор для фантазии. [8]
См. также [ править ]
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с Сарханги, Реза (2012). «Переплетающиеся звездные многоугольники в персидской архитектуре: особый случай декаграммы в мозаичном дизайне». Нексус Сеть Дж . 14 (2). п. 350. дои : 10.1007/s00004-012-0117-5 . S2CID 253596464 .
- ^ Хаттштейн /Делиус., Маркус/Питер (2013). Ислам: искусство и архитектура . Потсдам: Х.Ф. Ульманн. п. 448. ИСБН 978-3848003808 .
- ^ Лу, Пи Джей; Стейнхардт, П.Дж. (2007). «Декагональные и квазикристаллические плитки в средневековой исламской архитектуре». Наука . 315 (5815): 1106–1110. Бибкод : 2007Sci...315.1106L . дои : 10.1126/science.1135491 . JSTOR 20039057 . ПМИД 17322056 . S2CID 10374218 .
- ^ Себастьян Р. Прейндж (сентябрь – октябрь 2009 г.). «Плитки бесконечности» . Saudi Aramco World : 24–31. Архивировано из оригинала 13 января 2010 г. Проверено 8 января 2010 г.
- ^ Питер Дж. Лу и Пол Дж. Стейнхардт (2007). «Декагональные и квазикристаллические плитки в средневековой исламской архитектуре». Наука . 315 (5815): 1106–1110. Бибкод : 2007Sci...315.1106L . дои : 10.1126/science.1135491 . ПМИД 17322056 . S2CID 10374218 .
- ^ Дополнительные цифры
- ↑ Перейти обратно: Перейти обратно: а б Гулру Неджипоглу (1995). Свиток Топкапы: геометрия и орнамент в исламской архитектуре . Исследовательский институт Гетти.
- ^ Колиджи, Хуман (2015). «Построенный на свете: «хитрое» искусство окон с геометрическим узором» . Международный журнал исламской архитектуры . 4 : 75–108. дои : 10.1007/s00004-016-0288-6 .
Внешние ссылки [ править ]
- Узоры в арабской архитектуре
- «Средневековая исламская архитектура предвещает математику 20-го века» . Вестник Гарвардского университета. 22 февраля 2007 г. Проверено 14 марта 2007 г.
- «Средневековая исламская плитка демонстрирует математическую смекалку» . Новый учёный. 22 февраля 2007 г. Проверено 14 марта 2007 г.






