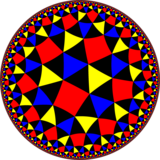
Треугольная плитка курносого порядка 8
| Треугольная плитка курносого порядка 8 | |
|---|---|
 Модель диска Пуанкаре гиперболической плоскости | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершин | 3.3.3.3.3.4 |
| Символ Шлефли | с{3,8} с(4,3,3) |
| Символ Витхоффа | | 4 3 3 |
| Диаграмма Кокстера | |
| Группа симметрии | [8,3 + ], (3*4) [(4,3,3)] + , (433) |
| Двойной | Плоская двойная плитка Order-4-3-3 |
| Характеристики | Вершинно-транзитивный |
В геометрии курносая тритетратригональная мозаика или курносая треугольная мозаика восьмого порядка является однородной мозаикой гиперболической плоскости . Он имеет символы Шлефли s{(3,4,3)} и s{3,8}.
Изображения
[ редактировать ]Нарисовано в киральных парах:
Симметрия
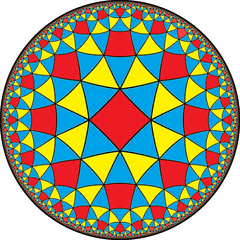
[ редактировать ]Альтернативная имеет конструкция из усеченной треугольной мозаики 8-го порядка треугольники двух цветов и ахиральную симметрию. Он имеет символ Шлефли s{3,8}.
Связанные многогранники и мозаика
[ редактировать ]| Симметрия: [(4,3,3)], (*433) | [(4,3,3)] + , (433) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  | |||
| ч{8,3} т 0 (4,3,3) | г{3,8} 1 / 2 т 0,1 (4.3.3) | ч{8,3} т 1 (4,3,3) | ч 2 {8,3} т 1,2 (4,3,3) | {3,8} 1 / 2 т 2 (4,3,3) | ч 2 {8,3} т 0,2 (4.3.3) | т{3,8} 1 / 2 т 0,1,2 (4,3,3) | с{3,8} 1 / 2 с(4,3,3) | |||
| Униформа дуалы | ||||||||||
 |  |  |  |  |  |  |  | |||
| V(3.4) 3 | В3.8.3.8 | V(3.4) 3 | Версия 3.6.4.6 | V(3.3) 4 | Версия 3.6.4.6 | Версия 6.6.8 | В3.3.3.3.3.4 | |||
| Однородные восьмиугольные/треугольные плитки |
|---|
Ссылки
[ редактировать ]- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
См. также
[ редактировать ]Викискладе есть медиафайлы, связанные с унифицированной мозаикой 3-3-3-3-3-4 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
- Галерея гиперболических и сферических плиток
- KaleidoTile 3: образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик.
- Гиперболические плоские мозаики, Дон Хэтч