Усеченная триоктагональная плитка

Усеченная триоктагональная плитка
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая равномерная мозаика
Конфигурация вершин	4.6.16
Символ Шлефли	tr{8,3} или $t{\begin{Bmatrix}8\\3\end{Bmatrix}}$
Символ Витхоффа	2 8 3 |
Диаграмма Кокстера	или
Группа симметрии	[8,3], (*832)
Двойной	Заказать 3-8 кисромбиллей
Характеристики	Вершинно-транзитивный

В геометрии представляет усеченная триоктагональная мозаика собой полуправильную мозаику гиперболической плоскости. есть один квадрат , один шестиугольник и один шестиугольник (16 сторон) В каждой вершине . имеет символ Шлефли tr Он {8,3}.

Симметрия

Усеченная триоктагональная плитка с зеркальными линиями

Двойственный этому мозаике, киромбилл порядка 3-8 , представляет фундаментальные области симметрии [8,3] (*832). Имеются 3 небольшие индексные подгруппы, построенные из [8,3] путем удаления и чередования зеркал. В этих изображениях фундаментальные области попеременно окрашены в черный и белый цвета, а на границах между цветами существуют зеркала.

Большая подгруппа индекса 6, построенная как [8,3 ^* ], становится [(4,4,4)], (*444). Промежуточная подгруппа индекса 3 строится как [8,3 ^⅄ ], удалены 2/3 синих зеркал.

Малые индексные подгруппы из [8,3], (*832)

Индекс	1	2		3	6
Диаграммы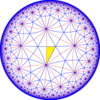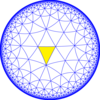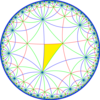
Коксетер ( орбифолд )	[8,3] = (*832)	[1 + ,8,3] = = ( *433 )	[8,3 + ] = (3*4)	[8,3 ⅄ ] = = ( *842 )	[8,3 * ] = = ( *444 )
Прямые подгруппы
Индекс	2	4		6	12
Диаграммы
Коксетер (орбифолд)	[8,3] + = (832)	[8,3 + ] + = = (433)		[8,3 ⅄ ] + = = (842)	[8,3 * ] + = = (444)

Заказать 3-8 кисромбиллей

Усеченная триоктагональная плитка
Тип	Двойная полуправильная гиперболическая мозаика
Лица	Прямоугольный треугольник
Края	бесконечный
Вершины	бесконечный
Диаграмма Кокстера
Группа симметрии	[8,3], (*832)
Группа вращения	[8,3] + , (832)
Двойной многогранник	Усеченная триоктагональная плитка
Конфигурация лица	В4.6.16
Характеристики	лице-переходный

представляет Киромбилль порядка 3–8 собой полуправильное двойственное замощение гиперболической плоскости . Он состоит из конгруэнтных прямоугольных треугольников которых сходятся 4, 6 и 16 треугольников , в каждой вершине .

На изображении показана проекция модели диска Пуанкаре на гиперболическую плоскость.

Он помечен как V4.6.16, потому что каждая грань прямоугольного треугольника имеет три типа вершин: одна с 4 треугольниками, одна с 6 треугольниками и одна с 16 треугольниками. Это двойная мозаика усеченной триоктагональной мозаики, в каждой вершине которой есть один квадрат, один восьмиугольник и один шестиугольник.

Мы

Альтернативное название - киромбилль Конвея kis , рассматривающее его как ромбическую мозаику 3-8, разделенную оператором 3-8 , добавляющую центральную точку к каждому ромбу и разделяющую на четыре треугольника.

Связанные многогранники и мозаики

Это разбиение является одним из 10 однородных разбиений, построенных на основе [8,3] гиперболической симметрии и трех подсимметрий [1 ⁺ ,8,3], [8,3 ⁺ ] и [8,3] ⁺ .

показывать Однородные восьмиугольные/треугольные плитки
Symmetry: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								or	or
Uniform duals
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

Эту мозаику можно считать членом последовательности однородных шаблонов с фигурой вершины (4.6.2p) и диаграммой Коксетера-Динкина. . Для p < 6 членами последовательности являются всеусеченные многогранники ( зоноэдры ), показанные ниже в виде сферических мозаик. При p > 6 они представляют собой мозаику гиперболической плоскости, начиная с усеченной тригептагональной мозаики .

показывать * n 32 мутация симметрии всеусеченных мозаик: 4.6.2n
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

См. также

• Замощения правильных многоугольников
• Треугольная мозаика Гексакиса
• Список однородных мозаик
• Равномерные мозаики в гиперболической плоскости

Ссылки

• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN   978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
• «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN  0-486-40919-8 . LCCN   99035678 .

Внешние ссылки

• Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
• Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
• Галерея гиперболических и сферических плиток
• KaleidoTile 3: образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик.
• Гиперболические плоские мозаики, Дон Хэтч