Обозначение многогранника Конвея

В геометрии и топологии , основанных на исходном многограннике , нотация многогранника Конвея , изобретенная Джоном Хортоном Конвеем и продвигаемая Джорджем Хартом , используется для описания многогранников модифицированном различными префиксными операциями . ^[1]^[2]

Конвей и Харт расширили идею использования операторов, таких как усечение , определенное Кеплером , для построения связанных многогранников одинаковой симметрии. Например, $tC$ представляет собой усеченный куб , а $taC$ , анализируемый как $t (aC)$ , является ( топологически ) усеченным кубооктаэдром . Простейший оператор двойного обмена местами элементов вершин и граней ; двойственный куб — это октаэдр : $dC = O.$ например , При последовательном применении эти операторы позволяют множество многогранников более высокого порядка генерировать . Конвей определил операторы $a$ (амбо), $b$ ( фаска ), $d$ ( двойной ), $e$ (расширение), $g$ (гироскоп), $j$ (соединение), $k$ (кис), $m$ (мета), $o$ (орто), $s$ ( snub ) и $t$ ( truncate ), а Харт добавил $r$ ( Reflection ) и $p$ (пропеллер). ^[3] В более поздних реализациях были названы дополнительные операторы, иногда называемые «расширенными» операторами. ^[4]^[5] Базовых операций Конвея достаточно для создания архимедовых и каталонских тел из платоновых тел . Некоторые базовые операции могут быть выполнены как составные части других: например, дважды примененная ambo — это операция расширения ( $aa = e$ ), а усечение после ambo создает скос ( $ta = b$ ).

Многогранники можно изучать топологически, с точки зрения того, как их вершины, ребра и грани соединяются друг с другом, или геометрически, с точки зрения размещения этих элементов в пространстве. Различные реализации этих операторов могут создавать многогранники, геометрически разные, но топологически эквивалентные. Эти топологически эквивалентные многогранники можно рассматривать как одно из многих вложений на многогранного графа сфере. Если не указано иное, в этой статье (и в литературе по операторам Конвея в целом) топология является основной задачей. Многогранники рода 0 (т.е. топологически эквивалентные сфере) часто приводятся в каноническую форму, чтобы избежать двусмысленности.

Операторы

В обозначениях Конвея операции над многогранниками применяются как функции, справа налево. Например, кубооктаэдр — это куб амбо , ^[6] то есть ⁠ $a(C)=aC$ ⁠ , а усечённый кубооктаэдр — это ⁠ $t(a(C))=t(aC)=taC$ ⁠ . Повторное применение оператора можно обозначить показателем степени: j ² = о . В общем, операторы Конвея некоммутативны .

Отдельные операторы можно визуализировать с точки зрения фундаментальных областей (или камер), как показано ниже. Каждый прямоугольный треугольник является фундаментальной областью . Каждая белая камера представляет собой повернутую версию остальных, как и каждая цветная камера. Для ахиральных операторов цветные камеры являются отражением белых камер, и все они транзитивны. В групповых терминах ахиральные операторы соответствуют группам диэдра $D n$ , где n — количество сторон грани, а киральные операторы соответствуют циклическим группам $C n,$ лишенным отражательной симметрии групп диэдра. Ахиральные и киральные операторы также называются локальными операциями, сохраняющими симметрию (LSP) и локальными операциями, сохраняющими симметрию, сохраняющую ориентацию (LOPSP) соответственно. ^[7]^[8]^[9]LSP следует понимать как локальные операции, сохраняющие симметрию, а не операции, сохраняющие локальную симметрию. Опять же, это симметрии в топологическом, а не геометрическом смысле: точные углы и длины ребер могут различаться.

Основные области лиц с $n$ стороны
3 (Треугольник)	4 (Квадрат)	5 (Пентагон)	6 (Шестиугольник)

Фундаментальные области для групп многогранников. Группы $D_{3},D_{4},D_{5},D_{6}$ для ахиральных многогранников и $C_{3},C_{4},C_{5},C_{6}$ для киральных многогранников.

Харт ввел оператор отражения r , который дает зеркальное отображение многогранника. ^[6] Это не строго LOPSP, поскольку он не сохраняет ориентацию: он меняет ее, меняя местами белые и красные камеры. r не влияет на ахиральные многогранники, кроме ориентации, а rr = S возвращает исходный многогранник. Перечеркивание может использоваться для обозначения другой киральной формы оператора: s = rsr .

Операция неприводима, если ее нельзя выразить в виде композиции операторов, кроме d и r . Большинство исходных операторов Конвея неприводимы: исключениями являются e , b , o и m .

Матричное представление

х	${\begin{bmatrix}a&b&c\\0&d&0\\a'&b'&c'\end{bmatrix}}=\mathbf {M} _{x}$
хд	${\begin{bmatrix}c&b&a\\0&d&0\\c'&b'&a'\end{bmatrix}}=\mathbf {M} _{x}\mathbf {M} _{d}$
дх	${\begin{bmatrix}a'&b'&c'\\0&d&0\\a&b&c\end{bmatrix}}=\mathbf {M} _{d}\mathbf {M} _{x}$
dxd	${\begin{bmatrix}c'&b'&a'\\0&d&0\\c&b&a\end{bmatrix}}=\mathbf {M} _{d}\mathbf {M} _{x}\mathbf {M} _{d}$

Связь между количеством вершин, ребер и граней семени и многогранника, созданного операциями, перечисленными в этой статье, может быть выражена в виде матрицы. $\mathbf {M} _{x}$ . Когда x является оператором, $v,e,f$ являются вершинами, ребрами и гранями семени (соответственно), а $v',e',f'$ являются вершинами, ребрами и гранями результата, тогда

\mathbf {M} _{x}{\begin{bmatrix}v\\e\\f\end{bmatrix}}={\begin{bmatrix}v'\\e'\\f'\end{bmatrix}}

.

Матрица композиции двух операторов — это просто произведение матриц этих двух операторов. Различные операторы могут иметь одну и ту же матрицу, например, p и l . Количество ребер результата представляет собой целое число d, кратное значению начального числа: это называется уровнем инфляции или краевым фактором. ^[7]

Простейшие операторы, тождественный оператор S и двойственный оператор d , имеют простые матричные формы:

\mathbf {M} _{S}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}=\mathbf {I} _{3}

,

\mathbf {M} _{d}={\begin{bmatrix}0&0&1\\0&1&0\\1&0&0\end{bmatrix}}

Два двойных оператора сокращаются; dd = S и квадрат $\mathbf {M} _{d}$ является единичной матрицей . Применительно к другим операторам двойственный оператор соответствует горизонтальному и вертикальному отражению матрицы. Операторы могут быть сгруппированы в группы по четыре человека (или меньше, если некоторые формы одинаковы), идентифицируя операторы x , xd (оператор двойственного оператора), dx (двойственный оператор) и dxd (сопряженный оператор). В этой статье дана только матрица для x , поскольку остальные являются простыми отражениями.

Количество операторов

Число LSP для каждого уровня инфляции равно $2,2,4,6,6,20,28,58,82,\cdots$ начиная с уровня инфляции 1. Однако не все LSP обязательно создают многогранник, ребра и вершины которого образуют 3-связный граф , и, как следствие теоремы Стейница, не обязательно создают выпуклый многогранник из выпуклого семени. Число 3-связных LSP для каждого уровня инфляции равно $2,2,4,6,4,20,20,54,64,\cdots$ . ^[8]

Оригинальные операции

Строго говоря, семя ( S ), игла ( n ) и zip ( z ) не были включены Конвеем, но они связаны с исходными операциями Конвея двойственностью, поэтому включены сюда.

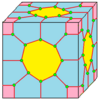
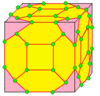
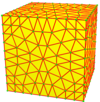
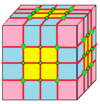
С этого момента операции визуализируются на семенах куба, нарисованных на поверхности этого куба. Синие грани пересекают края семени, а розовые грани лежат над вершинами семени. Существует некоторая гибкость в точном размещении вершин, особенно при использовании киральных операторов.

Оригинальные операторы Конвея
Краевой фактор	Матрица $\mathbf {M} _{x}$	х	хд	дх	dxd	Примечания
1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$	Семя : С	Двойной : д		Начальное значение : дд = S	Dual заменяет каждую грань вершиной, а каждую вершину гранью.
2	${\begin{bmatrix}1&0&1\\0&2&0\\0&1&0\end{bmatrix}}$	Присоединяйтесь : j		Вверху : а		Соединение создает четырехугольные грани. Амбо создает вершины степени 4 и также называется выпрямлением или срединным графом в теории графов. ^[10]
3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$	Маленький : к	Игла : н	Почтовый индекс : z	Усечь : т	Кис воздвигает пирамиду на каждой грани, и его еще называют акизация, Клитопа , кумуляция, ^[11] аккреция, или увеличение пирамиды . Усечение обрезает многогранник по его вершинам, но оставляет часть исходных ребер. ^[12] Zip также называют битранцией .
4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$	Орто : о = jj		Развернуть : е = аа
5	${\begin{bmatrix}1&2&1\\0&5&0\\0&2&0\end{bmatrix}}$	Гироскоп : г	гд = ггр	сд = рср	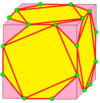Пренебрежение : с	Киральные операторы. См. Snub (геометрия) . В отличие от Харта, ^[3] gd — это не то же самое, что g : это его киральная пара. ^[13]
6	${\begin{bmatrix}1&1&1\\0&6&0\\0&4&0\end{bmatrix}}$	Мета : м = кДж		Фаска : b = ta

Семена

Затравкой может служить любой многогранник, если над ним можно выполнять операции. Обычным семенам присвоена буква.Платоновы тела обозначаются первой буквой Тетраэдр I , Октаэдр Додекаэдр , Куб ) , , косаэдр ; ( своего названия призмы ( ) ; Pn _{- угольных} для n форм а нтипризмы ( Ан ₎ ; c u polae ( Un ₎ ; антикуполы ( V _n ); и пирамиды ) ( Y _n . Любое можно твердое тело Джонсона обозначить как J _n для n = 1..92.

Все пять платоновых тел могут быть созданы с помощью призматических генераторов с использованием от нуля до двух операторов: ^[14]

Треугольная пирамида : Y ₃ (Тетраэдр – особая пирамида)
- Т = Y ₃
- O = aT (оба тетраэдра)
- C = jT (объединить тетраэдр)
- I = sT (плосконосый тетраэдр)
- D = gT (гиротетраэдр)
Треугольная антипризма : А ₃ (Октаэдр — особая антипризма)
- О = _А3
- С = дА ₃
Квадратная призма : P ₄ (Куб — особая призма)
- С = П ₄
Пятиугольная : А5 _{антипризма}
- I = k ₅ A ₅ (Особая гироудлиненная дипирамида )
- D = t ₅ dA ₅ (Особый усеченный трапецоэдр )

Обычные евклидовы мозаики также можно использовать в качестве затравок:

Q = Кадриль = Квадратная мозаика
H = шестиугольник = шестиугольная мозаика = dΔ
Δ = Дельтиль = Треугольная мозаика = dH

Расширенные операции

Это операции, созданные на основе исходного набора Конвея. Обратите внимание, что существует гораздо больше операций, чем было названо; то, что операции здесь нет, не означает, что она не существует (или не является LSP или LOPSP). Для упрощения можно сказать, что только неприводимые операторывключены в этот список: другие могут быть созданы путем составления операторов вместе.

Неприводимые расширенные операторы
Краевой фактор	Матрица $\mathbf {M} _{x}$	х	хд	дх	dxd	Примечания
4	${\begin{bmatrix}1&2&0\\0&4&0\\0&1&1\end{bmatrix}}$	Фаска : c	компакт-диск = ты	постоянный ток = выход	Разделить : ты	Chamfer — это форма соединения l . См. Фаска (геометрия) .
5	${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$	Пропеллер : р	дп = пд		дпд = п	Киральные операторы. Оператор пропеллера был разработан Джорджем Хартом. ^[15]
5	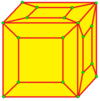${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$	лофт : л	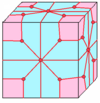лд	дл	длд
6	${\begin{bmatrix}1&3&0\\0&6&0\\0&2&1\end{bmatrix}}$	Квинто : Вопрос	qd	дк	dqd
6	${\begin{bmatrix}1&2&0\\0&6&0\\0&3&1\end{bmatrix}}$	Соединение шнурка : L ₀	Л ₀ д	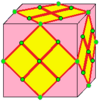дл ₀	дл ₀ д	См. ниже объяснение обозначений соединения.
7	${\begin{bmatrix}1&2&0\\0&7&0\\0&4&1\end{bmatrix}}$	Кружево : L	Лд	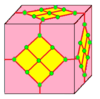дл	длд
7	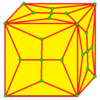${\begin{bmatrix}1&2&1\\0&7&0\\0&4&0\end{bmatrix}}$	Ставка : К	Кд	дК	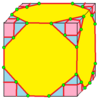дКд
7	${\begin{bmatrix}1&4&0\\0&7&0\\0&2&1\end{bmatrix}}$	Вихрь : ш	вд = дв	v = dw	Волюта : v	Киральные операторы.
8	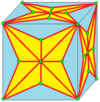${\begin{bmatrix}1&2&1\\0&8&0\\0&5&0\end{bmatrix}}$	Присоединяйтесь-кис-кис : ⁠ $(kk)_{0}$ ⁠	⁠ $(kk)_{0}d$ ⁠	⁠ $d(kk)_{0}$ ⁠	⁠ $d(kk)_{0}d$ ⁠	Иногда его называют Дж . ^[4] См. ниже объяснение обозначений соединения. Несоединяемая форма kk не является неприводимой.
10	${\begin{bma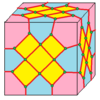trix}1&3&1\\0&10&0\\0&6&0\end{bmatrix}}$	Крест : Х	Хд	дХ	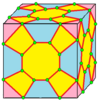dXd

Индексированные расширенные операции

Ряд операторов можно сгруппировать по некоторым критериям или изменить их поведение с помощью индекса. ^[4] Они записываются как оператор с индексом: x _n .

Увеличение

Операции увеличения сохраняют исходные края. Их можно применить к любому независимому подмножеству граней или преобразовать в форму соединения путем удаления исходных ребер. Нотация Конвея поддерживает дополнительный индекс для этих операторов: 0 для формы соединения или 3 или выше для количества сторон, которые имеют затронутые грани. Например, k ₄ Y ₄ =O: если взять пирамиду с квадратным основанием и приклеить к квадратному основанию еще одну пирамиду, получится октаэдр.

Оператор	к	л	л	К	(кк)
х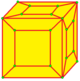
х ₀	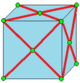к ₀ = j	л ₀ = с	Л ₀	К ₀ = jk	⁠ $(kk)_{0}$ ⁠
Увеличение	Пирамида	Призма	Антипризма

Оператор усечения t также имеет индексную форму t _n , указывающую, что усекаются только вершины определенной степени. эквивалентно dk _nd Это .

Некоторые расширенные операторы могут быть созданы в особых случаях с помощью операторов k _n и t _n . Например, куб со скошенной фаской , cC , может быть построен как t ₄ daC , как ромбический додекаэдр , daC или jC , с усеченными вершинами степени 4. Лофт-куб lC — это то же самое, что t ₄ kC . Квинто-додекаэдр, qD, может быть построен как t ₅ daaD или t ₅ deD или t ₅ oD , дельтоидный шестиконтаэдр , deD или oD , с усеченными вершинами степени 5.

Мета/Безель

Meta добавляет вершины в центре и по краям, а Bevel добавляет грани в центре, исходные вершины и вдоль краев. Индекс — это количество вершин или граней, добавленных по ребрам. Мета (в неиндексированной форме) также называется кантитрункацией или омнитрункацией . Обратите внимание, что 0 здесь не означает то же самое, что и для операций увеличения: это означает, что по ребрам добавляется ноль вершин (или граней). ^[4]

Мета/операторы скоса
н	Краевой фактор	Матрица $\mathbf {M} _{x}$	х	хд	дх	dxd
0	3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$	к = м ₀	н	г = б ₀	т
1	6	${\begin{bmatrix}1&1&1\\0&6&0\\0&4&0\end{bmatrix}}$	м = м ₁ = кдж		б = б ₁ = из
2	9	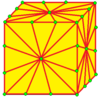${\begin{bmatrix}1&2&1\\0&9&0\\0&6&0\end{bmatrix}}$	m_м2	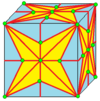м ₂ д	б ₂	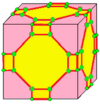б ₂ д
3	12	${\begin{bmatrix}1&3&1\\0&12&0\\0&8&0\end{bmatrix}}$	m ₃	m₃м3д	б ₃	б ₃ д
н	3 н +3	${\begin{bmatrix}1&n&1\\0&3n+3&0\\0&2n+2&0\end{bmatrix}}$	м _н	м _н д	б _н	б _н д

Медиальный

Медиальный похож на мета, за исключением того, что он не добавляет ребра из центра к каждой исходной вершине. Форма индекса 1 идентична орто-операторам Конвея и операторам расширения: расширение также называется кантелляцией и расширением . Обратите внимание, что o и e имеют свои собственные индексированные формы, описанные ниже. Также обратите внимание, что некоторые реализации начинают индексацию с 0 вместо 1. ^[4]

Медиальные операторы
н	Край фактор	Матрица $\mathbf {M} _{x}$	х	хд	дх	dxd
1	4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$	М ₁ = о = jj		е = аа
2	7	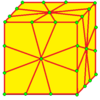${\begin{bmatrix}1&2&1\\0&7&0\\0&4&0\end{bmatrix}}$	Медиальный : М = М ₂	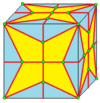Мэриленд	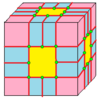дМ	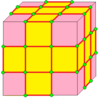ДМД
н	3н 1 +	${\begin{bmatrix}1&n&1\\0&3n+1&0\\0&2n&0\end{bmatrix}}$	М _н	М _н д	дМ _н	дМ _н д

Гольдберг-Коксетер

Операторы Гольдберга-Коксетера (GC) Конвея — это два бесконечных семейства операторов, которые являются расширением конструкции Гольдберга-Коксетера . ^[16]^[17] Построение GC можно рассматривать как взятие треугольного сечения треугольной решетки или квадратного сечения квадратной решетки и наложение его на каждую грань многогранника. Эту конструкцию можно распространить на любую грань, определив камеры треугольника или квадрата («главный многоугольник»). ^[7] Операторы треугольного семейства можно использовать для создания многогранников Гольдберга и геодезических многогранников : см . в Списке геодезических многогранников и многогранников Гольдберга формулы .

Этими двумя семействами являются треугольное семейство GC, ca _a,b и u _a,b , и четырехугольное семейство GC, e _a,b и o _a,b . Оба семейства GC индексируются двумя целыми числами. $a\geq 1$ и $b\geq 0$ . Они обладают многими приятными качествами:

Индексы семейств связаны с определенными евклидовыми областями над комплексными числами: целыми числами Эйзенштейна для треугольного семейства GC и целыми числами Гаусса для четырехугольного семейства GC.
Операторы в столбцах x и dxd внутри одного семейства коммутируют друг с другом.

Операторы разделены на три класса (примеры написаны на языке c , но применимы ко всем 4 операторам):

Класс I: ⁠ $b=0$ ⁠ . Ахиральный, сохраняет исходные края. Может быть записано с подавленным нулевым индексом, например c _{a ,0} = c _a .
Класс II: ⁠ $a=b$ ⁠ . Также ахиральный. Может быть разложено как c _a,a = c _a c _1,1
Класс III: Все остальные операторы. Они хиральны, а c _a,b и c _b,a являются киральными парами друг друга.

Из исходных операций Конвея единственные, которые не попадают в семейство GC, — это g и s (гироскоп и курносый). Мета и фаска ( m и b ) могут быть выражены через один оператор из треугольного семейства и один из четырехугольного семейства.

Треугольный

Треугольные операторы Гольдберга-Коксетера
а	б	Сорт	Краевой фактор Т = а ² + аб + б ²	Матрица $\mathbf {M} _{x}$	Мастер-треугольник	х	хд	дх	dxd
1	0	я	1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$		ты ₁ = С	д		с ₁ = С
2	0	я	4	${\begin{bmatrix}1&1&0\\0&4&0\\0&2&1\end{bmatrix}}$		ты ₂ = ты	округ Колумбия	из	с ₂ = с
3	0	я	9	${\begin{bmatrix}1&2&1\\0&9&0\\0&6&0\end{bmatrix}}$		ты ₃ = пп	такой как	зт	с ₃ = zz
4	0	я	16	${\begin{bmatrix}1&5&0\\0&16&0\\0&10&1\end{bmatrix}}$		ты ₄ = ты	ууд = DCC	дуэт = ccd	с ₄ = cc
5	0	я	25	${\begin{bmatrix}1&8&0\\0&25&0\\0&16&1\end{bmatrix}}$		ты ₅	ты ₅ d = постоянный ток ₅	ду ₅ = с ₅ д	с ₅
6	0	я	36	${\begin{bmatrix}1&11&1\\0&36&0\\0&24&0\end{bmatrix}}$		ты ₆ = отлично	чувак	Чт	ты ₆ = чзз
7	0	я	49	${\begin{bmatrix}1&16&0\\0&49&0\\0&32&1\end{bmatrix}}$		ты ₇ = ты _2,1 ты _1,2 = веревка	врвд = башня	дврв = врвд	c ₇ = c _2,1 c _1,2 = wrw
8	0	я	64	${\begin{bmatrix}1&21&0\\0&64&0\\0&42&1\end{bmatrix}}$		в ₈ = в ³	в ³д = постоянный ток ³	из ³ = с ³д	с ₈ = с ³
9	0	я	81	${\begin{bmatrix}1&26&1\\0&81&0\\0&54&0\end{bmatrix}}$		ты ₉ = п ⁴	н ³к = кз ³	ТН ³ = г ³т	с ₉ = z ⁴
1	1	II	3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$		ты _1,1 = п	к	т	в _1.1 = z
2	1	III	7	${\begin{bmatrix}1&2&0\\0&7&0\\0&4&1\end{bmatrix}}$		v = u _2,1	v = dw	дв = вд	ш = с _2.1
3	1	III	13	${\begin{bmatrix}1&4&0\\0&13&0\\0&8&1\end{bmatrix}}$		тебе _3,1	и _3,1 d = постоянный ток _3,1	ду _3,1 = с _3,1 д	в _3.1
3	2	III	19	${\begin{bmatrix}1&6&0\\0&19&0\\0&12&1\end{bmatrix}}$		тебе _3,2	и _3,2 d = постоянный ток _3,2	ду _3,2 = с _3,2 д	в _3.2
4	3	III	37	${\begin{bmatrix}1&12&0\\0&37&0\\0&24&1\end{bmatrix}}$		тебе _4,3	и _4,3 d = постоянный ток _4,3	ду _4,3 = с _4,3 д	в _4.3
5	4	III	61	${\begin{bmatrix}1&20&0\\0&61&0\\0&40&1\end{bmatrix}}$		тебе _5,4	u _5,4 d = постоянный ток _5,4	ду _5,4 = с _5,4 д	в _5.4
6	5	III	91	${\begin{bmatrix}1&30&0\\0&91&0\\0&60&1\end{bmatrix}}$		в _6,5 = в _1,2 в _1,3	u _6,5 d = постоянный ток _6,5	ду _6,5 = с _6,5 д	с _6,5 = с _1,2 с _1,3
7	6	III	127	${\begin{bmatrix}1&42&0\\0&127&0\\0&84&1\end{bmatrix}}$		и _7,6	u _7,6 d = постоянный ток _7,6	ду _7,6 = с _7,6 д	в _7.6
8	7	III	169	${\begin{bmatrix}1&56&0\\0&169&0\\0&112&1\end{bmatrix}}$		ты _8,7 = ты _3,1²	u _8,7 d = постоянный ток _8,7	ду _8,7 = с _8,7 д	с _8,7 = с _3,1²
9	8	III	217	${\begin{bmatrix}1&72&0\\0&217&0\\0&144&1\end{bmatrix}}$		ты _9,8 = ты _2,1 ты _5,1	u _9,8 d = постоянный ток _9,8	ду _9,8 = с _9,8 д	с _9,8 = с _2,1 с _5,1
$a\equiv b$ $\ (\mathrm {mod} \ 3)$		I, II или III	$T\equiv 0\$ $(\mathrm {mod} \ 3)$	${\begin{bmatrix}1&{\frac {T}{3}}-1&1\\0&T&0\\0&{\frac {2}{3}}T&0\end{bmatrix}}$	...	и _{а, б}	u _a,b d = dc _a,b	два _a,b = c _a,b d	такси
$a\not \equiv b$ $\ (\mathrm {mod} \ 3)$		я или III	$T\equiv 1$ $\ (\mathrm {mod} \ 3)$	${\begin{bmatrix}1&{\frac {T-1}{3}}&0\\0&T&0\\0&2{\frac {T-1}{3}}&1\end{bmatrix}}$	...	и _{а, б}	u _a,b d = dc _a,b	два _a,b = c _a,b d	такси

Согласно базовой теории чисел, для любых значений a и b , $T\not \equiv 2\ (\mathrm {mod} \ 3)$ .

Четырехугольник

Четырехсторонние операторы Гольдберга-Коксетера
а	б	Сорт	Краевой фактор Т = а ² + б ²	Матрица $\mathbf {M} _{x}$	Мастер-сквер	х	хд	дх	dxd
1	0	я	1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$		о ₁ = С	е ₁ = d		о ₁ = дд = S
2	0	я	4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$		о ₂ = о = j ²		е ₂ = е = а ²
3	0	я	9	${\begin{bmatrix}1&4&0\\0&9&0\\0&4&1\end{bmatrix}}$		о ₃	3		о ₃
4	0	я	16	${\begin{bmatrix}1&7&1\\0&16&0\\0&8&0\end{bmatrix}}$		о ₄ = о = j ⁴		е ₄ = ее = а ⁴
5	0	я	25	${\begin{bmatrix}1&12&0\\0&25&0\\0&12&1\end{bmatrix}}$		о ₅ = о _2,1 о _1,2 = прп	е ₅ = е _2,1 е _1,2		о ₅ = дпрпд
6	0	я	36	${\begin{bmatrix}1&17&1\\0&36&0\\0&18&0\end{bmatrix}}$		о ₆ = о ₂ о ₃		е ₆ = е ₂ е ₃
7	0	я	49	${\begin{bmatrix}1&24&0\\0&49&0\\0&24&1\end{bmatrix}}$		о ₇	e ₇		о ₇
8	0	я	64	${\begin{bmatrix}1&31&1\\0&64&0\\0&32&0\end{bmatrix}}$		о ₈ = о ³ = j ⁶		е ₈ = е ³ = а ⁶
9	0	я	81	${\begin{bmatrix}1&40&0\\0&81&0\\0&40&1\end{bmatrix}}$		о ₉ = о ₃²	е9 = e_е3²		о ₉
10	0	я	100	${\begin{bmatrix}1&49&1\\0&100&0\\0&50&0\end{bmatrix}}$		о ₁₀ = оо _2,1 о _1,2		е ₁₀ = ee _2,1 е _1,2
1	1	II	2	${\begin{bmatrix}1&0&1\\0&2&0\\0&1&0\end{bmatrix}}$		о _1,1 = j		е _1,1 = а
2	2	II	8	${\begin{bmatrix}1&3&1\\0&8&0\\0&4&0\end{bmatrix}}$		о _2,2 = j ³		е _2,2 = а ³
1	2	III	5	${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$		о _1,2 = р	е _1,2 = dp = pd		п
$a\equiv b$ $\ (\mathrm {mod} \ 2)$		I, II или III	Т даже	${\begin{bmatrix}1&{\frac {T}{2}}-1&1\\0&T&0\\0&{\frac {T}{2}}&0\end{bmatrix}}$	...	о _{а, б}		Да, _{а, б}
$a\not \equiv b$ $\ (\mathrm {mod} \ 2)$		я или III	Т нечетное	${\begin{bmatrix}1&{\frac {T-1}{2}}&0\\0&T&0\\0&{\frac {T-1}{2}}&1\end{bmatrix}}$	...	о _{а, б}	Да, _{а, б}		о _{а, б}

Примеры

Архимедовы и каталонские тела

Оригинальный набор операторов Конвея может создавать все архимедовы тела и каталанские тела , используя в качестве начальных тел Платоновы тела . (Обратите внимание, что оператор r не требуется для создания обеих киральных форм.)

Составные операторы

tI Усеченный икосаэдр можно , использовать в качестве затравки для создания некоторых более привлекательных многогранников, хотя они не являются ни вершинами ни транзитивными по граням .