Тороидальный многогранник

В геометрии — тороидальный многогранник это многогранник , который также является тороидом ( с g -дырками тор ), имеющий топологический род ( g ) 1 или больше. Яркие примеры включают многогранники Часара и Силасси .
Изменения в определении
[ редактировать ]Тороидальные многогранники определяются как совокупность многоугольников , которые пересекаются по своим краям и вершинам, образуя многообразие при этом . То есть каждое ребро должно быть общим ровно для двух многоугольников, и в каждой вершине ребра и грани, которые встречаются в вершине, должны быть связаны вместе в едином цикле чередования ребер и граней, связи вершины. Для тороидальных многогранников это многообразие является ориентируемой поверхностью . [1] Некоторые авторы ограничивают фразу «тороидальные многогранники», чтобы обозначить более конкретно многогранники, топологически эквивалентные тору (рода 1 ) . [2]
В этой области важно отличать вложенные тороидальные многогранники, грани которых представляют собой плоские многоугольники в трехмерном евклидовом пространстве , не пересекающие себя или друг друга, от абстрактных многогранников , топологических поверхностей без какой-либо заданной геометрической реализации. [3] Промежуточными между этими двумя крайностями являются многогранники, образованные геометрическими многоугольниками или звездчатыми многоугольниками в евклидовом пространстве, которым разрешено пересекать друг друга.
Во всех этих случаях тороидальность многогранника можно проверить по его ориентируемости и Эйлеровой характеристики неположительности . Эйлерова характеристика обобщается до V − E + F = 2 − 2 g , где g — ее топологический род.
Многогранники Часара и Силасси
[ редактировать ] | 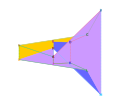 |
Двумя простейшими возможными вложенными тороидальными многогранниками являются многогранники Часара и Силасси.
Многогранник Часара представляет собой тороидальный многогранник с семью вершинами, 21 ребром и 14 треугольными гранями. [6] Он и тетраэдр — единственные известные многогранники, в которых каждый возможный отрезок, соединяющий две вершины, образует ребро многогранника. [7] Его двойственный многогранник Силасси имеет семь шестиугольных граней, примыкающих друг к другу. [8] тем самым обеспечивая существование половины теоремы о том, что максимальное количество цветов, необходимое для отображения на торе (первого рода), равно семи. [9]
Многогранник Часара имеет наименьшее количество возможных вершин среди всех вложенных тороидальных многогранников, а многогранник Силасси имеет наименьшее количество возможных граней среди всех вложенных тороидальных многогранников.
Тороидальный дельтаэдр Конвея
[ редактировать ]
Тороидальный дельтаэдр был описан Джоном Х. Конвеем в 1997 году и содержит 18 вершин и 36 граней. Некоторые смежные грани компланарны . Конвей предположил, что это должен быть дельтаэдрический тороид с наименьшим количеством возможных граней. [10]
Тороиды Стюарта
[ редактировать ]Особая категория тороидальных многогранников строится исключительно из правильных многоугольных граней без пересечений и с дополнительным ограничением, согласно которому соседние грани не могут лежать в одной плоскости друг с другом. Их называют тороидами Стюарта . [11] названы в честь Бонни Стюарт , которая их интенсивно изучала. [12] Они аналогичны телам Джонсона в случае выпуклых многогранников ; однако, в отличие от тел Джонсона, тороидов Стюарта бесконечно много. [13] К ним относятся также тороидальные дельтаэдры , многогранники, все грани которых представляют собой равносторонние треугольники.
Ограниченный класс тороидов Стюарта, также определенный Стюартом, представляет собой квазивыпуклые тороидальные многогранники . Это тороиды Стюарта, которые включают все края своей выпуклой оболочки . Для такого многогранника каждая грань выпуклой оболочки либо лежит на поверхности тороида, либо представляет собой многоугольник, все ребра которого лежат на поверхности тороида. [14]
| Род | 1 | 1 |
|---|---|---|
| Изображение | 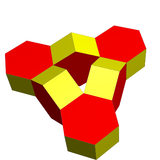 | 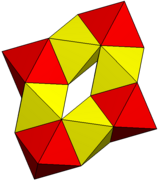 |
| Многогранники | 6 шестиугольных призм | 8 октаэдров |
| Вершины | 48 | 24 |
| Края | 84 | 72 |
| Лица | 36 | 48 |
| Род | 1 | 3 | 11 | 3 | 5 | 7 | 11 | |
|---|---|---|---|---|---|---|---|---|
| Изображение |  |  |  |  |  |  |  | 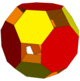 |
| Многогранники | 4 квадратных купола 8 тетраэдров | 6 треугольных куполов 6 квадратных пирамид | 4 треугольных купола 6 квадратных пирамид | 24 треугольные призмы 6 квадратных пирамид 8 тетраэдров | 6 квадратных куполов 4 треугольных купола 12 кубиков | 8 треугольных куполов 12 кубиков | 6 квадратных куполов 12 кубиков | 6 квадратных куполов 8 треугольных куполов |
| Выпуклая оболочка | усеченный куб | усеченный октаэдр | усеченный октаэдр | расширенный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр |
| Вершины | 32 | 30 | 30 | 62 | 72 | 72 | 72 | 72 |
| Края | 64 | 60 | 72 | 168 | 144 | 168 | 168 | 168 |
| Лица | 32 | 30 | 38 | 86 | 68 | 88 | 84 | 76 |
Самопересекающиеся многогранники
[ редактировать ] Октагемиоктаэдр |  Малый кубический октаэдр |  Большой додекаэдр |
Многогранник, образованный системой пересекающихся многоугольников, соответствует абстрактному топологическому многообразию, образованному его многоугольниками и их системой общих ребер и вершин, и род многогранника может быть определен на основе этого абстрактного многообразия. рода 1 Примеры включают октагемиоктаэдр рода 3 , малый кубубооктаэдр рода 4 и большой додекаэдр .
Корончатые многогранники
[ редактировать ]
Коронной многогранник или стефаноид — это тороидальный многогранник, который также является благородным , будучи одновременно изогональным (равные вершины) и изоэдральным (равные грани). Корончатые многогранники самопересекающиеся и топологически самодвойственные . [15]
См. также
[ редактировать ]- Проективный многогранник
- Косой апейроэдр (бесконечный косой многогранник)
- Сферический многогранник
- Тороидальный граф
Ссылки
[ редактировать ]- ^ Уайтли (1979) ; Стюарт (1980) , с. 15.
- ^ Уэббер, Уильям Т. (1997), «Моноэдральные идевалентные многогранники, являющиеся тороидами», Geometriae Dedicata , 67 (1): 31–44, doi : 10.1023/A:1004997029852 , MR 1468859 , S2CID 117884274 .
- ^ Уайтли, Уолтер (1979), «Реализуемость многогранников» (PDF) , Структурная топология (1): 46–58, 73, MR 0621628 .
- ^ Часар Акош, Многогранник без диагоналей. , Институт Боляи, Сегедский университет, 1949 г.
- ^ Грюнбаум, Бранко ; Силасси, Лайош (2009), «Геометрические реализации специальных тороидальных комплексов», Вклад в дискретную математику , 4 (1): 21–39, doi : 10.11575/cdm.v4i1.61986 , ISSN 1715-0868
- ^ Часар, А. (1949), «Многогранник без диагоналей», Acta Sci. Сегед , 13 : 140–142 .
- ^ Циглер, Гюнтер М. (2008), «Многогранные поверхности высокого рода», в Бобенко, А.И.; Шредер, П.; Салливан, Дж. М .; Циглер, Г.М. (ред.), Дискретная дифференциальная геометрия , Семинары в Обервольфахе, том. 38, Springer-Verlag, стр. 191–213, arXiv : math.MG/0412093 , doi : 10.1007/978-3-7643-8621-4_10 , ISBN 978-3-7643-8620-7 , S2CID 15911143 .
- ^ Силасси, Лайош (1986), «Регулярные тороиды», Структурная топология , 13 : 69–80, hdl : 2099/1038 .
- ^ Хивуд, П.Дж. (1890), «Теоремы о раскраске карт», Ежеквартальный журнал математики , первая серия, 24 : 322–339
- ^ Конвей, Джон, «Многогранники положительного рода» , Geometry.research Usenet группа ; см. сообщения от «23 сентября 1997 г., 00:00:00», анонсирующие тороидальный дельтаэдр, и «25 сентября 1997 г., 00:00:00», описывающие его конструкцию. В отличие от тороидов § Стюарта , он имеет копланарные смежные треугольники, но в остальном напоминает тороидальный дельтаэдр с большим количеством граней, описанный Стюартом (1980) , с. 60.
- ^ Уэбб, Роберт (2000), «Стелла: навигатор многогранника» , Симметрия: культура и наука , 11 (1–4): 231–268, MR 2001419 .
- ^ Стюарт, Б.М. (1980), Приключения среди тороидов: исследование ориентируемых многогранников с правильными гранями (2-е изд.), Б.М. Стюарт, ISBN 978-0-686-11936-4 .
- ^ Стюарт (1980) , с. 15.
- ^ Стюарт (1980) , «Квазивыпуклость и слабая квазивыпуклость», стр. 76–79.
- ^ Грюнбаум, Бранко (1994), «Многогранники с полыми гранями» , Многогранники: абстрактные, выпуклые и вычислительные , НАТО ASI, серия C: Математическая и физическая серия, том. 440, Kluwer Academic Publishers, стр. 43–70, номер документа : 10.1007/978-94-011-0924-6_3 . См., в частности, стр. 60 .