Ссылка (симплициальный комплекс)

Ссылка в симплициальном комплексе является обобщением окрестности вершины графа. Ссылка вершины кодирует информацию о локальной структуре комплекса в вершине.

Ссылка вершины

Учитывая абстрактный симплициальный комплекс $X$ и ${\textstyle v}$ вершина в ${\textstyle V(X)}$ , его ссылка ${\textstyle \operatorname {Lk} (v,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такой, что ${\textstyle v\not \in \tau }$ и ${\textstyle \tau \cup \{v\}}$ лицом $X.$ является

В частном случае, когда $X$ является одномерным комплексом (то есть графом ), ${\textstyle \operatorname {Lk} (v,X)}$ содержит все вершины ${\textstyle u\neq v}$ такой, что ${\textstyle \{u,v\}}$ — ребро графа; то есть, ${\textstyle \operatorname {Lk} (v,X)={\mathcal {N}}(v)=}$ окрестности ${\textstyle v}$ в графике.

Учитывая геометрический симплициальный комплекс $X$ и ${\textstyle v\in V(X)}$ , его ссылка ${\textstyle \operatorname {Lk} (v,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такой, что ${\textstyle v\not \in \tau }$ и есть симплекс ${\textstyle X}$ у которого есть ${\textstyle v}$ как вершина и ${\textstyle \tau }$ как лицо. ^[1]^: 3 Эквивалентно, соединение ${\textstyle v\star \tau }$ это лицо в ${\textstyle X}$ . ^[2]^: 20

В качестве примера предположим, что v — верхняя вершина тетраэдра слева. Тогда звено v — это треугольник в основании тетраэдра. Это связано с тем, что для каждого ребра этого треугольника соединение v с ребром представляет собой треугольник (один из трех треугольников на сторонах тетраэдра); а соединение v с самим треугольником представляет собой весь тетраэдр.
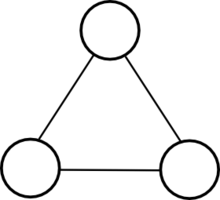
Звеном вершины тетраэдра является треугольник.

Альтернативное определение: ссылка вершины ${\textstyle v\in V(X)}$ — граф $Lk(v, X),$ построенный следующим образом. Вершины $Lk(v, X)$ — это ребра $X,$ инцидентные $v$ . Два таких ребра смежны в $Lk(v, X)$ тогда и только тогда, когда они инцидентны общей 2-клетке в точке $v$ .

Графу $Lk(v, X)$ часто задают топологию шара ; малого радиуса с центром в $v$ точке это аналог сферы с центром в точке. ^[3]

Ссылка на лицо

Определение связи может быть расширено от одной вершины до любой грани.

Дан абстрактный симплициальный комплекс $X$ и любая грань ${\textstyle \sigma }$ X $ссылка$ , его ${\textstyle \operatorname {Lk} (\sigma ,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такой, что ${\textstyle \sigma ,\tau }$ непересекающиеся и ${\textstyle \tau \cup \sigma }$ является лицом $X$ : ${\textstyle \operatorname {Lk} (\sigma ,X):=\{\tau \in X:~\tau \cap \sigma =\emptyset ,~\tau \cup \sigma \in X\}}$ .

Дан геометрический симплициальный комплекс $X$ и любая грань ${\textstyle \sigma \in X}$ , его ссылка ${\textstyle \operatorname {Lk} (\sigma ,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такой, что ${\textstyle \sigma ,\tau }$ не пересекаются и существует симплекс ${\textstyle X}$ у этого есть оба ${\textstyle \sigma }$ и ${\textstyle \tau }$ как лица. ^[1]^: 3

Примеры

Звено вершины тетраэдра представляет собой треугольник: три вершины звена соответствуют трем ребрам, инцидентным вершине, а три ребра звена соответствуют граням, инцидентным вершине. В этом примере связь можно визуализировать, отсекая вершину плоскостью; формально, пересекая тетраэдр плоскостью вблизи вершины – полученное сечение и есть звено.

Другой пример показан ниже. Существует двумерный симплициальный комплекс. Слева вершина отмечена желтым цветом. Справа ссылка на эту вершину отмечена зеленым цветом.

А вершина и ее связь .

Характеристики

Для любого симплициального комплекса $X$ каждое звено ${\textstyle \operatorname {Lk} (\sigma ,X)}$ закрыт сверху вниз и, следовательно, тоже является симплициальным комплексом; это подкомплекс $X$ .
Поскольку $X$ симплициально, существует изоморфизм множеств между ${\textstyle \operatorname {Lk} (\sigma ,X)}$ и набор $X_{\sigma }:=\{\rho \in X{\text{ such that }}\sigma \subseteq \rho \}$ : каждый ${\textstyle \tau \in \operatorname {Lk} (\sigma ,X)}$ соответствует ${\textstyle \tau \cup \sigma }$ , который находится в $X_{\sigma }$ .

Ссылка и звездочка

Понятие, тесно связанное со ссылкой, — это звезда .

Дан абстрактный симплициальный комплекс $X$ и любая грань ${\textstyle \sigma \in X}$ , ${\textstyle V(X)}$ , это звезда ${\textstyle \operatorname {St} (\sigma ,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такой, что ${\textstyle \tau \cup \sigma }$ лицом $X.$ является В частном случае, когда $X$ является одномерным комплексом (то есть графом ), ${\textstyle \operatorname {St} (v,X)}$ содержит все ребра ${\textstyle \{u,v\}}$ для всех вершин ${\textstyle u}$ которые являются соседями ${\textstyle v}$ . То есть это звезда теории графов с центром в ${\textstyle u}$ .

Дан геометрический симплициальный комплекс $X$ и любая грань ${\textstyle \sigma \in X}$ , это звезда ${\textstyle \operatorname {St} (\sigma ,X)}$ это набор, содержащий каждое лицо ${\textstyle \tau \in X}$ такая, что существует симплекс ${\textstyle X}$ имея оба ${\textstyle \sigma }$ и ${\textstyle \tau }$ как лица: ${\textstyle \operatorname {St} (\sigma ,X):=\{\tau \in X:\exists \rho \in X:\tau ,\sigma {\text{ are faces of }}\rho \}}$ . Другими словами, это замыкание множества ${\textstyle \{\rho \in X:\sigma {\text{ is a face of }}\rho \}}$ -- множество симплексов, имеющих ${\textstyle \sigma }$ как лицо.

Таким образом, ссылка является подмножеством звезды. Звездочка и ссылка связаны следующим образом:

Для любого ${\textstyle \sigma \in X}$ , ${\textstyle \operatorname {Lk} (\sigma ,X)=\{\tau \in \operatorname {St} (\sigma ,X):\tau \cap \sigma =\emptyset \}}$ . ^[1]^: 3
Для любого ${\textstyle v\in V(X)}$ , ${\textstyle \operatorname {St} (v,X)=v\star \operatorname {Lk} (v,X)}$ , то есть звезда ${\textstyle v}$ является конусом его звена в ${\textstyle v}$ . ^[2]^: 20

Пример проиллюстрирован ниже. Существует двумерный симплициальный комплекс. Слева вершина отмечена желтым цветом. Справа звезда этой вершины отмечена зеленым цветом.

А вершина и ее звезда .

См. также

Вершинная фигура — геометрическое понятие, подобное симплициальному звену.

Ссылки

^ Jump up to: ^а ^б ^с Брайант, Джон Л. (1 января 2001 г.), Даверман, Р.Дж.; Шер, Р.Б. (ред.), «Глава 5 — Кусочно-линейная топология» , Справочник по геометрической топологии , Амстердам: Северная Голландия, стр. 219–259, ISBN 978-0-444-82432-5 , получено 15 ноября 2022 г.
^ Jump up to: ^а ^б Рурк, Колин П .; Сандерсон, Брайан Дж. (1972). Введение в кусочно-линейную топологию . дои : 10.1007/978-3-642-81735-9 . ISBN 978-3-540-11102-3 .
^ Бридсон, Мартин ; Хефлигер, Андре (1999), Метрические пространства неположительной кривизны , Springer , ISBN 3-540-64324-9

[:0-1] Jump up to: ^а ^б ^с Брайант, Джон Л. (1 января 2001 г.), Даверман, Р.Дж.; Шер, Р.Б. (ред.), «Глава 5 — Кусочно-линейная топология» , Справочник по геометрической топологии , Амстердам: Северная Голландия, стр. 219–259, ISBN 978-0-444-82432-5 , получено 15 ноября 2022 г.

[:1-2] Jump up to: ^а ^б Рурк, Колин П .; Сандерсон, Брайан Дж. (1972). Введение в кусочно-линейную топологию . дои : 10.1007/978-3-642-81735-9 . ISBN 978-3-540-11102-3 .

[3] Бридсон, Мартин ; Хефлигер, Андре (1999), Метрические пространства неположительной кривизны , Springer , ISBN 3-540-64324-9

[1]

[2]

[3]