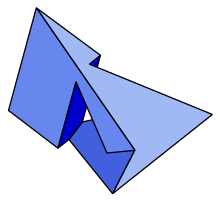
Многогранник Силасси
| Многогранник Силасси | |
|---|---|
 | |
| Тип | Тороидальный многогранник |
| Лица | 7 шестиугольников |
| Края | 21 |
| Вершины | 14 |
| Эйлер чар. | 0 (Род 1) |
| Конфигурация вершин | 6.6.6 |
| Группа симметрии | С 1 , [ ] + , (11) |
| Двойной многогранник | Императорский многогранник |
| Характеристики | Невыпуклый |
В геометрии — многогранник Силасси невыпуклый многогранник , топологически тор , с семью шестиугольными гранями.
Цвет и симметрия
[ редактировать ]14 вершин и 21 ребро многогранника Силасси образуют вложение графа Хивуда на поверхность тора. [1] Каждая грань этого многогранника имеет общее ребро с каждой другой гранью. В результате для окраски всех соседних граней требуется семь цветов. Этот пример показывает, что на поверхностях, топологически эквивалентных тору , для некоторых подразделений требуется семь цветов, что обеспечивает нижнюю оценку теоремы о семи цветах . Другая половина теоремы утверждает, что все тороидальные подразделения можно раскрасить семью или меньшим количеством цветов.
Многогранник Силасси имеет ось симметрии 180 градусов . Эта симметрия меняет местами три пары конгруэнтных граней, оставляя один непарный шестиугольник, имеющий ту же вращательную симметрию, что и многогранник.
Полное прилегание лица
[ редактировать ]Тетраэдр и многогранник Силасси — единственные два известных многогранника, в которых каждая грань имеет общее ребро с другой гранью.
Если многогранник с f гранями вложен в поверхность с h отверстиями таким образом, что каждая грань имеет общее ребро с каждой другой гранью, из этого следует путем некоторых манипуляций с эйлеровой характеристикой , что
Это уравнение выполняется для тетраэдра с h = 0 и f = 4 и для многогранника Силасси с h = 1 и f = 7.
Следующее возможное решение h = 6 и f = 12 будет соответствовать многограннику с 44 вершинами и 66 ребрами. Однако неизвестно, можно ли реализовать такой многогранник геометрически без самопересечений (а не как абстрактный многогранник ). В более общем смысле это уравнение может удовлетворяться именно тогда, когда f конгруэнтно 0, 3, 4 или 7 по модулю 12. [2] [3]
- Интерактивная орфографическая проекция, в которой каждое лицо имеет свой цвет. На изображении SVG перемещайте мышь влево и вправо, чтобы повернуть модель.
- Анимация
История
[ редактировать ]
Многогранник Силасси назван в честь венгерского математика Лайоша Силасси , открывшего его в 1977 году. [4] [1] Двойственный ( многограннику Силасси, многогранник Часара , был открыт ранее Акошом Часаром ; 1949 ) у него семь вершин, 21 ребро, соединяющее каждую пару вершин, и 14 треугольных граней. Как и многогранник Силасси, многогранник Часара имеет топологию тора. [5]
Ссылки
[ редактировать ]- ^ Jump up to: Перейти обратно: а б Силасси, Лайош (1986), «Регулярные тороиды» (PDF) , Структурная топология , 13 : 69–80
- ^ Юнгерман, М.; Рингель, Герхард (1980), «Минимальные триангуляции на ориентируемых поверхностях», Acta Mathematica , 145 (1–2): 121–154, doi : 10.1007/BF02414187
- ^ Грюнбаум, Бранко ; Силасси, Лайош (2009), «Геометрические реализации специальных тороидальных комплексов», Вклад в дискретную математику , 4 (1): 21–39, doi : 10.11575/cdm.v4i1.61986 , MR 2541986
- ^ Гарднер, Мартин (1978), «В котором математическая эстетика применяется к современному минималистическому искусству», Mathematical Games, Scientific American , 239 (5): 22–32, doi : 10.1038/scientificamerican1178-22 , JSTOR 24955839
- ^ Часар, Акос (1949), «Многогранник без диагоналей», Acta Sci. Сегед , 13 : 140–142.
Внешние ссылки
[ редактировать ]- Эйс, Том, Многогранник Силасси .
- Петерсон, Иварс (2007), «Многогранник с отверстием», MathTrek , Математическая ассоциация Америки .
- Вайсштейн, Эрик В. , «Многогранник Силасси» , MathWorld
- Многогранник Силасси — модель из бумаги на CutOutFoldUp.com


