График Хивуда
| График Хивуда | |
|---|---|
 | |
| Назван в честь | Перси Джон Хивуд |
| Вершины | 14 |
| Края | 21 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 6 |
| Автоморфизмы | 336 ( ПГЛ 2 (7) ) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Род | 1 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | двусторонний Кубический Клетка Дистанционно-транзитивный Дистанционно-регулярный Тороидальный гамильтониан Симметричный Ориентированно просто |
| Таблица графиков и параметров | |
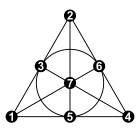
В математической области теории графов граф Хивуда — это неориентированный граф с 14 вершинами и 21 ребром, названный в честь Перси Джона Хивуда . [1]
Комбинаторные свойства
[ редактировать ]Граф является кубическим , и все циклы в графе имеют шесть или более ребер. Каждый меньший кубический граф имеет более короткие циклы, поэтому этот граф является 6- клеточным , наименьшим кубическим графом обхвата 6. Это дистанционно-транзитивный граф (см. перепись Фостера ) и, следовательно, дистанционно регулярный . [2]
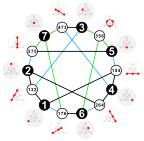
имеется 24 идеальных паросочетания В графе Хивуда ; для каждого паросочетания набор ребер, не входящих в паросочетание, образует гамильтонов цикл . Например, на рисунке показаны вершины графа, помещенные в цикл, причем внутренние диагонали цикла образуют паросочетание. Разделив ребра цикла на два паросочетания, мы можем разделить граф Хивуда на три идеальных паросочетания (то есть раскрасить его ребра в 3 цвета ) восемью различными способами. [2] Любые два совершенных паросочетания и любые два гамильтоновых цикла могут быть преобразованы друг в друга за счет симметрии графа. [3]
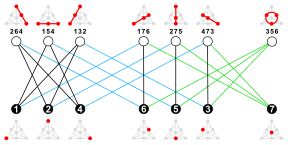
В графе Хивуда 28 шестивершинных циклов. Каждый 6-цикл не пересекается ровно с тремя другими 6-циклами; среди этих трех 6-циклов каждый представляет собой симметричную разность двух других. Граф с одним узлом на 6 циклов и одним ребром на каждую непересекающуюся пару 6 циклов является графом Кокстера . [4]
Геометрические и топологические свойства
[ редактировать ]
Граф Хивуда является тороидальным графом ; т. е. его можно вложить без пересечений на тор . Результатом является правильное отображение {6,3} 2,1 с 7 шестиугольными гранями. [5] Каждая грань карты примыкает к каждой другой грани, поэтому для раскраски карты требуется 7 цветов. Карта и график были обнаружены Перси Джоном Хивудом в 1890 году, который доказал, что ни одна карта тора не может требовать более семи цветов и, следовательно, эта карта является максимальной. [6] [7]
Эту карту можно точно представить как многогранник Силасси . [8] единственный известный многогранник, кроме тетраэдра , у которого каждая пара граней смежна.
Граф Хивуда — это граф Леви плоскости Фано , [5] график, представляющий инцидентность между точками и линиями в этой геометрии. При такой интерпретации 6-циклы в графе Хивуда соответствуют треугольникам в плоскости Фано. Кроме того, граф Хивуда является зданием Титса группы SL 3 (F 2 ) .
Граф Хивуда имеет номер пересечения 3 и является наименьшим кубическим графом с этим номером пересечения (последовательность A110507 в OEIS ). Включая граф Хивуда, существует 8 различных графов порядка 14 с номером пересечения 3.
Граф Хивуда — это наименьший кубический граф с инвариантом графа Колена де Вердьера μ = 6 . [9]
Граф Хивуда представляет собой граф с единичными расстояниями : его можно встроить в плоскость так, чтобы соседние вершины находились на расстоянии точно в единицу друг от друга, при этом не было двух вершин, вложенных в одну и ту же точку, и ни одной вершины, вложенной в точку внутри ребра. [10]
Алгебраические свойства
[ редактировать ]Группа автоморфизмов графа Хивуда изоморфна проективной линейной группе PGL 2 (7), группе порядка 336. [11] Он действует транзитивно на вершинах, ребрах и дугах графа. Следовательно, граф Хивуда является симметричным графом . Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Более строго, граф Хивуда является транзитивным по 4 дугам . [12] Согласно переписи Фостера , граф Хивуда, обозначенный как F014A, является единственным кубически-симметричным графом с 14 вершинами. [13] [14]
Имеет толщину книги 3 и номер очереди 2. [15]
Характеристический полином графа Хивуда равен . Это единственный граф с этим характеристическим полиномом, что делает его графом, определяемым его спектром.
Галерея
[ редактировать ]- переезд №3
- встроенный в тор ( показан квадратом )
- встроенный в тор (сравнить видео )
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «График Хивуда» . Математический мир .
- ^ Jump up to: Перейти обратно: а б Брауэр, Андриес Э. «График Хивуда» . Дополнения и исправления к книге «Дистанционно-регулярные графы» (Брауэр, Коэн, Ноймайер; Springer; 1989).
- ^ Абреу, М.; Олдред, REL; Функ, М.; Джексон, Билл; Лаббате, Д.; Шихан, Дж. (2004), «Графы и орграфы со всеми изоморфными 2-факторами», Журнал комбинаторной теории, серия B , 92 (2): 395–404, doi : 10.1016/j.jctb.2004.09.004 , MR 2099150 .
- ^ Дейтер, Итало Дж. (2011), «От графа Коксетера к графу Клейна», Journal of Graph Theory , 70 : 1–9, arXiv : 1002.1960 , doi : 10.1002/jgt.20597 , S2CID 754481 .
- ^ Jump up to: Перейти обратно: а б Коксетер (1950), «Самодуальные конфигурации и регулярные графы» (PDF) , Бюллетень Американского математического общества , 56 , doi : 10.1090/S0002-9904-1950-09407-5
- ^ Браун, Эзра (2002). «Множество имен (7,3,1)» (PDF) . Журнал «Математика» . 75 (2): 83–94. дои : 10.2307/3219140 . JSTOR 3219140 . Архивировано из оригинала (PDF) 5 февраля 2012 г. Проверено 27 октября 2006 г.
- ^ Хивуд, П.Дж. (1890). «Теорема о цвете карты». Ежеквартальный математический журнал . Первая серия. 24 : 322–339.
- ^ Силасси, Лайош (1986), «Регулярные тороиды» (PDF) , Структурная топология , 13 : 69–80
- ^ Хайн ван дер Холст (2006). «Графы и препятствия в четырех измерениях» (PDF) . Журнал комбинаторной теории, серия B. 96 (3): 388–404. дои : 10.1016/j.jctb.2005.09.004 .
- ^ Гербрахт, Эберхард Х.-А. (2009), Вложения графа Хивуда на одиннадцать единиц расстояния , arXiv : 0912.5395 , Bibcode : 2009arXiv0912.5395G .
- ^ Бонди, JA ; Мурти, USR (1976). Теория графов с приложениями . Нью-Йорк: Северная Голландия. п. 237 . ISBN 0-444-19451-7 . Архивировано из оригинала 13 апреля 2010 г. Проверено 18 декабря 2019 г.
- ^ Кондер, Марстон; Мортон, Маргарет (1995). «Классификация трехвалентных симметричных графов малого порядка» (PDF) . Австралазийский журнал комбинаторики . 11 : 146.
- ^ Ройл, Г. «Кубические симметричные графы (перепись Фостера)». Архивировано 20 июля 2008 г. в Wayback Machine.
- ^ Кондер М. и Добчани П. «Трехвалентные симметричные графы до 768 вершин». Дж. Комбин. Математика. Комбинировать. Вычислить. 40, 41–63, 2002.
- ^ Джессика Вольц, Разработка линейных макетов с помощью SAT . Магистерская диссертация, Тюбингенский университет, 2018 г.