Граф Кокстера
| Граф Кокстера | |
|---|---|
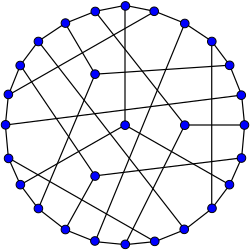 Граф Кокстера | |
| Назван в честь | HSM Коксетер |
| Вершины | 28 |
| Края | 42 |
| Радиус | 4 |
| Диаметр | 4 |
| Обхват | 7 |
| Автоморфизмы | 336 ( ПГЛ 2 (7)) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Симметричный Дистанционно-регулярный Дистанционно-транзитивный Кубический Гипогамильтониан |
| Таблица графиков и параметров | |
В математической области теории графов граф Кокстера представляет собой 3- регулярный граф с 28 вершинами и 42 ребрами. [1] Это один из 13 известных кубических дистанционно регулярных графов . [2] Он назван в честь Гарольда Скотта Макдональда Коксетера .
Свойства [ править ]
Граф Коксетера имеет хроматическое число 3, хроматический индекс 3, радиус 4, диаметр 4 и обхват 7. Это также 3 -связный граф и 3 -связный граф . Имеет толщину книги 3 и номер очереди 2. [3]
Граф Кокстера является гипогамильтоновым : сам по себе он не имеет гамильтонова цикла, но каждый граф, образованный удалением из него одной вершины, является гамильтоновым. Он имеет прямолинейный номер пересечения 11 и является наименьшим кубическим графом с таким номером пересечения. [4] (последовательность A110507 в OEIS ).
Строительство [ править ]
Простейшая конструкция графа Кокстера — из плоскости Фано . Возьмите 7 C 3 = 35 возможных 3-комбинаций по 7 предметам. Отбросьте 7 троек, соответствующих линиям плоскости Фано, оставив 28 троек. Соедините две тройки, если они не пересекаются. Результатом является график Кокстера. (См. изображение .) Эта конструкция представляет граф Коксетера как индуцированный подграф нечетного графа O 4 , также известного как граф Кнезера KG 7,3 .
Граф Коксетера также может быть построен из меньшего дистанционно регулярного графа Хивуда путем построения вершины для каждого 6-цикла в графе Хивуда и ребра для каждой непересекающейся пары 6-циклов. [5]
Граф Коксетера может быть получен из графа Хоффмана-Синглтона . Возьмем любую вершину v графа Хоффмана-Синглтона. Существует независимый набор размером 15, который включает v . Удалите 7 соседей v и весь независимый набор, включая v , оставив граф Коксетера.
Алгебраические свойства [ править ]
Группа автоморфизмов графа Кокстера — это группа порядка 336. [6] Он действует транзитивно на вершинах, ребрах и дугах графа. Следовательно, граф Кокстера является симметричным графом . Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно переписи Фостера , граф Коксетера, обозначаемый как F28A, является единственным кубически-симметричным графом с 28 вершинами. [7]
Граф Кокстера также однозначно определяется его спектром графа , набором собственных значений графа его матрицы смежности . [8]
Как конечный связный вершинно-транзитивный граф, не содержащий гамильтонова цикла , граф Кокстера является контрпримером к варианту гипотезы Ловаса , но каноническая формулировка гипотезы требует гамильтонова пути и проверяется графом Кокстера.
Известны только пять примеров вершинно-транзитивных графов без гамильтоновых циклов: полный граф K 2 , граф Петерсена , граф Коксетера и два графа, полученные из графов Петерсена и Кокстера путем замены каждой вершины треугольником. [9]
Характеристический полином графа Кокстера равен . Это единственный граф с этим характеристическим полиномом, что делает его графом, определяемым его спектром.
Галерея [ править ]
Макеты [ править ]
Это разные представления графа Коксетера, использующие одни и те же метки вершин. Есть четыре цвета и семь вершин каждого цвета.
Каждая красная, зеленая или синяя вершина соединена с двумя вершинами одного цвета (тонкие ребра, образующие 7-циклов) и с одной белой вершиной (толстые ребра).
красный семиугольник , зеленая тупая и синяя острая гептаграмма слева: 7-кратная вращательная симметрия |  3-кратная вращательная симметрия |  (сравните вариант с вершинами плоскости Фано ) |  зеркальная симметрия |
Свойства [ править ]
 |  |  |
Ссылки [ править ]
- ^ Вайсштейн, Эрик В. «График Кокстера» . Математический мир .
- ^ Брауэр, А.Э.; Коэн, AM; и Ноймайер А. Дистанционно-регулярные графы. Нью-Йорк: Springer-Verlag, 1989.
- ^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Хейторп, Майкл; Ньюкомб, Алекс (2018), Кубических графов на 26 вершинах с номером пересечения 11 не существует , arXiv : 1804.10336
- ^ Дейтер, Итало Дж. (2011), «От графа Коксетера к графу Клейна», Journal of Graph Theory , 70 : 1–9, arXiv : 1002.1960 , doi : 10.1002/jgt.20597 , S2CID 754481 .
- ^ Ройл, данные G. F028A.
- ^ Кондер М. и Добчани П. «Трехвалентные симметричные графы до 768 вершин». Дж. Комбин. Математика. Комбинировать. Вычислить. 40, 41–63, 2002.
- ^ ER van Dam и WH Haemers, Спектральные характеристики некоторых дистанционно-регулярных графов. Дж. Алгебраическая комбинация. 15, стр. 189-202, 2003 г.
- ^ Ройл, Г. «Кубические симметричные графы (перепись Фостера)». Архивировано 12 сентября 2015 г. в Wayback Machine.
- Коксетер, HSM «Мой график». Учеб. Лондонская математика. Соц. 46, 117–136, 1983.


