Гипогамильтониан граф

Не путать с гамильтоновым графиком .

Гипогамильтонов граф, построенный Линдгреном (1967) .

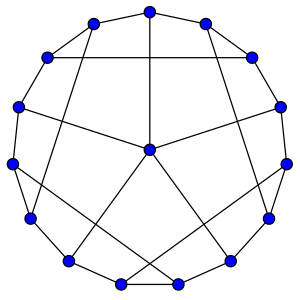
В математической области теории графов граф G называется гипогамильтоновым, если сам G не имеет гамильтонова цикла , но каждый граф, образованный удалением одной вершины из G, является гамильтоновым .

История

Гипогамильтоновы графы были впервые изучены Сусселье (1963) . Линдгрен (1967) цитирует Годена, Герца и Росси (1964) и Бусакера и Саати (1965) как дополнительные ранние статьи по этой теме; еще одна ранняя работа - Герц, Дюби и Виге (1967) .

Гретшель (1980) резюмирует большую часть исследований в этой области следующим предложением: «Статьи, посвященные этим графам... обычно демонстрируют новые классы гипогамильтоновых или гипопрослеживаемых графов, показывающие, что для определенных порядков n такие графы действительно существуют или что они обладают странными и неожиданными свойствами».

Приложения

Гипогамильтоновы графы возникают при целочисленном программировании при решении задачи коммивояжера : некоторые виды гипогамильтоновых графов определяют грани многогранника коммивояжера , форму, определяемую как выпуклую оболочку множества возможных решений задачи коммивояжера, и эти грани могут быть используется в методах секущей плоскости для решения задачи. Гретшель (1980) отмечает, что вычислительная сложность определения того, является ли граф гипогамильтоновым, хотя и неизвестна, вероятно, будет высокой, что затрудняет поиск граней этих типов, за исключением тех, которые определяются небольшими гипогамильтоновыми графами; к счастью, самые маленькие графы приводят к самым сильным неравенствам для этого приложения.

Концепции, тесно связанные с гипогамильтонностью, также использовались Парком, Лимом и Кимом (2007) для измерения отказоустойчивости сетевых топологий для параллельных вычислений .

Характеристики

Каждый гипогамильтонов граф должен быть 3 -связным , поскольку удаление любых двух вершин оставляет гамильтонов путь, который является связным. Существуют n -вершинные гипогамильтоновы графы, в которых максимальная степень равна n /2 и в которых имеется примерно n ² /4 ребра.

Гипогамильтоновый график Томассена (1974b) с обхватом 3.

Герц, Дюби и Виге (1967) предположили, что каждый гипогамильтонов граф имеет обхват 5 или более, но это было опровергнуто Томассеном (1974b) , который нашел примеры с обхватом 3 и 4. Некоторое время было неизвестно, может ли гипогамильтонов граф быть планарный , но сейчас известно несколько примеров, наименьший из которых имеет 40 вершин. Каждый планарный гипогамильтонов граф имеет хотя бы одну вершину, имеющую только три инцидентных ребра.

Если 3-регулярный граф является гамильтоновым, его ребра можно раскрасить тремя цветами: использовать чередующиеся цвета для ребер гамильтонова цикла (который должен иметь четную длину по лемме о согласовании ) и третий цвет для всех остальных ребер. Следовательно, все снарки , кубические графы без мостов, требующие четырех цветов ребер, должны быть негамильтоновыми, а многие известные снарки являются гипогамильтоновыми. Каждый гипогамильтонов снарк бикритичен : удаление любых двух вершин оставляет подграф, ребра которого можно раскрасить только тремя цветами. Трехраскраску этого подграфа можно описать просто: после удаления одной вершины оставшиеся вершины содержат гамильтонов цикл. После удаления второй вершины этот цикл становится путем, края которого можно раскрасить, чередуя два цвета. Остальные ребра образуют совпадение и могут быть окрашены в третий цвет.

Цветовые классы любой 3-раскраски ребер 3-регулярного графа образуют три паросочетания, каждое из которых принадлежит ровно одному из паросочетаний.Гипогамильтоновы снарки не имеют разделения на паросочетания этого типа, но Хэггквист (2007) предполагает, что ребра любого гипогамильтоновых снарков могут использоваться для формирования шести паросочетаний, причем каждое ребро принадлежит ровно двум паросочетаниям. Это частный случай гипотезы Берджа–Фалкерсона о том, что любой снарк имеет шесть паросочетаний с этим свойством.

Гипогамильтоновы графы не могут быть двудольными: в двудольном графе вершину можно удалить, чтобы сформировать гамильтонов подграф, только если она принадлежит большему из двух цветовых классов графа. Однако каждый двудольный граф является индуцированным подграфом некоторого гипогамильтонового графа.

Примеры

Самый маленький гипогамильтонов граф — это граф Петерсена ( Herz, Duby & Vigué, 1967 ). В более общем смысле, обобщенный граф Петерсена GP( n ,2) является гипогамильтоновым, когда n равно 5 (mod 6); граф Петерсена является примером этой конструкции с n = 5.

Линдгрен (1967) нашел еще один бесконечный класс гипогамильтоновых графов, в которых число вершин равно 4 (по модулю 6). Конструкция Линдгрена состоит из цикла длины 3 (по модулю 6) и единственной центральной вершины; центральная вершина соединена с каждой третьей вершиной цикла ребрами, которые он называет спицами, а вершины, находящиеся на расстоянии двух позиций от каждой конечной точки спицы, соединены друг с другом. Опять же, наименьшим примером конструкции Линдгрена является граф Петерсена.

Дополнительные бесконечные семейства приведены Бонди (1972) , Дойеном и ван Диестом (1975) и Гуттом (1977) .

Перечисление

В 1973 году Вацлав Хватал доказал, что для всех достаточно больших n существует гипогамильтонов граф с n вершинами. Учитывая последующие открытия, Теперь известно, что «достаточно большой» означает, что такие графы существуют для всех n ≥ 18. Известен полный список гипогамильтоновых графов с не более чем 17 вершинами: это граф Петерсена с 10 вершинами, граф с 13 вершинами и граф с 15 вершинами, найденные в результате компьютерного поиска Герца (1968) , и четыре графа с 16 вершинами. Существует не менее тринадцати 18-вершинных гипогамильтоновых графов. Применяя метод триггера Хватала (1973) к графу Петерсена и цветочному снарку , можно показать, что количество гипогамильтоновых графов, а точнее количество гипогамильтоновых снарков, растет как экспоненциальная функция числа вершин.

Обобщения

Теоретики графов также изучали гипоотслеживаемые графы , графы, которые не содержат гамильтонов путь, но такие, что каждое подмножество из n - 1 вершин может быть соединено путем. Аналогичные определения гипогамильтонности и гипопрослеживаемости для ориентированных графов рассматривались рядом авторов.

Эквивалентное определение гипогамильтоновых графов состоит в том, что их самый длинный цикл имеет длину n - 1 и что пересечение всех самых длинных циклов пусто. Менке, Замфиреску и Замфиреску (1998) исследуют графы с тем же свойством, что пересечение самых длинных циклов пусто, но в которых длина самого длинного цикла короче n - 1. Герц (1968) определяет цикличность графа как наибольшее число k такой, что каждые k вершин принадлежат циклу; гипогамильтоновы графы - это именно те графы, которые имеют цикличность n - 1. Аналогично Парк, Лим и Ким (2007) определяют граф как гамильтонов с ƒ-неисправностью, если удаление не более ƒ вершин оставляет гамильтонов подграф. Шауэрте и Замфиреску (2006) изучают графы с цикличностью n - 2.

Ссылки

• Олдред, РА; Маккей, BD ; Вормальд, Северная Каролина (1997), «Малые гипогамильтоновы графы» (PDF) , J. Combinatorial Math. Комбинаторные вычисления. , 23 : 143–152 .
• Альспах, Б.Р. (1983), «Классификация гамильтоновых обобщенных графов Петерсена», Журнал комбинаторной теории , серия B, 34 (3): 293–312, doi : 10.1016/0095-8956(83)90042-4 , MR   0714452 .
• Бонди, Дж. А. (1972), «Вариации гамильтоновой темы», Canadian Mathematical Bulletin , 15 : 57–62, doi : 10.4153/CMB-1972-012-3 .
• Бусакер, Р.Г.; Саати, Т.Л. (1965), Конечные графы и сети , McGraw-Hill .
• Хватал, В. (1973), «Шлепанцы в гипогамильтоновых графах», Canadian Mathematical Bulletin , 16 : 33–41, doi : 10.4153/CMB-1973-008-9 , MR   0371722 .
• Хватал, В. ; Кларнер, Д.А.; Кнут, Д.Э. (1972), Избранные задачи комбинаторного исследования (PDF) , Tech. Отчет STAN-CS-72-292, факультет компьютерных наук, Стэнфордский университет .
• Коллиер, Дж. Б.; Шмейхель, EF (1977), «Новые триггерные конструкции для гипогамильтоновых графов», Discrete Mathematics , 18 (3): 265–271, doi : 10.1016/0012-365X(77)90130-3 , MR   0543828 .
• Дойен, Дж.; Ван Дист, В. (1975), «Новые семейства гипогамильтоновых графов», Discrete Mathematics , 13 (3): 225–236, doi : 10.1016/0012-365X(75)90020-5 , MR   0416979 .
• Фуке, Ж.-Л.; Жоливе, Ж.Л. (1978), «Гипогамильтоновы ориентированные графы», Cahiers Center Études Rech. Опера. , 20 (2): 171–181, МР   0498218 .
• Годен, Т.; Герц, П.; Росси (1964), «Решение задачи № 29», Ред. Франк. Поиск Оперативный , 8 : 214–218 .
• Гоеманс, Мишель X. (1995), «Сравнение действительных неравенств для TSP в наихудшем случае», Mathematical Programming , 69 (1–3): 335–349, CiteSeerX   10.1.1.52.8008 , doi : 10.1007/BF01585563 , S2CID   214113 .
• Гретшель, М. (1977), «Гипогамильтоновы грани симметричного многогранника коммивояжера», Journal of Applied Mathematics and Mechanics , 58 : 469–471 .
• Гретшель, М. (1980), «О монотонной симметричной задаче коммивояжера: гипогамильтоновы/гипоотслеживаемые графы и фасеты», Mathematics of Operations Research , 5 (2): 285–292, doi : 10.1287/moor.5.2.285 , JSTOR   3689157 .
• Гретшель, М .; Вакабаяши, Ю. (1980), «Гипогамильтоновы диграфы», Методы исследования операций , 36 : 99–119, Zbl   0436.05038 .
• Гретшель, М .; Вакабаяши, Ю. (1981), «О структуре монотонного асимметричного многогранника коммивояжера I: гипогамильтоновы грани», Discrete Mathematics , 24 : 43–59, doi : 10.1016/0012-365X(81)90021-2 .
• Гретшель, М .; Вакабаяши, Ю. (1984), «Конструкции гипоотслеживаемых орграфов», в Коттле, Р.В.; Келмансон, МЛ; Корте, Б. (ред.), Математическое программирование (Процедуры Международного конгресса, Рио-де-Жанейро, 1981) , Северная Голландия .
• Грюнбаум, Б. (1974), «Вершины, пропущенные самыми длинными путями или цепями», Журнал комбинаторной теории , серия A, 17 : 31–38, doi : 10.1016/0097-3165(74)90025-9 , MR   0349474 .
• Гутт, Симона (1977), «Бесконечные семейства гипогамильтоновых графов», Бельгийская королевская академия, Bulletin de la Classe des Sciences , 5e Série, 63 (5): 432–440, MR   0498243 .
• Хэггквист, Р. (2007), Мохар, Б .; Новаковски, Р.Дж.; Уэст, Д.Б. (ред.), «Проблема 443. Особый случай гипотезы Фулкерсона», Исследовательские задачи 5-й словенской конференции (Блед, 2003 г.), Discrete Mathematics , 307 (3–5): 650–658, doi : 10.1016 /j.disc.2006.07.013 .
• Хацель, В. (1979), «Плоский гипогамильтонов граф с 57 узлами», Math. , 243 (3): 213–216, doi : 10.1007/BF01424541 , MR   0548801 , S2CID   121794449 .
• Герц, Дж. К. (1968), «О цикличности графов», Компьютеры в математических исследованиях , Северная Голландия, стр. 97–107, МР   0245461 .
• Герц, JC; Дуби, Джей-Джей; Виге, Ф. (1967), «Систематический поиск гипогамильтоновых графов», в Розенстиле, П. (редактор), Теория графов: Международный симпозиум, Рим, 1966 , Париж: Гордон и Брич, стр. 153–159 .
• Джуянде, Мохаммадреза; Маккей, Брендан Д .; Остергорд, Патрик Р.Дж.; Петтерссон, Вилле Х.; Замфиреску, Кэрол Т. (2017), «Плоские гипогамильтоновы графы на 40 вершинах», Journal of Graph Theory , 84 (2): 121–133, arXiv : 1302.2698 , Bibcode : 2013arXiv1302.2698J , doi : 10.1002/jgt.220 15 .
• Капур, Сан-Франциско; Кронк, Х.В.; Лик, Д. Р. (1968), «Об обходах в графах», Canadian Mathematical Bulletin , 11 (2): 195–201, doi : 10.4153/CMB-1968-022-8 , MR   0229543 .
• Кронк, Х.В. (1969), Кли, В. (ред.), «Существует ли гипоотслеживаемый граф?», Research Issues, American Mathematical Monthly , 76 (7): 809–810, doi : 10.2307/2317879 , JSTOR   2317879 .
• Линдгрен, В. Ф. (1967), «Бесконечный класс гипогамильтоновых графов», American Mathematical Monthly , 74 (9): 1087–1089, doi : 10.2307/2313617 , JSTOR   2313617 , MR   0224501 .
• Мачайова, Э.; Шковиера, М. (2007), «Построение гипогамильтоновых снарков с циклической связностью 5 и 6» , Электронный журнал комбинаторики , 14 (1): R14, doi : 10.37236/936 .
• Менке, Б.; Замфиреску, ТИ; Замфиреску, CM (1998), «Пересечения самых длинных циклов в сеточных графах», Journal of Graph Theory , 25 (1): 37–52, doi : 10.1002/(SICI)1097-0118(199705)25:1<37: :AID-JGT2>3.0.CO;2-J .
• Моханти, СП; Рао, Д. (1981), «Семейство гипогамильтоновых обобщенных призм», Комбинаторика и теория графов , Конспект лекций по математике, том. 885, Springer-Verlag, стр. 331–338, doi : 10.1007/BFb0092278 , ISBN.  978-3-540-11151-1 .
• Парк, Ж.-Х.; Лим, Х.-С.; Ким, Х.-К. (2007), «Пансвязность и панцикличность гиперкубоподобных взаимосвязанных сетей с неисправными элементами», Theoretical Computer Science , 377 (1–3): 170–180, doi : 10.1016/j.tcs.2007.02.029 .
• Робертсон, Дж. Н. (1969), Графы, минимальные при ограничениях на обхват, валентность и связность , докторская диссертация, Ватерлоо, Онтарио: Университет Ватерлоо .
• Шауэрте, Борис; Замфиреску, Коннектикут (2006), «Регулярные графы, в которых каждая пара точек пропускается каким-то самым длинным циклом», An. унив. Крайова сер. Мат. Информ. , 33 : 154–173, HDL : 1854/LU-6901462 , MR   2359901 .
• Скупень, З. (1989), «Экспоненциально много гипогамильтоновых графов», Графы, гиперграфы и матроиды III (Proc. Conf. Kalsk, 1988) , Зелена-Гура: Высший инженерный колледж, стр. 123–132 . Цитируется Скупеньем (2007) .
• Скупень, З. (2007), «Экспоненциально много гипогамильтоновых снарков», 6-й Чешско-словацкий международный симпозиум по комбинаторике, теории графов, алгоритмам и приложениям , Электронные заметки по дискретной математике, том. 28, стр. 417–424, номер документа : 10.1016/j.endm.2007.01.059 .
• Сусселье, Р. (1963), Берж, К. (редактор), «Проблема № 29: Круг раздражительных», Приятные и восхитительные проблемы, Rev. Франк. Поиск Оперативный , 7 : 405–406 .
• Штеффен, Э. (1998), «Классификация и характеристики снарков», Discrete Mathematics , 188 (1–3): 183–203, doi : 10.1016/S0012-365X(97)00255-0 , MR   1630478 .
• Штеффен, Э. (2001), «О бикритических снарках», Math. Словакия , 51 (2): 141–150, MR   1841443 .
• Томассен, Карстен (1974a), «Гипогамильтоновы и гипопрослеживаемые графы», Discrete Mathematics , 9 : 91–96, doi : 10.1016/0012-365X(74)90074-0 , MR   0347682 .
• Томассен, Карстен (1974b), «О гипогамильтоновых графах», Discrete Mathematics , 10 (2): 383–390, doi : 10.1016/0012-365X(74)90128-9 , MR   0357226 .
• Томассен, Карстен (1976), «Плоские и бесконечные гипогамильтоновы и гипопрослеживаемые графы», Discrete Mathematics , 14 (4): 377–389, doi : 10.1016/0012-365X(76)90071-6 , MR   0422086 .
• Томассен, Карстен (1978), «Гипогамильтоновы графы и орграфы», Теория и приложения графов (Proc. Internat. Conf., Western Mich. Univ., Каламазу, Мичиган, 1976) , Конспекты лекций по математике, том. 642, Берлин: Springer-Verlag, стр. 557–571, ​​MR   0499523 .
• Томассен, Карстен (1981), «Плоские кубические гипогамильтоновы и гипопрослеживаемые графы», Журнал комбинаторной теории , серия B, 30 : 36–44, doi : 10.1016/0095-8956(81)90089-7 , MR   0609592 .
• Винер, Габор; Арайя, Макото (2009), Самый главный вопрос , arXiv : 0904.3012 , Бибкод : 2009arXiv0904.3012W .
• Замфиреску, Коннектикут; Замфиреску, Т.И. (2007), «Плоский гипогамильтонов граф с 48 вершинами», Journal of Graph Theory , 55 (4): 338–342, doi : 10.1002/jgt.20241 .

Внешние ссылки

• Вайсштейн, Эрик В. , «Гипогамильтонов график» , MathWorld