График единичного расстояния

Граф единичных расстояний с 16 вершинами и 40 ребрами.

В математике , особенно в геометрической теории графов , граф единичных расстояний — это граф, сформированный из набора точек евклидовой плоскости путем соединения двух точек, когда расстояние между ними равно единице. Чтобы отличить эти графы от более широкого определения, которое позволяет некоторым несмежным парам вершин находиться на расстоянии один, их также можно назвать графами строгих единичных расстояний или точными графами единичных расстояний . Как наследственное семейство графов , они могут быть охарактеризованы запрещенными индуцированными подграфами . К графам единичных расстояний относятся графы кактусов , графы спичек и пенни-графы , а также графы гиперкубов . Обобщенные графы Петерсена представляют собой нестрогие графы единичных расстояний.

Нерешенная проблема Пола Эрдеша спрашивает, сколько ребер имеет граф единичных расстояний на $n$ вершины могут иметь. Самая известная нижняя граница немного выше линейной по $n$– вдали от верхней границы , пропорциональной $n^{4/3}$. Количество цветов, необходимых для раскраски графов единичных расстояний, также неизвестно ( проблема Хадвигера-Нельсона ): для некоторых графов единичных расстояний требуется пять цветов, и каждый граф единичных расстояний можно раскрасить семью цветами. Для каждого алгебраического числа существует граф единичных расстояний с двумя вершинами, которые должны находиться на этом расстоянии друг от друга. Согласно теореме Бекмана-Куорлза , единственные плоские преобразования, сохраняющие все графы единичных расстояний, — это изометрии .

Можно эффективно построить граф единичных расстояний по его точкам. Нахождение всех единичных расстояний имеет применение в сопоставлении с образцом , где оно может стать первым шагом в поиске конгруэнтных копий более крупных образцов. Однако определение того, может ли данный граф быть представлен в виде графа единичных расстояний, является NP-трудным и, более конкретно, полным для экзистенциальной теории действительных чисел .

Определение

Граф Петерсена как граф единичных расстояний

Граф Мёбиуса – Кантора как подграф графа единичных расстояний

Граф единичных расстояний для набора точек на плоскости — это неориентированный граф, которого являются эти точки вершинами , с ребром между двумя вершинами, когда их евклидово расстояние равно единице. Абстрактный граф называется графом с единичными расстояниями, если можно найти различные местоположения на плоскости для его вершин, так что его ребра имеют единичную длину и все несмежные пары вершин имеют неединичные расстояния. Когда это возможно, абстрактный граф изоморфен графу единичных расстояний выбранных местоположений. Альтернативно, в некоторых источниках используется более широкое определение, позволяющее несмежным парам вершин находиться на единичном расстоянии. Полученные графы являются подграфами графов единичных расстояний (как определено здесь). Если терминология может быть неоднозначной, графы, в которых не-ребра должны находиться на расстоянии неединичного расстояния друг от друга, могут называться графами строгих единичных расстояний. или точные графики единичных расстояний . Подграфы графов единичных расстояний — это эквивалентные графы, которые можно нарисовать на плоскости, используя только одну длину ребра. Для краткости в этой статье они называются «нестрогими графами единичных расстояний».

Графики единичных расстояний не следует путать с графами единичных дисков , которые соединяют пары точек, когда их расстояние меньше или равно единице, и часто используются для моделирования сетей беспроводной связи.

Примеры

Полный граф на двух вершинах является графом единичных расстояний, как и полный граф на трех вершинах ( граф треугольника ), но не полный граф на четырех вершинах. Обобщая треугольный граф, каждый граф циклов представляет собой граф единичных расстояний, реализованный в виде правильного многоугольника . Два графа конечных единичных расстояний, соединенные в одной общей вершине, образуют еще один граф единичных расстояний, поскольку один можно вращать относительно другого, чтобы избежать нежелательных дополнительных единичных расстояний. Соединяя таким образом графы, каждое конечное дерево или граф кактуса можно реализовать как граф единичных расстояний.

гиперкуба Граф $Q_{4}$ имеет 16 вершин и 32 единичных расстояния

Граф Хэмминга $H(3,3)$ имеет 27 вершин и 81 единицу расстояния

Любое декартово произведение графов единичных расстояний дает другой граф единичных расстояний; однако то же самое нельзя сказать о некоторых других распространенных графовых продуктах. Например, сильное произведение графов , примененное к любым двум непустым графам, дает полные подграфы с четырьмя вершинами, которые не являются графами единичных расстояний. Декартовы произведения графов путей образуют сеточные графы любой размерности, декартовы произведения полного графа на двух вершинах представляют собой графы гиперкубов , а декартовы произведения треугольных графов являются графами Хэмминга. $H(d,3)$.

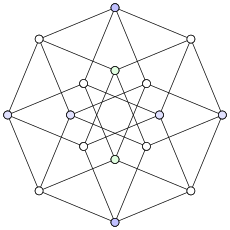
Другие конкретные графики, являющиеся графиками единичных расстояний, включают в себяграфик Петерсена , граф Хивуда , колеса график $W_{7}$ (единственный круговой граф, представляющий собой граф единичных расстояний), и веретено Мозера и граф Голомба (маленькие графы расстояний из 4-х хроматических единиц). Все обобщенные графы Петерсена , такие как изображенный граф Мёбиуса – Кантора , являются нестрогими графами единичных расстояний.

Спичечные графы — это частный случай графов единичных расстояний, в которых ребра не пересекаются. Любой спичечный граф представляет собой планарный граф , но некоторые в противном случае плоские графы единичных расстояний (например, веретено Мозера) имеют пересечение в каждом представлении в виде графа единичных расстояний. Кроме того, в контексте графиков единичных расстояний термин «планарный» следует использовать с осторожностью, поскольку некоторые авторы используют его для обозначения плоскости, в которой определяются единичные расстояния, а не для запрета на пересечения. Пенни -графы представляют собой еще более частный случай графов с единичными расстояниями и спичечных графов, в которых каждая несмежная пара вершин находится на расстоянии более одной единицы друг от друга.

Характеристики

Количество ребер

См. Также: Проблема различимых расстояний Эрдеша

Нерешенная задача по математике :

Сколько единичных расстояний можно определить с помощью набора $n$ баллы?

(еще нерешенные задачи по математике)

Пол Эрдеш ( 1946 ) поставил задачу оценить, сколько пар точек в наборе $n$ точки могут находиться на единичном расстоянии друг от друга. С точки зрения теории графов, вопрос заключается в том, насколько плотным может быть граф единичных расстояний, и публикация Эрдёша по этому вопросу была одной из первых работ в экстремальной теории графов . Графы гиперкуба и графы Хэмминга дают нижнюю границу количества единичных расстояний, пропорциональную $n\log n.$ Рассматривая точки в квадратной сетке с тщательно выбранным интервалом, Эрдеш нашел улучшенную нижнюю границу формы $$n^{1+c/\log \log n}$$для постоянного $c$и предложил 500 долларов за доказательство того, что число единичных расстояний также может быть ограничено сверху функцией такого вида. Самая известная верхняя оценка этой задачи равна $${\sqrt[{3}]{\frac {29n^{4}}{4}}}\approx 1.936n^{4/3}.$$ Эту оценку можно рассматривать как подсчет инцидентностей между точками и единичными кругами, и она тесно связана с неравенством числа пересечений и теоремой Семереди-Троттера об инцидентности между точками и прямыми.

Для небольших значений $n$ известно точное максимальное количество возможных ребер. Для $n=2,3,4,\dots$ это количество ребер:

1, 3, 5, 7, 9, 12, 14, 18, 20, 23, 27, 30, 33, ... (последовательность A186705 в OEIS )

Запрещенные подграфы

Если данный граф $G$ не является нестрогим графом единичных расстояний, как и любой суперграф $H$ из $G$. Похожая идея работает для графов со строгими единичными расстояниями, но с использованием концепции индуцированного подграфа — подграфа, сформированного из всех ребер между парами вершин в заданном подмножестве вершин. Если $G$ не является строгим графом единичных расстояний, то и любой другой $H$ у которого есть $G$ как индуцированный подграф. Из-за этих отношений между тем, является ли подграф или его суперграф графом единичных расстояний, можно описывать графы единичных расстояний с помощью их запрещенных подграфов . Это минимальные графы, не являющиеся графами единичных расстояний данного типа. Их можно использовать для определения того, является ли данный граф $G$ представляет собой граф единичных расстояний любого типа. $G$ является нестрогим графом единичных расстояний тогда и только тогда, когда $G$ не является суперграфом запрещенного графа для нестрогих графов единичных расстояний. $G$ является строгим графом единичных расстояний тогда и только тогда, когда $G$ не является индуцированным суперграфом запрещенного графа для графов строгих единичных расстояний.

Как для нестрогих, так и для строгих графов единичных расстояний запрещенные графы включают в себя как полный граф, так и полный граф. $K_{4}$ и полный двудольный граф $K_{2,3}$. Для $K_{2,3}$, где бы ни находились вершины на двухвершинной стороне этого графа, на единицу расстояния от них существует не более двух позиций для размещения трех других вершин, поэтому невозможно разместить все три вершины в разных точках. Это единственные два запрещенных графа для нестрогих графов единичных расстояний, содержащих до пяти вершин; существует шесть запрещенных графов с числом вершин до семи и 74 на графах до девяти вершин. Поскольку склеивание двух графов единичных расстояний (или их подграфов) в вершине создает строгие (соответственно нестрогие) графы единичных расстояний, каждый запрещенный граф является двусвязным графом , который не может быть сформирован в результате этого процесса склеивания.

График колеса $W_{7}$ может быть реализован как строгий граф единичных расстояний, шесть вершин которого образуют единичный правильный шестиугольник , а седьмая - в центре шестиугольника. Удаление одного из ребер из центральной вершины создает подграф, который по-прежнему имеет ребра единичной длины, но не является строгим графом единичных расстояний. Размещение его вершин в правильном шестиугольнике — единственный способ ( с точностью до конгруэнтности ) разместить вершины в разных местах, так что соседние вершины находятся на единичном расстоянии друг от друга, и это размещение также помещает две конечные точки недостающего ребра на единичное расстояние. . Таким образом, это запрещенный граф для графов строгих единичных расстояний: но не один из шести запрещенных графов для нестрогих графов единичных расстояний. Другие примеры графов, которые являются нестрогими графами единичных расстояний, но не являются строгими графами единичных расстояний, включают граф, образованный удалением внешнего ребра из $W_{7}$и граф с шестью вершинами, образованный из треугольной призмы путем удаления ребра из одного из ее треугольников.

Алгебраические числа и жесткость

Основная статья: теорема Бекмана – Куорлза

Для каждого алгебраического числа $\alpha$, можно построить граф единичных расстояний $G$ в котором некоторая пара вершин находится на расстоянии $\alpha$ во всех представлениях на единичном расстоянии $G$. Из этого результата следует конечная версия теоремы Бекмана–Куорлза : для любых двух точек $p$ и $q$ на расстоянии $\alpha$ друг от друга существует конечный жесткий граф единичных расстояний, содержащий $p$ и $q$ такое, что любое преобразование плоскости, сохраняющее единичные расстояния в этом графе, также сохраняет расстояние между $p$ и $q$. Полная теорема Бекмана-Куорлза утверждает, что единственные преобразования евклидовой плоскости (или многомерного евклидова пространства), сохраняющие единичные расстояния, - это изометрии . Аналогично, для бесконечного графа единичных расстояний, порожденного всеми точками плоскости, все автоморфизмы графа сохраняют все расстояния на плоскости, а не только единичные расстояния.

Если $\alpha$ — алгебраическое число с модулем 1, не являющееся корнем из единицы , то целые комбинации степеней $\alpha$ образуют конечно порожденную подгруппу комплексных аддитивной группы чисел , граф единичных расстояний которой имеет бесконечную степень . Например, $\alpha$ может быть выбран в качестве одного из двух комплексных корней многочлена $z^{4}-z^{3}-z^{2}-z+1$, создавая граф единичных расстояний бесконечной степени с четырьмя генераторами.

Раскраска

Основная статья: Задача Хадвигера – Нельсона

Нерешенная задача по математике :

Каково максимально возможное хроматическое число графа единичных расстояний?

(еще нерешенные задачи по математике)

Проблема Хадвигера -Нельсона касается хроматического числа графов единичных расстояний, а точнее, бесконечного графа единичных расстояний, образованного из всех точек евклидовой плоскости. По теореме де Брейна-Эрдёша , которая предполагает аксиому выбора , это эквивалентно запросу наибольшего хроматического числа графа конечных единичных расстояний. Существуют графы единичных расстояний, требующие пяти цветов в любой правильной раскраске. и все графики единичных расстояний можно раскрасить не более чем в семь цветов.

Семираскраска бесконечного графа единичных расстояний, сформированного из всех точек плоскости, и четыреххроматическое веретено Мозера, встроенное в граф единичных расстояний.

Отвечая на другой вопрос Пола Эрдеша, можно сказать, что для графиков единичных расстояний без треугольников может потребоваться четыре цвета.

Перечисление

Количество графиков строгих единичных расстояний на $n\geq 4$ помеченных вершин не более $${\binom {n(n-1)}{2n}}=O\left(2^{{\bigl (}4+o(1){\bigr )}n\log _{2}n}\right),$$как это выражается с использованием обозначения «большое О» и обозначения «маленькое О».

Обобщение на более высокие измерения

Определение графа единичных расстояний естественным образом можно обобщить на любое многомерное евклидово пространство . В трех измерениях графики единичных расстояний $n$ баллы имеют не более $n^{3/2}\beta (n)$ края, где $\beta$ — очень медленно растущая функция, связанная с обратной функцией Аккермана . Этот результат приводит к аналогичной оценке количества ребер трехмерных графов относительной окрестности . В четырех или более измерениях любой полный двудольный граф представляет собой граф единичных расстояний, реализованный путем размещения точек на двух перпендикулярных окружностях с общим центром, поэтому графы единичных расстояний могут быть плотными графами . Формулы перечисления для графов единичных расстояний обобщаются на более высокие измерения и показывают, что в измерениях четыре или более количество строгих графов единичных расстояний намного больше, чем количество подграфов графов единичных расстояний.

Любой конечный граф может быть встроен как граф единичных расстояний в достаточно высокой размерности. Некоторым графам могут потребоваться совершенно разные измерения для встраивания в виде нестрогих графов единичных расстояний и строгих графов единичных расстояний. Например, $2n$ вершин Граф короны может быть встроен в четыре измерения как нестрогий граф единичных расстояний (то есть так, чтобы все его ребра имели единичную длину). Однако для этого требуется как минимум $n-2$ измерения должны быть встроены в строгий граф единичных расстояний, чтобы его ребра были единственными парами единичных расстояний. Размерность, необходимая для реализации любого данного графа как строгого единичного графа, не более чем в два раза превышает его максимальную степень.

Вычислительная сложность

Построение графа единичных расстояний из его точек является важным шагом для других алгоритмов поиска конгруэнтных копий некоторого шаблона в большем наборе точек. Эти алгоритмы используют эту конструкцию для поиска позиций-кандидатов, где присутствует одно из расстояний в шаблоне, а затем используют другие методы для проверки остальной части шаблона для каждого кандидата. метод Матушека (1993) : К этой проблеме можно применить получение алгоритма для поиска графика единичных расстояний набора плоских точек во времени $n^{4/3}2^{O(\log ^{*}n)}$ где $\log ^{*}$ — медленно растущая функция повторного логарифма .

NP -трудно (а точнее, полно для экзистенциальной теории действительных чисел ) проверить, является ли данный граф (строгим или нестрогим) графом единичных расстояний на плоскости. Также NP-полно определить, имеет ли планарный граф единичных расстояний гамильтонов цикл , даже если все вершины графа имеют известные целочисленные координаты.

Ссылки

Источники

• Агостон, Питер; Pálvölgyi, Dömötör (April 2022), "An improved constant factor for the unit distance problem", Studia Scientiarum Mathematicarum Hungarica , 59 (1), Akademiai Kiado Zrt.: 40–57, arXiv : 2006.06285 , doi : 10.1556/012.2022.01517 , S2CID   218479287
• Алон, Нога ; Купавский, Андрей (2014), «Два понятия графов единичных расстояний» (PDF) , Журнал комбинаторной теории , Серия A, 125 : 1–17, doi : 10.1016/j.jcta.2014.02.006 , MR   3207464 , S2CID   12043969
• Бекман, Ф.С.; Куорлз, Д.А. младший (1953), «Об изометриях евклидовых пространств», Труды Американского математического общества , 4 (5): 810–815, doi : 10.2307/2032415 , JSTOR   2032415 , MR   0058193
• Брасс, Питер (2002), «Задачи комбинаторной геометрии в распознавании образов», Discrete & Computational Geometry , 28 (4): 495–510, doi : 10.1007/s00454-002-2884-3 , MR   1949897
• Брауэр, Андрис Э .; Хемерс, Виллем Х. (2012), Спектры графов , Universitext, Нью-Йорк: Springer, стр. 178, номер домена : 10.1007/978-1-4614-1939-6 , ISBN.  978-1-4614-1938-9 , МР   2882891
• Карми, Пас; Дуймович, Вида ; Морен, Пэт ; Вуд, Дэвид Р. (2008), «Различные расстояния в графических рисунках» , Electronic Journal of Combinatorics , 15 (1): Research Paper 107, arXiv : 0804.3690 , doi : 10.37236/831 , MR   2438579 , S2CID   2955082
• Чан, Тимоти М .; Чжэн, Да Вэй (2022), «Задача Хопкрофта, брейт-звезда, 2-мерный дробный каскад и деревья решений», в Наоре, Джозефе (Сеффи); Бухбиндер, Нив (ред.), Труды симпозиума ACM-SIAM 2022 по дискретным алгоритмам, SODA 2022, Виртуальная конференция / Александрия, Вирджиния, США, 9–12 января 2022 г. , Общество промышленной и прикладной математики, стр. 190– 210, arXiv : 2111.03744 , doi : 10.1137/1.9781611977073.10 , S2CID   243847672
• Чилакамарри, Киран Б. (1995), «4-хроматический граф единичных расстояний без треугольников», Geombinatorics , 4 (3): 64–76, MR   1313386
• Чилакамарри, Киран Б.; Махони, Кэролайн Р. (1995), «Максимальные и минимальные запрещенные графы единичных расстояний на плоскости», Бюллетень Института комбинаторики и ее приложений , 13 : 35–43, MR   1314500 , цитируется по Globus & Parshall (2020). )
• Кларксон, Кеннет Л .; Эдельсбруннер, Герберт ; Гибас, Леонидас Дж .; Шарир, Миша ; Вельцль, Эмо (1990), «Оценки комбинаторной сложности расположения кривых и сфер», Дискретная и вычислительная геометрия , 5 (2): 99–160, doi : 10.1007/BF02187783 , MR   1032370 , S2CID   28143698
• де Грей, Обри DNJ (2018), «Хроматическое число плоскости не менее 5», Geombinatorics , 28 : 5–18, arXiv : 1804.02385 , MR   3820926
• Эрдеш, Пол (1946), «О множествах расстояний $n$ точки», American Mathematical Monthly , 53 (5): 248–250, doi : 10.2307/2305092 , JSTOR   2305092.
• Эрдеш, Пол ; Харари, Фрэнк ; Тутте, Уильям Т. (1965), «О размерности графа» (PDF) , Mathematika , 12 (2): 118–122, doi : 10.1112/S0025579300005222 , hdl : 2027.42/152495 , MR   0188096
• Эрдеш, Пол ; Симоновиц, Миклош (1980), «О хроматическом числе геометрических графов», Ars Combinatoria , 9 : 229–246 , цитируется Сойфером (2008 , стр. 97).
• Эрдеш, Пол (1990), «Некоторые из моих любимых нерешенных задач», Бейкер, А.; Боллобас, Б.; Хайнал, А. (ред.), Дань памяти Полу Эрдешу , Cambridge University Press, стр. 467–478, ISBN  0-521-38101-0 , МР   1117038 ; см., в частности, стр. 475
• Гербрахт, Эберхард Х.-А. (2009), Вложения графа Хивуда на одиннадцать единиц расстояния , arXiv : 0912.5395 , Bibcode : 2009arXiv0912.5395G
• Джервасио, Северино В.; Лим, Иветт Ф.; Маэхара, Хироши (2008), «Плоские графы единичных расстояний, имеющие плоское дополнение единичных расстояний», Discrete Mathematics , 308 (10): 1973–1984, doi : 10.1016/j.disc.2007.04.050
• Глобус, Эйдан; Паршалл, Ганс (2020), «Малые графы единичных расстояний на плоскости», Бюллетень Института комбинаторики и ее приложений , 90 : 107–138, arXiv : 1905.07829 , MR   4156400
• Гриффитс, Мартин (июнь 2019 г.), «103.27 Свойство определенного графа единичных расстояний», The Mathematical Gazette , 103 (557): 353–356, doi : 10.1017/mag.2019.74 , S2CID   233361952
• Хорват, Борис; Писански, Томаж (2010), «Продукты графов единичных расстояний», Дискретная математика , 310 (12): 1783–1792, doi : 10.1016/j.disc.2009.11.035 , MR   2610282
• Хьюсон, Марк Л.; Сен, Арунабха (1995), «Алгоритмы планирования вещания для радиосетей», Конференция по военной связи, IEEE MILCOM '95 , том. 2, стр. 647–651, номер документа : 10.1109/MILCOM.1995.483546 , ISBN.  0-7803-2489-7 , S2CID   62039740
• Итай, Алон; Пападимитриу, Христос Х .; Шварцфитер, Хайме Луис (1982), «Пути Гамильтона в сеточных графах», SIAM Journal on Computing , 11 (4): 676–686, CiteSeerX   10.1.1.383.1078 , doi : 10.1137/0211056 , MR   0677661
• Яромчик, Ежи В.; Туссен, Годфрид Т. (1992), «Графы относительной окрестности и их родственники», Proceedings of the IEEE , 80 (9): 1502–1517, doi : 10.1109/5.163414
• Лангин, Кэти (18 апреля 2018 г.), «Математик-любитель решает математическую задачу, возникшую десятилетиями» , Science
• Лаволле, Жереми; Свейнпол, Конрад Дж. (2022), «Ограничение количества ребер спичечных графов», SIAM Journal on Discrete Mathematics , 36 (1): 777–785, arXiv : 2108.07522 , doi : 10.1137/21M1441134 , MR   4399020 , S2CID   2371 42624
• Маэхара, Хироши (1991), «Расстояния в жестком графе единичных расстояний на плоскости», Discrete Applied Mathematics , 31 (2): 193–200, doi : 10.1016/0166-218X(91)90070-D
• Маэхара, Хироши (1992), «Расширение гибкой структуры единичных стержней до жесткой», Discrete Mathematics , 108 (1–3): 167–174, doi : 10.1016/0012-365X(92)90671-2 , MR   1189840
• Маэхара, Хироши; Рёдль, Войтех (1990), «О размерности представления графа с помощью графа единичных расстояний», Graphs and Combinatorics , 6 (4): 365–367, doi : 10.1007/BF01787703 , S2CID   31148911
• Матушек, Иржи (1993), «Поиск диапазона с помощью эффективных иерархических разрезов», Дискретная и вычислительная геометрия , 10 (2): 157–182, doi : 10.1007/BF02573972 , MR   1220545
• О'Доннелл, Пол (1995), «40-вершинный 4-хроматический граф расстояний без треугольников», Geombinatorics , 5 (1): 31–34, MR   1337155
• Пах, Янош ; Тардос, Габор (2005), «Запрещенные шаблоны и единичные расстояния», Митчелл, Джозеф С.Б.; Роте, Гюнтер (ред.), Труды 21-го симпозиума ACM по вычислительной геометрии, Пиза, Италия, 6-8 июня 2005 г. , Ассоциация вычислительной техники, стр. 1–9, doi : 10.1145/1064092.1064096 , MR   2460341 , S2CID   18752227
• Радченко, Даниил (2021), «Графы единичных расстояний и алгебраические целые числа», Дискретная и вычислительная геометрия , 66 (1): 269–272, doi : 10.1007/s00454-019-00152-4 , hdl : 21.11116/0000-0006- 9КФД-Э , МР   4270642 , С2КИД   119682489
• Шефер, Маркус (2013), «Реализуемость графов и связей», Пач, Янош (ред.), «Тридцать эссе по геометрической теории графов » , Springer, стр. 461–482, CiteSeerX   10.1.1.220.9651 , doi : 10.1007/ 978-1-4614-0110-0_24 , ISBN  978-1-4614-0109-4
• Сойфер, Александр (2008), Математическая книжка-раскраска , Springer-Verlag, ISBN  978-0-387-74640-1
• Спенсер, Джоэл ; Семереди, Эндре ; Троттер, Уильям Т. (1984), «Единичные расстояния в евклидовой плоскости», в Боллобасе, Бела (редактор), Теория графов и комбинаторика , Лондон: Academic Press, стр. 293–308, ISBN  978-0-12-111760-3 , МР   0777185
• Семереди, Эндре (2016), «Проблема единичного расстояния Эрдёша», в Нэше, Джон Форбс-младший ; Рассиас, Майкл Т. (ред.), Открытые задачи по математике , Чам, Швейцария: Springer, стр. 459–477, doi : 10.1007/978-3-319-32162-2_15 , MR   3526946
• Тышка, Аполониуш (2000), «Дискретные версии теоремы Бекмана-Куорлза», Mathematical Equations , 59 (1–2): 124–133, arXiv : math/9904047 , doi : 10.1007/PL00000119 , MR   1741475 , S2CID   14803 182
• Вормальд, Николас (1979), «4-хроматический граф со специальным рисунком плоскости», Журнал Австралийского математического общества , серия A, 28 (1): 1–8, doi : 10.1017/S1446788700014865 , MR   0541161 , S2CID   124067465
• Житник, Арьяна; Хорват, Борис; Писански, Томаж (2012), «Все обобщенные графы Петерсена являются графами единичных расстояний», Журнал Корейского математического общества , 49 (3): 475–491, doi : 10.4134/JKMS.2012.49.3.475 , MR   2953031

Внешние ссылки

• Венкатасубраманиан, Суреш, «Задача 39: расстояния между множествами точек в R». ² и Р ³ " , Проект "Открытые проблемы "
• Вайсштейн, Эрик В. , «График единичных расстояний» , MathWorld