Граф короны

Граф короны
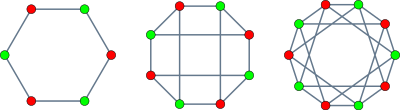Графы короны с шестью, восемью и десятью вершинами
Вершины	2 н
Края	п ( п – 1)
Радиус	$\left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{otherwise}}\end{array}}\right.$
Диаметр	$\left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{otherwise}}\end{array}}\right.$
Обхват	$\left\{{\begin{array}{ll}\infty &n\leq 2\\6&n=3\\4&{\text{otherwise}}\end{array}}\right.$
Хроматическое число	$\left\{{\begin{array}{ll}1&n=1\\2&{\text{otherwise}}\end{array}}\right.$
Характеристики	Дистанционно-транзитивный
Обозначения	$S_{n}^{0}$
Таблица графиков и параметров

В теории графов , разделе математики, коронный граф на 2 n вершинах — это неориентированный граф с двумя наборами вершин u 1 _, u 2 _, …, v _un } и { v ₁ , v ₂ , …, { _n } и с ребром от u _i до v _j всякий раз, когда i ≠ j .

Граф короны можно рассматривать как полный двудольный граф, ребра идеального паросочетания из которого удалены , как двудольное двойное накрытие , полного графа как тензорное произведение K _n × K ₂ , как дополнение декартова прямого произведение K _n и K ₂ , или как двудольный граф Кнезера H _{n ,1,} представляющий подмножества из 1 элемента и ( n – 1) - элементов набора из n - элементов, с ребром между двумя подмножествами, если одно из них содержится в другой.

Примеры

Граф короны с 6 вершинами образует цикл , а граф короны с 8 вершинами изоморфен графу куба .В двойной шестерке Шлефли , конфигурации из 12 линий и 30 точек в трехмерном пространстве, двенадцать линий пересекаются друг с другом по образцу коронного графа с 12 вершинами.

Характеристики

Биликическое покрытие десятивершинного коронного графа

Количество ребер в графе короны — это проническое число n ( n – 1) . Его ахроматическое число n в : можно найти полную раскраску , выбрав каждую пару { u _i , v _i } качестве одного из цветовых классов. Графы Короны симметричны и дистанционно транзитивны . Архидиакон и др. (2004) описывают разбиение ребер коронного графа на циклы одинаковой длины.

Граф короны с 2 n вершинами можно вложить в четырехмерное евклидово пространство таким образом, чтобы все его ребра имели единичную длину. Однако это вложение может также разместить некоторые несмежные вершины на расстоянии единицы друг от друга. Вложение, в котором ребра находятся на единичном расстоянии, а не-ребра не находятся на единичном расстоянии, требует как минимум n – 2 измерений. Этот пример показывает, что граф может потребовать очень разных измерений для представления в виде графа единичных расстояний и строгого графа единичных расстояний.

Минимальное количество полных двудольных подграфов, необходимых для покрытия ребер коронного графа (его двудольная размерность или размер минимального бикликового покрытия), равно

$\sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\},$

обратная функция центрального биномиального коэффициента .

Граф дополнений коронного графа с 2 n вершинами является декартовым произведением полных графов K ₂ ▢ K _n или, что то же самое, 2 × n ладейным графом .

Приложения

В этикете традиционное правило расстановки гостей за обеденным столом заключается в том, что мужчины и женщины должны чередоваться позами и ни одна семейная пара не должна сидеть рядом друг с другом. Договоренности, удовлетворяющие этому правилу, для группы, состоящей из n супружеских пар, можно описать как гамильтоновы циклы графа короны. Например, расположение вершин, показанное на рисунке, можно интерпретировать как схемы рассадки такого типа, на которых каждый муж и жена сидят как можно дальше друг от друга. Задача подсчета количества возможных рассадок или почти эквивалентная количество гамильтоновых циклов в коронном графе известно в комбинаторике как проблема управления ; для коронных графов с 6, 8, 10, ... вершинами количество (ориентированных) гамильтоновых циклов равно

2, 12, 312, 9600, 416880, 23879520, 1749363840, ... (последовательность A094047 в OEIS )

Графы короны можно использовать, чтобы показать, что алгоритмы жадной раскраски ведут себя плохо в худшем случае: если вершины графа короны представлены алгоритму в порядке u ₀ , v ₀ , u ₁ , v ₁ и т. д., то жадная раскраска использует n цветов, тогда как оптимальное количество цветов — два. Эту конструкцию приписывают Джонсону (1974) ; графы короны иногда называют графами Джонсона с обозначением J _n . Фюрер (1995) использует графы корон как часть конструкции, показывающей сложность аппроксимации задач раскраски.

Матушек (1996) использует расстояния в графах корон как пример метрического пространства , которое трудно встроить в нормированное векторное пространство .

Как показывают Миклавич и Поточник (2003) , коронные графы являются одним из небольшого числа различных типов графов, которые могут встречаться как дистанционно регулярные циркулянтные графы .

Агарвал и др. (1994) описывают полигоны, графы коронок которых являются графами видимости ; они используют этот пример, чтобы показать, что представление графов видимости как объединений полных двудольных графов не всегда может быть эффективным с точки зрения использования пространства.

Граф короны с 2 n вершинами, ребра которого ориентированы от одной стороны биразделения к другой, образует стандартный пример частично упорядоченного множества с порядковой размерностью   n .

Ссылки

• Агарвал, Панкадж К .; Алон, Нога ; Аронов, Борис ; Сури, Субхаш (1994), «Можно ли компактно представить графы видимости?», Discrete and Computational Geometry , 12 (1): 347–365, doi : 10.1007/BF02574385 , MR   1298916 .
• Архидиакон Д .; Дебовский, М.; Диниц, Дж .; Гавлас, Х. (2004), «Системы циклов в полном двудольном графе минус однофакторный», Discrete Mathematics , 284 (1–3): 37–43, doi : 10.1016/j.disc.2003.11.021 , MR   2071894 .
• Чаудхари, Амитабх; Вишванатан, Сундар (2001), «Алгоритмы аппроксимации ахроматического числа», Journal of Algorithms , 41 (2): 404–416, CiteSeerX   10.1.1.1.5562 , doi : 10.1006/jagm.2001.1192 , MR   1869259 , S2CID   98178 50 .
• де Кан, Доминик ; Грегори, Дэвид А.; Пуллман, Норман Дж. (1981), «Булев ранг матриц ноль-единица», в книге Кадоган, Чарльз К. (ред.), Proc. 3-я Карибская конференция по комбинаторике и информатике , факультет математики, Вест-Индский университет, стр. 169–173, MR   0657202 .
• Эрдеш, Пол ; Симоновиц, Миклош (1980), «О хроматическом числе геометрических графов» (PDF) , Ars Combinatoria , 9 : 229–246, MR   0582295 .
• Фюрер, Мартин (1995), «Улучшенные результаты твердости для аппроксимации хроматического числа», Труды 36-го ежегодного фонда компьютерных наук IEEE , стр. 414–421, doi : 10.1109/SFCS.1995.492572 , ISBN  978-0-8186-7183-8 , S2CID   195870010 .
• Джонсон, Д.С. (1974), "Поведение алгоритмов раскраски графов в наихудшем случае", Proc. 5-я Юго-Восточная конф. по комбинаторике, теории графов и информатике, Utilitas Mathematicae , Виннипег, стр. 513–527, MR   0389644. {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Кубале, М. (2004), Раскраски графов , Американское математическое общество, ISBN  978-0-8218-3458-9 , МР   2074481
• Матушек, Иржи (1996), «Об искажении, необходимом для встраивания конечных метрических пространств в нормированные пространства», Israel Journal of Mathematics , 93 (1): 333–344, doi : 10.1007/BF02761110 , MR   1380650 , S2CID   121050316 .
• Миклавич, Штефко; Поточник, Примож (2003), «Дистанционно-регулярные циркулянты», Европейский журнал комбинаторики , 24 (7): 777–784, doi : 10.1016/S0195-6698(03)00117-3 , MR   2009391 .

Внешние ссылки

• Вайсштейн, Эрик В. «График короны» . Математический мир .