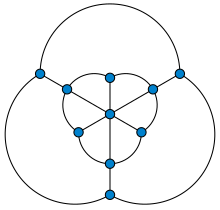
Граф Голомба

Граф Голомба
Граф Голомба
Назван в честь	Соломон В. Голомб
Вершины	10
Края	18
Автоморфизмы	6
Хроматическое число	4
Характеристики	многогранный ; единица расстояния ;
	Таблица графиков и параметров

В теории графов граф Голомба представляет собой многогранный граф с 10 вершинами и 18 ребрами . Он назван в честь Соломона В. Голомба , который построил его (с неплоским вложением ) как граф единичных расстояний , требующий четырех цветов в любой раскраске графа . Таким образом, как и более простое веретено Мозера , оно обеспечивает нижнюю оценку проблемы Хадвигера-Нельсона : для раскраски точек евклидовой плоскости так, чтобы каждый сегмент единичной прямой имел конечные точки разного цвета, требуется как минимум четыре цвета. ^[1]

Строительство [ править ]

4-раскраска графа Голомба, нарисованного в виде графа единичных расстояний

Метод построения графа Голомба как графа единичных расстояний путем рисования внешнего правильного многоугольника, соединенного с внутренним скрученным многоугольником или звездчатым многоугольником, также использовался для представлений на единичном расстоянии графа Петерсена и обобщенных графов Петерсена . ^[2] Как и в случае с веретеном Мозера, координаты вложения графа Голомба на единичное расстояние могут быть представлены в квадратичном поле $\mathbb {Q} [{\sqrt {33}}]$ . ^[3]

Дробная раскраска [ править ]

Дробное хроматическое число графа Голомба равно 10/3. Тот факт, что это число как минимум столь велико, следует из того, что граф имеет 10 вершин, не более трех из которых могут находиться в любом независимом множестве. Тот факт, что это число не превышает столь большое, следует из того факта, что можно найти 10 независимых трехвершинных множеств, таких, что каждая вершина находится ровно в трех из этих множеств.Это дробное хроматическое число меньше числа 7/2 для веретена Мозера и меньше дробного хроматического числа графа единичных расстояний на плоскости, которое ограничено значениями от 3,6190 до 4,3599. ^[4]

Ссылки [ править ]

^ Сойфер, Александр (2008), Математическая книжка-раскраска: математика раскраски и красочная жизнь ее создателей , Нью-Йорк: Springer, стр. 19, ISBN 978-0-387-74640-1
^ Житник, Арьяна; Хорват, Борис; Писански, Томаж (2012), «Все обобщенные графы Петерсена являются графами единичных расстояний», Журнал Корейского математического общества , 49 (3): 475–491, doi : 10.4134/JKMS.2012.49.3.475 , MR 2953031
^ Пегг, Эд-младший (21 декабря 2017 г.), «Шпиндели Мозера, графы Голомба и корень 33» , Демонстрационный проект Wolfram
^ Крэнстон, Дэниел В.; Раберн, Лэндон (2017), «Дробное хроматическое число плоскости», Combinatorica , 37 (5): 837–861, arXiv : 1501.01647 , doi : 10.1007/s00493-016-3380-3 , MR 3737371 , S2CID 4687673

Внешние ссылки [ править ]

Вайсштейн, Эрик В. «График Голомба» . Математический мир .

[soifer-1] Сойфер, Александр (2008), Математическая книжка-раскраска: математика раскраски и красочная жизнь ее создателей , Нью-Йорк: Springer, стр. 19, ISBN 978-0-387-74640-1

[zhp-2] Житник, Арьяна; Хорват, Борис; Писански, Томаж (2012), «Все обобщенные графы Петерсена являются графами единичных расстояний», Журнал Корейского математического общества , 49 (3): 475–491, doi : 10.4134/JKMS.2012.49.3.475 , MR 2953031

[pegg-3] Пегг, Эд-младший (21 декабря 2017 г.), «Шпиндели Мозера, графы Голомба и корень 33» , Демонстрационный проект Wolfram

[cranrab-4] Крэнстон, Дэниел В.; Раберн, Лэндон (2017), «Дробное хроматическое число плоскости», Combinatorica , 37 (5): 837–861, arXiv : 1501.01647 , doi : 10.1007/s00493-016-3380-3 , MR 3737371 , S2CID 4687673

[1]

[2]

[3]

[4]