Список геодезических многогранников и многогранников Гольдберга

Это список избранных геодезических многогранников и многогранников Гольдберга , двух бесконечных классов многогранников . Геодезические многогранники и многогранники Гольдберга являются двойственными друг другу. Геодезические и многогранники Гольдберга параметризуются целыми числами m и n , причем $m>0$ и $n\geq 0$ . T – число триангуляции, равное $T=m^{2}+mn+n^{2}$ .

икосаэдрический

м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	геодезический			Гольдберг
м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	Символы	Конвей	Изображение	Символы	Конвей	Изображение
1	0	1	я	12	30	20		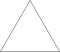{3,5} {3,5+} _1,0	я		{5,3} {5+,3} _1,0 ГП ₅ (1,0)	Д
2	0	4	я	42	120	80		{3,5+} _2,0	UI DCI		{5+,3} _2,0 ГП ₅ (2,0)	компакт-диск компакт-диск
3	0	9	я	92	270	180		{3,5+} _3,0	хI кти		{5+,3} _3,0 ГП ₅ (3,0)	yD ТКД
4	0	16	я	162	480	320		{3,5+} _4,0	ууи dccD		{5+,3} _4,0 ГП ₅ (4,0)	с ²Д
5	0	25	я	252	750	500		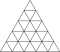{3,5+} _5,0	u5I u5I		{5+,3} _5,0 ГП ₅ (5,0)	c5D du5I
6	0	36	я	362	1080	720		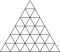{3,5+} _6,0	ух я dctkdI		{5+,3} _6,0 ГП ₅ (6,0)	со ctkD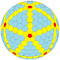
7	0	49	я	492	1470	980		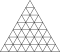{3,5+} _7,0	в в я dwrwdI		{5+,3} _7,0 ГП ₅ (7,0)	ш ш Д wrwD
8	0	64	я	642	1920	1280		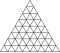{3,5+} _8,0	в ³я dcccdI		{5+,3} _8,0 ГП ₅ (8,0)	cccD
9	0	81	я	812	2430	1620		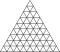{3,5+} _9,0	XXI кткти		{5+,3} _9,0 ГП ₅ (9,0)	ггД ткткД
10	0	100	я	1002	3000	2000		{3,5+} _10,0	уу5I уу5I		{5+,3} _10,0 ГП ₅ (10,0)	cc5D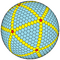
11	0	121	я	1212	3630	2420		{3,5+} _11,0	u11я u11я		{5+,3} _11,0 ГП ₅ (11,0)	c11D
12	0	144	я	1442	4320	2880		{3,5+} _12,0	запах Д dcctkD		{5+,3} _12,0 ГП ₅ (12,0)	ccyD cctkD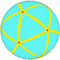
13	0	169	я	1692	5070	3380		{3,5+} _13,0	u13я u13я		{5+,3} _13,0 ГП ₅ (13,0)	c13D
14	0	196	я	1962	5880	3920		{3,5+} _14,0	уф в я dcw dI		{5+,3} _14,0 ГП ₅ (14,0)	пивоD
15	0	225	я	2252	6750	4500		{3,5+} _15,0	ИКБ u5ktI		{5+,3} _15,0 ГП ₅ (15,0)	c5yD c5tkD
16	0	256	я	2562	7680	5120		{3,5+} _16,0	округ Колумбия ⁴Из		{5+,3} _16,0 ГП ₅ (16,0)	ccccD
1	1	3	II	32	90	60		{3,5+} _1,1	в кД		{5+,3} _1,1 ГП ₅ (1,1)	yD из
2	2	12	II	122	360	240		{3,5+} _2,2	мука = dctI		{5+,3} _2,2 ГП ₅ (2,2)	Чехия CDKD
3	3	27	II	272	810	540		{3,5+} _3,3	xnI КТКД		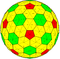{5+,3} _3,3 ГП ₅ (3,3)	yzD ткдкД
4	4	48	II	482	1440	960		{3,5+} _4,4	в ²nя dcctI		{5+,3} _4,4 ГП ₅ (4,4)	с ²зД cctI
5	5	75	II	752	2250	1500		{3,5+} _5,5	u5nI		{5+,3} _5,5 ГП ₅ (5,5)	c5zD
6	6	108	II	1082	3240	2160		{3,5+} _6,6	uxnI dctktI		{5+,3} _6,6 ГП ₅ (6,6)	циз Д ctkdkD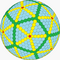
7	7	147	II	1472	4410	2940		{3,5+} _7,7	в в н я dwrwtI		{5+,3} _7,7 ГП ₅ (7,7)	в с D wrwdkD
8	8	192	II	1922	5760	3840		{3,5+} _8,8	в ³в dccckD		{5+,3} _8,8 ГП ₅ (8,8)	с ³z Д ccctI
9	9	243	II	2432	7290	4860		{3,5+} _9,9	xxxnI кткткД		{5+,3} _9,9 ГП ₅ (9,9)	yyzD ткткти
12	12	432	II	4322	12960	8640		{3,5+} _12,12	запах dccdktkD		{5+,3} _12,12 ГП ₅ (12,12)	ccyzD кктти я
14	14	588	II	5882	17640	11760		{3,5+} _14,14	уф в н я dcw w kD		{5+,3} _14,14 ГП ₅ (14,14)	cw в zD пиво
16	16	768	II	7682	23040	15360		{3,5+} _16,16	ууууни dcccctI		{5+,3} _16,16 ГП ₅ (16,16)	cccczD cccctI
2	1	7	III	72	210	140		{3,5+} _2,1	мы dwD		{5+,3} _2,1 ГП ₅ (2,1)	WD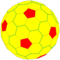
3	1	13	III	132	390	260		{3,5+} _3,1	v3,1I		{5+,3} _3,1 ГП ₅ (3,1)	w3,1D
3	2	19	III	192	570	380		{3,5+} _3,2	v3I		{5+,3} _3,2 ГП ₅ (3,2)	w3D
4	1	21	III	212	630	420		{3,5+} _4,1	dwtI		{5+,3} _4,1 ГП ₅ (4,1)	неделя
4	2	28	III	282	840	560		{3,5+} _4,2	вни dwtI		{5+,3} _4,2 ГП ₅ (4,2)	вдкД
4	3	37	III	372	1110	740		{3,5+} _4,3	v4I		{5+,3} _4,3 ГП ₅ (4,3)	w4D
5	1	31	III	312	930	620		{3,5+} _5,1	u5,1I		{5+,3} _5,1 ГП ₅ (5,1)	w5,1D
5	2	39	III	392	1170	780		{3,5+} _5,2	u5,2I		{5+,3} _5,2 ГП ₅ (5,2)	w5,2D
5	3	49	III	492	1470	980		{3,5+} _5,3	вви WWD		{5+,3} _5,3 ГП ₅ (5,3)	WWD
6	2	52	III	522	1560	1040		{3,5+} _6,2	v3,1uI		{5+,3} _6,2 ГП ₅ (6,2)	w3,1cD
6	3	63	III	632	1890	1260		{3,5+} _6,3	vx1 dwdktI		{5+,3} _6,3 ГП ₅ (6,3)	широкий wtkD
8	2	84	III	842	2520	1680		{3,5+} _8,2	поставь это каналI		{5+,3} _8,2 ГП ₅ (8,2)	раноD вкдкД
8	4	112	III	1122	3360	2240		{3,5+} _8,4	вууи dwccD		{5+,3} _8,4 ГП ₅ (8,4)	ВККД
11	2	147	III	1472	4410	2940		{3,5+} _11,2	ввни dwwtI		{5+,3} _11,2 ГП ₅ (11,2)	ИБС
12	3	189	III	1892	5670	3780		{3,5+} _12,3	vxnI dwtktktI		{5+,3} _12,3 ГП ₅ (12,3)	визД wtktI
10	6	196	III	1962	5880	3920		{3,5+} _10,6	ввуI dwwcD		{5+,3} _10,6 ГП ₅ (10,6)	WWCD
12	6	252	III	2522	7560	5040		{3,5+} _12,6	vxu1 dwctkD		{5+,3} _12,6 ГП ₅ (12,6)	cywD wctkD
16	4	336	III	3362	10080	6720		{3,5+} _16,4	годI dwcctI		{5+,3} _16,4 ГП ₅ (16,4)	wcczD wcctI
14	7	343	III	3432	10290	6860		{3,5+} _14,7	v v vI dwrwwD		{5+,3} _14,7 ГП ₅ (14,7)	ш ш шд врввД
15	9	441	III	4412	13230	8820		{3,5+} _15,9	vvxI dwwtkD		{5+,3} _15,9 ГП ₅ (15,9)	wwxD wwtkD
16	8	448	III	4482	13440	8960		{3,5+} _16,8	ух ты dwcccD		{5+,3} _16,8 ГП ₅ (16,8)	wcccD
18	1	343	III	3432	10290	6860		{3,5+} _18,1	ввви дауууД		{5+,3} _18,1 ГП ₅ (18,1)	wwwD
18	9	567	III	5672	17010	11340		{3,5+} _18,9	vxxI dwtktkD		{5+,3} _18,9 ГП ₅ (18,9)	гггг wtktkD
20	12	784	III	7842	23520	15680		{3,5+} _20,12	ух ты dwwccD		{5+,3} _20,12 ГП ₅ (20,12)	WWCCD
20	17	1029	III	10292	30870	20580		{3,5+} _20,17	вввни ооооооооооооооооооооооо		{5+,3} _20,17 ГП ₅ (20,17)	wwwzD wwwdkD
28	7	1029	III	10292	30870	20580		{3,5+} _28,7	в в вни dwrwwdkD		{5+,3} _28,7 ГП ₅ (28,7)	в ж вжд врввдкД

Октаэдрический

м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	геодезический			Гольдберг
м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	Символы	Конвей	Изображение	Символы	Конвей	Изображение
1	0	1	я	6	12	8		{3,4} {3,4+} _1,0	ТО		{4,3} {4+,3} _1,0 ГП ₄ (1,0)	С
2	0	4	я	18	48	32		{3,4+} _2,0	DCC DCC		{4+,3} _2,0 ГП ₄ (2,0)	СС СС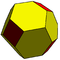
3	0	9	я	38	108	72		{3,4+} _3,0	ktO		{4+,3} _3,0 ГП ₄ (3,0)	ткС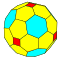
4	0	16	я	66	192	128		{3,4+} _4,0	ууО DCCC		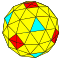{4+,3} _4,0 ГП ₄ (4,0)	CCC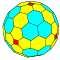
5	0	25	я	102	300	200		{3,4+} _5,0	и5О		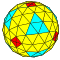{4+,3} _5,0 ГП ₄ (5,0)	c5C
6	0	36	я	146	432	288		{3,4+} _6,0	uxO dctkdO		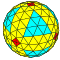{4+,3} _6,0 ГП ₄ (6,0)	CYC ctkC
7	0	49	я	198	588	392		{3,4+} _7,0	вода		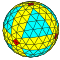{4+,3} _7,0 ГП ₄ (7,0)	wrwO
8	0	64	я	258	768	512		{3,4+} _8,0	ууууу dcccC		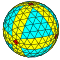{4+,3} _8,0 ГП ₄ (8,0)	cccC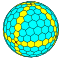
9	0	81	я	326	972	648		{3,4+} _9,0	ххО ктктО		{4+,3} _9,0 ГП ₄ (9,0)	ггС tktkC
1	1	3	II	14	36	24		{3,4+} _1,1	кС		{4+,3} _1,1 ГП ₄ (1,1)	к
2	2	12	II	50	144	96		{3,4+} _2,2	Великобритания dctO		{4+,3} _2,2 ГП ₄ (2,2)	Чехия CTO
3	3	27	II	110	324	216		{3,4+} _3,3	КТКС		{4+,3} _3,3 ГП ₄ (3,3)	ТКТО
4	4	48	II	194	576	384		{3,4+} _4,4	УунО dcctO		{4+,3} _4,4 ГП ₄ (4,4)	cczC cctO
2	1	7	III	30	84	56		{3,4+} _2,1	vO ДВК		{4+,3} _2,1 ГП ₄ (2,1)	Туалет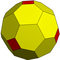

Тетраэдрический

м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	геодезический			Гольдберг
м	н	Т	Сорт	Вершины (геодезический) Лица (Гольдберг)	Края	Лица (геодезический) Вершины (Гольдберг)	Лицо треугольник	Символы	Конвей	Изображение	Символы	Конвей	Изображение
1	0	1	я	4	6	4		{3,3} {3,3+} _1,0	Т		{3,3} {3+,3} _1,0 ГП ₃ (1,0)	Т
1	1	3	II	8	18	12		{3,3+} _1,1	кТ кТ		{3+,3} _1,1 ГП ₃ (1,1)	тТ тТ
2	0	4	я	10	24	16		{3,3+} _2,0	ДКТ ДКТ		{3+,3} _2,0 ГП ₃ (2,0)	КТ КТ
3	0	9	я	20	54	36		{3,3+} _3,0	кТ		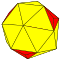{3+,3} _3,0 ГП ₃ (3,0)	ТС
4	0	16	я	34	96	64		{3,3+} _4,0	тритон dccT		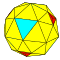{3+,3} _4,0 ГП ₃ (4,0)	ККТ
5	0	25	я	52	150	100		{3,3+} _5,0	u5T		{3+,3} _5,0 ГП ₃ (5,0)	с5Т
6	0	36	я	74	216	144		{3,3+} _6,0	UXT dctkdT		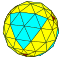{3+,3} _6,0 ГП ₃ (6,0)	цит ctkT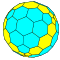
7	0	49	я	100	294	196		{3,3+} _7,0	врвТ водаТ		{3+,3} _7,0 ГП ₃ (7,0)	wrwT
8	0	64	я	130	384	256		{3,3+} _8,0	в ³Т dcccdT		{3+,3} _8,0 ГП ₃ (8,0)	с ³Т cccT
9	0	81	я	164	486	324		{3,3+} _9,0	ххТ ктктТ		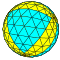{3+,3} _9,0 ГП ₃ (9,0)	ггТ ткткТ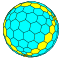
3	3	27	II	56	162	108		{3,3+} _3,3	кткТ		{3+,3} _3,3 ГП ₃ (3,3)	тктТ
2	1	7	III	16	42	28		{3,3+} _2,1	dwT		{3+,3} _2,1 ГП ₅ (2,1)	wT