Пентакис икосододекаэдр
| Пентакис икосододекаэдр | |
|---|---|
 | |
| Тип | Геодезический многогранник (2,0) |
| Лица | 80 треугольников (20 равносторонних ; 60 равнобедренных ) |
| Края | 120 (2 типа) |
| Вершины | 42 (2 типа) |
| Конфигурация вершин | (12) 3 5 (30) 3 6 |
| Обозначение Конвея | k5aD = dcD = uI |
| Группа симметрии | Икосаэдрический ( I h ) |
| Двойной многогранник | Додекаэдр со скошенной кромкой |
| Характеристики | выпуклый |
| Сеть | |
 | |
В геометрии пентакис икосододекаэдр или разделенный икосаэдр представляет собой выпуклый многогранник с 80 треугольными гранями , 120 ребрами и 42 вершинами . Это двойник усеченного ромботриаконтаэдра ( додекаэдра с фаской ).
Строительство
[ редактировать ]Его название происходит от топологической конструкции икосододекаэдра с оператором kis, примененным к пятиугольным граням. В этой конструкции предполагается, что все вершины находятся на одинаковом расстоянии от центра, в то время как в целом икосаэдральная симметрия может сохраняться даже при условии, что 12 вершин пятого порядка находятся на другом расстоянии от центра, чем остальные 30.
Его также можно топологически построить из икосаэдра , разделив каждую треугольную грань на 4 треугольника путем добавления средних ребер вершин. Из этой конструкции все 80 треугольников будут равносторонними, но грани будут компланарными .
| Конвей | (ты 2 )я | (к5)ай |
|---|---|---|
| Изображение |  | 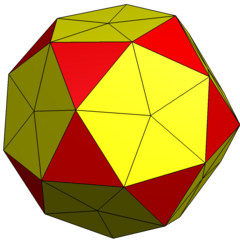 |
| Форма | 2-частотный разделенный икосаэдр | Пентакис икосододекаэдр |
Связанные многогранники
[ редактировать ]- Додекаэдр Пентакиса немного меньшего размера — каталонское тело , имеющее 60 граней равнобедренного треугольника, 90 ребер (2 типа) и 32 вершины (2 типа).
- Трипентакис икосододекаэдр, клитопа икосододекаэдра, можно получить, подняв низкие пирамиды на каждой равносторонней треугольной грани пентакис икосододекаэдра. Он имеет 120 граней равнобедренного треугольника (2 типа), 180 ребер (3 типа) и 62 вершины (3 типа).
- Невыпуклый малый икосихемидодекаэдр выглядит как икосододекаэдр пентакиса с перевернутыми пятиугольными пирамидами, сходящимися в центре многогранника.

]]== Связанные многогранники ==
Он представляет собой внешнюю оболочку вершинно-центрированной ортогональной проекции многогранника 600-ячеечного , одного из шести выпуклых правильных 4-многогранников , в 3 измерения.
См. также
[ редактировать ]Ссылки
[ редактировать ]- Джордж В. Харт , Скульптура на основе пропеллеризованных многогранников , Proceedings of MOSAIC 2000, Сиэтл, Вашингтон, август 2000 г., стр. 61–70 [1]
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5
- Глава 21: Именование архимедовых и каталанских многогранников и мозаик (стр. 284)
- Веннингер, Магнус (1979), Сферические модели , Издательство Кембриджского университета , ISBN 978-0-521-29432-4 , MR 0552023 Дувр 1999 г. ISBN 978-0-486-40921-4
Внешние ссылки
[ редактировать ]- Генератор многогранников VTML Попробуйте «k5aD» ( обозначение многогранника Конвея )



