Геодезический многогранник

Геодезический многогранник – это выпуклый многогранник, составленный из треугольников . Обычно они имеют икосаэдрическую симметрию , то есть имеют 6 треугольников в вершине , за исключением 12 вершин, в которых по 5 треугольников. Они являются двойственными соответствующим многогранникам Гольдберга , все из которых, кроме самого маленького (правильного додекаэдра ), имеют в основном шестиугольные грани.

Геодезические многогранники являются хорошим приближением сферы для многих целей и появляются во многих различных контекстах. Самыми известными могут быть геодезические купола , полусферические архитектурные конструкции, спроектированные Бакминстером Фуллером , в честь которых названы геодезические многогранники. Геодезические сетки, используемые в геодезии, также имеют геометрию геодезических многогранников. Капсиды имеют некоторых вирусов форму геодезических многогранников. ^[1]^[2] а некоторые пыльцевые зерна имеют в основе геодезические многогранники. ^[3] Молекулы фуллеренов имеют форму многогранников Гольдберга . Геодезические многогранники доступны в виде геометрических примитивов в пакете программ для 3D-моделирования Blender , который называет их икосферами : они являются альтернативой УФ-сфере , имеющей более регулярное распределение. ^[4]^[5] Конструкция Гольдберга – Кокстера представляет собой расширение представлений, лежащих в основе геодезических многогранников.

3 конструкции для {3,5+} _6,0



Икосаэдр и связанные с ним многогранники симметрии можно использовать для определения высокого геодезического многогранника путем разделения треугольных граней на меньшие треугольники и проецирования всех новых вершин на сферу. Многоугольные грани более высокого порядка можно разделить на треугольники, добавив новые вершины с центром на каждой грани. Новые грани сферы не являются равносторонними треугольниками , но имеют примерно одинаковую длину ребра. Все вершины имеют валентность 6, за исключением 12 вершин с валентностью 5.

Строительство {3,5+} _3,3

Геодезические подразделения также можно выполнить из расширенного додекаэдра , разделив пятиугольники на треугольники с центральной точкой и разделив их на основе этого.

Строительство {3,5+} _6,3

Киральные многогранники с многоугольными гранями более высокого порядка могут быть дополнены центральными точками и новыми треугольными гранями. Эти треугольники затем можно разделить на более мелкие треугольники для новых геодезических многогранников. Все вершины имеют валентность 6, за исключением 12, центрированных в исходных вершинах, которые имеют валентность 5.

Геодезические обозначения

В Магнуса Веннингера многогранникам сферических моделях даны геодезические обозначения в виде {3, q +} _{b , c} , где {3, q } — символ Шлефли для правильного многогранника с треугольными гранями и q -валентными вершинами. Символ + указывает на валентность увеличиваемых вершин. b , c представляют собой описание подразделения, где 1,0 представляет базовую форму. Существует 3 класса симметрии форм: {3,3+} _1,0 для тетраэдра , {3,4+} _1,0 для октаэдра и {3,5+} _1,0 для икосаэдра .

Двойственное обозначение многогранников Гольдберга — { q +,3} _{b , c} , с вершинами валентности 3, с q -угольными и шестиугольными гранями. Существует 3 класса симметрии форм: {3+,3} _1,0 для тетраэдра , {4+,3} _1,0 для куба и {5+,3} _1,0 для додекаэдра .

Значения b , c делятся на три класса:

Класс I (b=0 или c=0): {3, q +} _{b ,0} или {3, q +} _{0, b} представляют собой простое деление, в котором исходные ребра делятся на b подребер.

Класс II (b=c): {3, q +} _{b , b} легче увидеть из двойственного многогранника { q ,3} с q -угольными гранями, сначала разделенными на треугольники с центральной точкой, а затем все ребра разделены. на b подребер.

Класс III : {3, q +} _{b , c} имеют ненулевые неравные значения для b , c и существуют в киральных парах. Для b > c мы можем определить ее как правую форму, а c > b — как левую форму.

Подразделения класса III здесь не просто совпадают с исходными краями. Подсетки можно извлечь, взглянув на треугольную мозаику , поместив большой треугольник поверх вершин сетки и пройдя по дорожкам из одной вершины. b шаги в одном направлении и поворот по часовой стрелке или против часовой стрелки, а затем еще один шаг c к следующей. первичная вершина.

Например, икосаэдр {3,5+} _1,0 , а пентакис додекаэдр {3,5+} _1,1 рассматривается как правильный додекаэдр с пятиугольными гранями, разделенными на 5 треугольников.

Первичная грань подразделения называется главным многогранным треугольником (ППТ) или структурой разбивки . Расчет одного PPT позволяет создать всю фигуру.

Частота b многогранника определяется суммой ν = c + . геодезического Гармоника представляет собой подчастоту и может быть любым целым делителем ν . Класс II всегда имеет гармонику 2, поскольку ν = 2 b .

Число триангуляции T = b ² + до н.э. + с ². Это число, умноженное на количество исходных граней, показывает, сколько треугольников будет в новом многограннике.

**PPT с частотой 8**

Элементы

Количество элементов задается номером триангуляции. $T=b^{2}+bc+c^{2}$ . Два разных геодезических многогранника могут иметь одинаковое количество элементов, например, {3,5+} _5,3 и {3,5+} _7,0 оба имеют T = 49.

Симметрия	икосаэдрический	Октаэдрический	Тетраэдрический
База	Икосаэдр {3,5} = {3,5+} _1,0	Октаэдр {3,4} = {3,4+} _1,0	Тетраэдр {3,3} = {3,3+} _1,0
Изображение
Символ	{3,5+} _{б , в}	{3,4+} _{б , в}	{3,3+} _{б , в}
Вершины	$10T+2$	$4T+2$	$2T+2$
Лица	$20T$	$8T$	$4T$
Края	$30T$	$12T$	$6T$

Строительство

Геодезические многогранники строятся путем разделения граней более простых многогранников и последующего проецирования новых вершин на поверхность сферы. Геодезический многогранник имеет прямые ребра и плоские грани, приближающиеся к сфере, но его также можно сделать в виде сферического многогранника ( мозаика на сфере ) с истинно геодезическими изогнутыми краями на поверхности сферы и сферическими треугольными гранями.

Конвей	u ₃ I = (kt)I	(к)тИ	кти
Изображение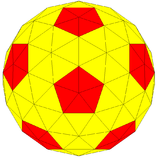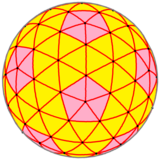
Форма	3-частотный разделенный икосаэдр	Кис усеченный икосаэдр	Геодезический многогранник (3,0)	Сферический многогранник

В этом случае {3,5+} _3,0 , с частотой $\nu =3$ и номер триангуляции $T=9$ , каждая из четырех версий многоугольника имеет 92 вершины (80, где соединяются шесть ребер, и 12, где соединяются пять), 270 ребер и 180 граней.

Связь с многогранниками Гольдберга

Геодезические многогранники являются двойственными многогранникам Гольдберга . Многогранники Гольдберга также связаны тем, что применение оператора kis (разделение граней на треугольники с центральной точкой) создает новые геодезические многогранники, а усечение вершин геодезического многогранника создает новый многогранник Гольдберга. Например, Goldberg G(2,1) kized становится {3,5+} _4,1 , а усечение становится G(6,3). Аналогично, усеченное {3,5+} _2,1 становится G(4,1), а кисед становится {3,5+} _6,3 .

Примеры

Класс I

Геодезические многогранники I класса
Частота	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	( м ,0)
Т	1	4	9	16	25	36	49	64	м ²
Лицо треугольник									...
икосаэдрический									более
Октаэдрический								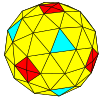	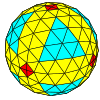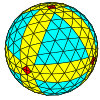более
Тетраэдрический									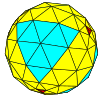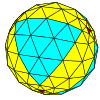более

Класс II

Геодезические многогранники II класса
Частота	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	( м , м )
Т	3	12	27	48	75	108	147	192	3 m ²
Лицо треугольник									...
икосаэдрический								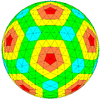	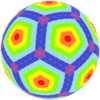более
Октаэдрический									более
Тетраэдрический									более

Класс III

Геодезические многогранники III класса
Частота	(2,1)	(3,1)	(3,2)	(4,1)	(4,2)	(4,3)	(5,1)	(5,2)	( м , н )
Т	7	13	19	21	28	37	31	39	м ²+ мин + н ²
Лицо треугольник									...
икосаэдрический									более
Октаэдрический									более
Тетраэдрический									более

Сферические модели

Магнуса Веннингера Книга «Сферические модели» исследует эти подразделения при построении моделей многогранников . Объяснив конструкцию этих моделей, он объяснил, как использует треугольные сетки для разметки узоров, причем треугольники окрашены или исключены из моделей. ^[6]

Пример модели
Художественная модель, созданная отцом Магнусом Веннингером , под названием Order in Chaos , представляющая собой киральное подмножество треугольников 16-частотной икосаэдрической геодезической сферы , {3,5+} _16,0	Виртуальная копия, показывающая икосаэдрической симметрии большие круги . Шестикратная вращательная симметрия иллюзорна и не существует на самом икосаэдре.	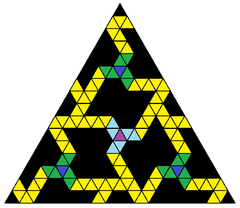Одиночный икосаэдрический треугольник с 16-частотным разделением.

См. также

Обозначение многогранника Конвея

Ссылки

^ Каспар, DLD; Клюг, А. (1962). «Физические принципы построения обычных вирусов». Холодный источник Харб. Симп. Квант. Биол . 27 : 1–24. дои : 10.1101/sqb.1962.027.001.005 . ПМИД 14019094 .
^ Коксетер, HSM (1971). «Вирусные макромолекулы и геодезические купола». В Батчере, Джей Си (ред.). Спектр математики . Издательство Оксфордского университета. стр. 98–107.
^ Андраде, Клебер; Герра, Сара; Дебют, Алексис (2014). «Симметрия на основе фуллеренов в пыльце Hibiscus rosa-sinensis» . ПЛОС ОДИН . 9 (7): e102123. Бибкод : 2014PLoSO...9j2123A . дои : 10.1371/journal.pone.0102123 . ПМК 4086983 . ПМИД 25003375 . См. также пыльцы ипомеи изображение .
^ «Примитивы сетки» , Справочное руководство Blender, версия 2.77 , получено 11 июня 2016 г.
^ «В чем разница между УФ-сферой и икосферой?» . Blender Обмен стеками .
^ Веннингер (1979) , стр. 150–159.

Библиография

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . С. 142–144, рис. 4-49, 50, 51 Кассеты из 12 сфер, 42 сфер, 92 сфер.
Пью, Энтони (1976). «Глава 6. Геодезические многогранники Р. Бакминстера Фуллера и родственные им многогранники». Многогранники: визуальный подход .
Веннингер, Магнус (1979). Сферические модели . Издательство Кембриджского университета . ISBN 978-0-521-29432-4 . МР 0552023 . Архивировано из оригинала 4 июля 2008 года. Перепечатано Dover (1999). ISBN 978-0-486-40921-4 .
Попко, Эдвард С. (2012). «Глава 8. Схемы подразделения, 8.1 Геодезические обозначения, 8.2 Число триангуляции 8.3 Частота и гармоники 8.4 Симметрия сетки 8.5 Класс I: альтернативы и броды 8.5.1 Определение главного треугольника 8.5.2 Краевые опорные точки». Разделенные сферы: геодезика и упорядоченное деление сферы .

[Caspar1962-1] Каспар, DLD; Клюг, А. (1962). «Физические принципы построения обычных вирусов». Холодный источник Харб. Симп. Квант. Биол . 27 : 1–24. дои : 10.1101/sqb.1962.027.001.005 . ПМИД 14019094 .

[2] Коксетер, HSM (1971). «Вирусные макромолекулы и геодезические купола». В Батчере, Джей Си (ред.). Спектр математики . Издательство Оксфордского университета. стр. 98–107.

[3] Андраде, Клебер; Герра, Сара; Дебют, Алексис (2014). «Симметрия на основе фуллеренов в пыльце Hibiscus rosa-sinensis» . ПЛОС ОДИН . 9 (7): e102123. Бибкод : 2014PLoSO...9j2123A . дои : 10.1371/journal.pone.0102123 . ПМК 4086983 . ПМИД 25003375 . См. также пыльцы ипомеи изображение .

[4] «Примитивы сетки» , Справочное руководство Blender, версия 2.77 , получено 11 июня 2016 г.

[5] «В чем разница между УФ-сферой и икосферой?» . Blender Обмен стеками .

[FOOTNOTEWenninger1979150–159-6] Веннингер (1979) , стр. 150–159.

[1]

[2]

[3]

[4]

[5]

[6]