Полиэдральная группа

Выбранные группы точек в трех измерениях

Инволюционная симметрия С ) , (* [ ] =	Циклическая симметрия C нв , (*nn) [н] =	Двугранная симметрия Д нх , (*n22) [п,2] =
Группа многогранников , [n,3], (*n32)
Тетраэдрическая симметрия Т д , (*332) [3,3] =	Октаэдрическая симметрия О х , (*432) [4,3] =	Икосаэдрическая симметрия I h , (*532) [5,3] =

В геометрии группа многогранников — любая из групп симметрии Платоновых тел .

Группы

Выделяют три группы многогранников:

• Тетраэдрическая группа 12-го порядка, вращательная группа симметрии правильного тетраэдра . Он изоморфен A ₄ .
  • Классы сопряжения T:
    • личность
    • 4 × поворот на 120°, порядок 3, по часовой стрелке
    • 4 × поворот на 120°, порядок 3, против часовой стрелки
    • 3 × поворот на 180°, порядок 2
• Октаэдрическая группа порядка 24, вращательная группа симметрии куба и правильный октаэдр . Он изоморфен S ₄ .
  • Классы сопряжения O:
    • личность
    • 6 × поворот на ±90° вокруг вершин, порядок 4
    • 8 × поворот на ±120° вокруг центров треугольников, порядок 3
    • 3 × поворот на 180° вокруг вершин, порядок 2
    • 6 × поворот на 180° вокруг середин ребер, порядок 2
• Группа икосаэдра порядка 60, группа вращательной симметрии правильного додекаэдра и правильного икосаэдра . Он изоморфен A ₅ .
  • Классы сопряженности I:
    • личность
    • 12 × поворот на ±72°, порядок 5
    • 12 × поворот на ±144°, порядок 5
    • 20 × поворот на ±120°, порядок 3
    • 15 × поворот на 180°, порядок 2

Эти симметрии удваиваются до 24, 48, 120 соответственно для полных отражающих групп. Симметрии отражения имеют соответственно 6, 9 и 15 зеркал. Октаэдрическую симметрию [4,3] можно рассматривать как объединение 6 зеркал тетраэдрической симметрии [3,3] и 3 зеркал двугранной симметрии Dih ₂ , [2,2]. Пиритоэдрическая симметрия — это еще одно удвоение тетраэдрической симметрии.

Классы сопряжений полной тетраэдрической симметрии T _d ≅ S ₄ :

• личность
• 8 × поворот на 120°
• 3 × поворот на 180°
• 6 × отражение в плоскости через две оси вращения
• 6 × поворот ротора на 90°

Классы сопряжения пиритоэдрической симметрии Th _{включают} классы T с двумя объединенными классами из 4 и каждый с инверсией:

• личность
• 8 × поворот на 120°
• 3 × поворот на 180°
• инверсия
• 8 × поворот ротора на 60°
• 3 × отражение в плоскости

Классы сопряжения полной октаэдрической Oh ₄ ≅ S ₂ × C _группы :

• инверсия
• 6 × поворот ротора на 90°
• 8 × поворот ротора на 60°
• 3 × отражение в плоскости, перпендикулярной оси 4-го порядка
• 6 × отражение в плоскости, перпендикулярной оси 2-го порядка

К классам сопряжений полной икосаэдрической симметрии I _h ≅ A ₅ × C ₂ относятся также каждый с инверсией:

• инверсия
• 12 × поворот ротора на 108°, порядок 10
• 12 × поворот ротора на 36°, порядок 10
• 20 × поворот ротора на 60°, порядок 6
• 15 × отражение, порядок 2

Киральные многогранные группы

Киральные полиэдральные группы

Имя ( Орб. )	Коксетер обозначение	Заказ	Абстрактный структура	Вращение очки # валентность	Диаграммы
					Ортогональный	Стереографический
Т (332)	[3,3] +	12	A 4	4 3 3 2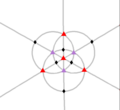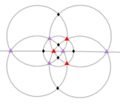
Т ч (3*2)	[4,3 + ]	24	А 4 × С 2	4 3 3 *2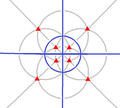
ТО (432)	[4,3] +	24	С 4	3 4 4 3 6 2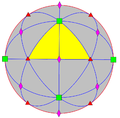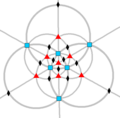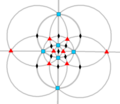
я (532)	[5,3] +	60	AА5	6 5 10 3 15 2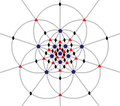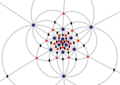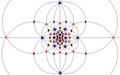

Полные многогранные группы

Полные многогранные группы

Вейль Обувь. ( Орб. )	Коксетер обозначение	Заказ	Абстрактный структура	Коксетер число (час)	Зеркала (м)	Зеркальные схемы
						Ортогональный	Стереографический
AА3 Т д (*332)	[3,3]	24	С 4	4	6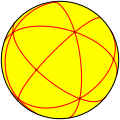
BБ3 Ой ​ (*432)	[4,3]	48	С 4 × С 2	8	3 >6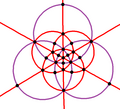
HH3 I h (*532)	[5,3]	120	А 5 х С 2	10	15

См. также

• Символ Витхоффа
• Список сферических групп симметрии

Ссылки

• Коксетер, Правильные многогранники HSM , 3-е изд. Нью-Йорк: Дувр, 1973. ( Многогранные группы . §3.5, стр. 46–47).

Внешние ссылки

• Вайсштейн, Эрик В. «Полиэдральная группа» . Математический мир .