Симметроэдр

В геометрии симметроэдр , высокой симметрии — многогранник содержащий выпуклые правильные многоугольники на осях симметрии с пробелами на выпуклой оболочке , заполненными неправильными многоугольниками.Название было придумано Крейгом С. Капланом и Джорджем У. Хартом . ^[1]

Тривиальными случаями являются Платоновы тела , Архимедовы тела со всеми правильными многоугольниками. Первый класс называется галстуком-бабочкой и содержит пары трапециевидных граней. У второго класса воздушные змеи. Другой класс называется симметроэдрами LCM .

Символическое обозначение

Каждый симметроэдр описывается символическим выражением G(l; m; n; α). G представляет группу симметрии (T,O,I). Значения l, m и n являются множителями; множитель m приведет к размещению правильного км-угольника на каждой k-кратной оси G. В обозначениях предполагается, что степени оси отсортированы в порядке убывания: 5,3,2 для I, 4,3 ,2 для O и 3,3,2 для T . Мы также допускаем два специальных значения для множителей: *, указывающее, что на заданных осях не должно быть размещено многоугольников, и 0, указывающее, что окончательное твердое тело должно иметь вершину (многоугольник с нулевыми сторонами) на осях. Мы требуем, чтобы одно или два из l, m и n были положительными целыми числами. Последний параметр α управляет относительными размерами невырожденных осей-угольников.

Обозначение многогранников Конвея — это еще один способ описания этих многогранников, начиная с правильной формы и применяя префиксные операторы. Обозначения не подразумевают, какие грани следует сделать регулярными за пределами однородных решений архимедовых тел .

Дуалы
Я(*;2;3;е)	Пиритоэдрический

1-генераторная точка

Эти симметроэдры создаются одной образующей точкой внутри фундаментальных доменов, отражающей симметрию на границах доменов. Ребра существуют перпендикулярно каждой границе треугольника, а правильные грани существуют в центре каждого из трех углов треугольника.

Симметроэдры можно расширить до евклидовых мозаик, используя симметрию правильной квадратной мозаики и двойственные пары треугольных и шестиугольных мозаик . Тайлинги, Q — квадратная симметрия p4m, H — гексагональная симметрия p6m.

решений существуют диаграммы Кокстера-Дынкина Для этих однородных многогранных , представляющие положение образующей точки внутри фундаментальной области. Каждый узел представляет собой одно из трёх зеркал на краю треугольника. Зеркальный узел окольцовывается, если точка-генератор активна, вне зеркала, и создает новые ребра между точкой и ее зеркальным изображением.

Домен	Края	Тетраэдрический (3 3 2)		Октаэдрический (4 3 2)		Икосаэдрический (5 3 2)		Треугольный (6 3 2)			Квадрат (4 4 2)
Домен	Края	Символ	Изображение	Символ	Изображение	Символ	Изображение	Символ	Изображение	Двойной	Символ	Изображение	Двойной
	1	Т(1;;;е) Т ,		С , О(1;;;е)		Я(1;;;е) Д ,		Н(1;;;е) Х ,			Q(1;;;е) Вопрос ,
	1	Т(;1;;е) дТ ,		О(;1;;е) Ой ,		Я(;1;;е) я ,		Ч(;1;;е) дХ ,			Q(;1;;e) дК ,
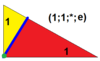	2	Т(1;1;*;е) в ,		О(1;1;*;е) до нашей эры ,		Я(1;1;*;е) АД ,		Н(1;1;*;е) АХ ,			Q(1;1;*;e) а-к ,
	3	Т(2;1;*;е) тТ ,		О(2;1;*;е) ТК ,		Я(2;1;*;е) тд ,		Н(2;1;*;е) тХ ,			Q(2;1;*;е) тQ ,
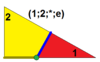	3	Т(1;2;*;е) дтт ,		О(1;2;*;е) к ,		Я(1;2;*;е) tIэто		Н(1;2;*;е) дтх ,			Q(1;2;*;е) dtQdtq
	4	Т(1;1;*;1) И ,		О(1;1;*;1) ЕС ,		Я(1;1;*;1) ЭД ,		Ч(1;1;*;1) эх ,			Q(1;1;*;1) эквалайзер ,
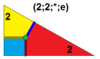	6	Т(2;2;*;е) БТ ,		О(2;2;*;е) до нашей эры ,		Я(2;2;*;е) бд ,		Н(2;2;*;е) бх ,			Q(2;2;*;е) бК ,

2-генераторные точки

Домен	Края	Тетраэдрический (3 3 2)		Октаэдрический (4 3 2)		Икосаэдрический (5 3 2)		Треугольный (6 3 2)			Квадрат (4 4 2)
Домен	Края	Символ	Изображение	Символ	Изображение	Символ	Изображение	Символ	Изображение	Двойной	Символ	Изображение	Двойной
	6	Т(1;2;*;[2]) к		О(1;2;*;[2]) atO		Я(1;2;*;[2]) у нас были		Ч(1;2;*;[2]) приΔ			Q(1;2;;[2]) Q(2;1;;[2]) atQ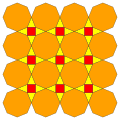
	6	Т(1;2;*;[2]) к		О(2;1;*;[2]) atC		Я(2;1;*;[2]) и т. д.		Ч(2;1;*;[2]) atH			Q(1;2;;[2]) Q(2;1;;[2]) atQ
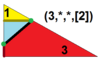	7	Т(3;;;[2]) Т(;3;;[2]) дКдТ		О(3;;;[2]) dKdC		Я(3;;;[2]) дКдД		Ч(3;;;[2]) дКдХ			Q(3;;;[2]) Q(;3;;[2]) dKQ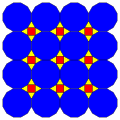
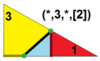	7	Т(3;;;[2]) Т(;3;;[2]) дКдТ		О(;3;;[2]) дКдо		Я(;3;;[2]) dKdI		Ч(;3;;[2]) dKdΔ			Q(3;;;[2]) Q(;3;;[2]) dKQ
	8	Т(2;3;;а) Т(3;2;;а) дМ ₀ Т		О(2;3;*;а) дМ ₀ дО		Я(2;3;*;а) дМ ₀ ди		Н(2;3;*;а) дМ ₀ dΔ			Q(2;3;;α) Q(3;2;;α) дМ ₀ Q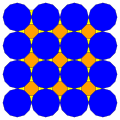
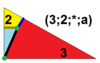	8	Т(2;3;;а) Т(3;2;;а) дМ ₀ Т		О(3;2;*;а) дМ ₀ постоянного тока		Я(3;2;*;а) дМ ₀ дД		Н(3;2;*;а) дМ ₀ дХ			Q(2;3;;α) Q(3;2;;α) дМ ₀ Q
	9	Т(2;4;;е) Т(4;2;;е) ТТТ		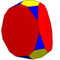О(2;4;*;е) ттО		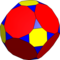Я(2;4;*;е) тт я		Н(2;4;*;е) ТТД			Q(4;2;;e) Q(2;4;;e) ttQ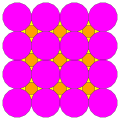
	9	Т(2;4;;е) Т(4;2;;е) ТТТ		О(4;2;*;е) ТТК		Я(4;2;*;е) ТТД		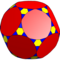Н(4;2;*;е) ТТХ			Q(4;2;;e) Q(2;4;;e) ttQ
	7	Т(2;1;;1) Т(1;2;;1) дМ 3Т		О(1;2;*;1) дМ ₃ О		Я(1;2;*;1) dM₃dM3I		Ч(1;2;*;1) дМ ₃ Δ			Q(2;1;;1) Q(1;2;;1) дМ ₃ дQ
	7	Т(2;1;;1) Т(1;2;;1) дМ 3Т		О(2;1;*;1) дМ ₃ С		Я(2;1;*;1) дМ ₃ Д		Ч(2;1;*;1) дМ ₃ Ч			Q(2;1;;1) Q(1;2;;1) дМ ₃ дQ
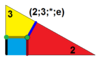	9	Т(2;3;;е) Т(3;2;;е) дм 3Т		О(2;3;*;е) дм ₃ С		Я(2;3;*;е) дм ₃ Д		Н(2;3;*;е) дм ₃ Ч			Q(2;3;;e) Q(3;2;;e) дм ₃ Q
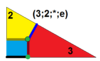	9	Т(2;3;;е) Т(3;2;;е) дм 3Т		О(3;2;*;е) дм ₃ О		Я(3;2;*;е) дм ₃ я		Н(3;2;*;е) дм ₃ Δ			Q(2;3;;e) Q(3;2;;e) дм ₃ Q
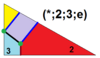	10	Т(2;;3;е) Т(;2;3;е) dXdT 3.4.6.6		О(*;2;3;е) dXdO		Я(*;2;3;е) dXdI		Ч(*;2;3;е) dXdΔ			Q(2;;3;e) Q(;2;3;е) dXdQ
	10	Т(2;;3;е) Т(;2;3;е) dXdT 3.4.6.6		О(2;*;3;е) dXdC 3.4.6.8		Я(2;*;3;е) dXdD 3.4.6.10		Н(2;*;3;е) dXdH 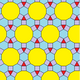3.4.6.12			Q(2;;3;e) Q(;2;3;е) dXdQ

3-генераторные точки

Домен	Края	Тетраэдрический (3 3 2)		Октаэдрический (4 3 2)		Икосаэдрический (5 3 2)		Треугольный (6 3 2)			Квадрат (4 4 2)
Домен	Края	Символ	Изображение	Символ	Изображение	Символ	Изображение	Символ	Изображение	Двойной	Символ	Изображение	Двойной
	6	Т(2;0;*;[1])		О(0;2;*;[1]) дл ₀ дО		Я(0;2;*;[1]) дл ₀ ди		Ч(0;2;*;[1]) дл ₀ Ч			Q(2;0;;[1]) Q(0;2;;[1]) дл ₀ дQ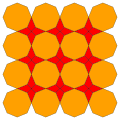
	6	Т(2;0;*;[1])		О(2;0;*;[1]) дл ₀ постоянного тока		Я(2;0;*;[1]) дл ₀ дД		Ч(2;0;*;[1]) дл ₀ Д			Q(2;0;;[1]) Q(0;2;;[1]) дл ₀ дQ
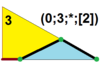	7	Т(3;0;*;[2])		О(0;3;*;[2]) ДЛДО		Я(0;3;*;[2]) dLdI		Ч(0;3;*;[2]) dLH			Q(2;0;;[1]) Q(0;2;;[2]) дллк
	7	Т(3;0;*;[2])		О(3;0;*;[2]) dLdC		Я(3;0;*;[2]) dLDD		Ч(3;0;*;[2]) dLΔ			Q(2;0;;[1]) Q(0;2;;[2]) дллк
	12	Т(2;2;*;а) утра		О(2;2;*;а) AMC		Я(2;2;*;а) AMD		Н(2;2;*;а) утра			Q(2;2;*;а) amQ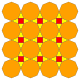

См. также

Ссылки

^ Симметроэдры: Многогранники из симметричного размещения правильных многоугольников

Внешние ссылки

Симметроэдры — это RobertLovesPi.net.
Antiprism Бесплатное программное обеспечение, включающее Symmetro для создания и просмотра этих многогранников в нотации Каплана-Харта.

[1] Симметроэдры: Многогранники из симметричного размещения правильных многоугольников

[1]