3-4-6-12 плитка

3-4-6-12 плитка

Тип	2-равномерная мозаика
Конфигурация вершин	3.4.6.4 и 4.6.12
Симметрия	п6м, [6,3], (*632)
Симметрия вращения	р6, [6,3] ⁺, (632)
Характеристики	2-однородный, 4- изоэдрический , 4- изотоксальный

В геометрии евклидовой плоскости замощение 3-4-6-12 — это одно из 20 2-однородных замощений евклидовой плоскости правильными многоугольниками , содержащее правильные треугольники , квадраты , шестиугольники и додекагоны , расположенные в двух конфигурациях вершин : 3.4. 6.4 и 4.6.12. ^[1]^[2]^[3]^[4]

Он имеет гексагональную симметрию , p6m, [6,3], (*632). также называют его полурегулярным замощением Некоторые авторы .

Геометрия

Две его конфигурации вершин являются общими для двух 1-однородных мозаик:

ромбитригексагональная мозаика	усеченная тригексагональная мозаика
3.4.6.4	4.6.12

Его можно рассматривать как разновидность уменьшенной ромбитригексагональной мозаики , в которой додекагоны заменяют периодические наборы шестиугольников и окружающие их квадраты и треугольники. Это похоже на тело Джонсона , уменьшенный ромбикосидодекаэдр , который представляет собой ромбикосидодекаэдр с удаленными гранями, что приводит к появлению новых десятиугольных граней. Двойной вариант этого варианта показан справа (дельтовидные шестиугольные вставки).

Связанные k -однородные мозаики правильных многоугольников

Шестиугольники можно разрезать на 6 треугольников, а додекагоны — на треугольники, шестиугольники и квадраты.

Разрезанные полигоны
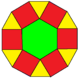Шестиугольник	Додекагон (каждый имеет 2 направления)


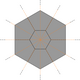Двойные процессы (двойные «вставки»)

3-однородные мозаики
48	26	18 (2-униформа)
[3 ⁶; 3 ².4.3.4; 3 ².4.12]	[3.4 ².6; (3.4.6.4) ²]	[3 ⁶; 3 ².4.3.4]
V[3 ⁶; 3 ².4.3.4; 3 ².4.12]	V[3.4 ².6; (3.4.6.4) ²]	V[3 ⁶; 3 ².4.3.4]
3-униформные дуальные

Круговая упаковка

Эту 2-однородную мозаику можно использовать как упаковку кругов . Голубые круги соприкасаются с тремя другими кругами (2 голубыми, 1 розовый), что соответствует планигону V4.6.12, а розовые круги соприкасаются с четырьмя другими кругами (1 голубой, 2 розовых), что соответствует V3.4.6. 4 планигона. Он гомеоморфен операции ambo на мозаике: голубые и розовые многоугольники с промежутками соответствуют голубым и розовым кругам (многоугольники с мини-вершинной конфигурацией; одномерные двойники соответствующим плоскостям). Оба изображения совпадают.


С [3.4.6.12]	а[3.4.6.12]

Двойная черепица

Двойная мозаика имеет прямоугольные треугольные и воздушные грани, определяемые конфигурациями граней : V3.4.6.4 и V4.6.12, и ее можно увидеть в сочетании дельтовидной тригексагональной мозаики и кисромбилловой мозаики .

Двойная черепица	Версия 3.4.6.4 Версия 4.6.12	Дельтоидная тригексагональная мозаика	Кисромбилльная плитка

Примечания

^ Кричлоу, стр. 62–67.
^ Грюнбаум и Шепард 1986, стр. 65–67.
^ В поисках полурегулярных мозаик № 4
^ Чави (1989)

Ссылки

Кейт Кричлоу, Порядок в космосе: справочник по дизайну , 1970, стр. 62–67.
Гика, М. Геометрия искусства и жизни , (1946), 2-е издание, Нью-Йорк: Дувр, 1977. Демирегулярная плитка № 15.
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . стр. 35–43
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . У. Х. Фриман. ISBN 0-7167-1193-1 . п. 65
Справочник по дизайну сакральной геометрии: Универсальные размерные модели , Брюс Роулз, 1997. стр. 36–37 [1]

Внешние ссылки

Чави, Д. (1989). «Замощения правильными многоугольниками - II: Каталог мозаик» . Компьютеры и математика с приложениями . 17 : 147–165. дои : 10.1016/0898-1221(89)90156-9 .
Датч, Стив. «Единые плитки» . Архивировано из оригинала 9 сентября 2006 г. Проверено 9 сентября 2006 г.
Вайсштейн, Эрик В. «Демирегулярная мозаика» . Математический мир .
В поисках полурегулярных мозаик , Хельмер Аслаксен
n -равномерные мозаики Брайан Галебах, 2-однородные мозаики 1 из 20

[1] Кричлоу, стр. 62–67.

[2] Грюнбаум и Шепард 1986, стр. 65–67.

[3] В поисках полурегулярных мозаик № 4

[4] Чави (1989)

[1]

[2]

[3]

[4]