Трехгексагональная плитка
| Трехгексагональная плитка | |
|---|---|
 | |
| Тип | Полурегулярная черепица |
| Конфигурация вершин |  (3.6) 2 |
| Символ Шлефли | г{6,3} или ч 2 {6,3} |
| Символ Витхоффа | 2 | 6 3 3 3 | 3 |
| Диаграмма Кокстера |       =  |
| Симметрия | p6m , [6,3], (*632) |
| Симметрия вращения | р6 , [6,3] + , (632) р3 , [3 [3] ] + , (333) |
| Аббревиатура Бауэрса | Что |
| Двойной | Ромбическая плитка |
| Характеристики | Вершинно-транзитивный. Реберно-транзитивный. |
В геометрии тригексагональное замощение — одно из 11 однородных замощений евклидовой плоскости правильными многоугольниками . [1] Он состоит из равносторонних треугольников и правильных шестиугольников , расположенных так, что каждый шестиугольник окружен треугольниками и наоборот. Название происходит от того факта, что оно сочетает в себе правильную шестиугольную мозаику и правильную треугольную мозаику . чередуются два шестиугольника и два треугольника Вокруг каждой вершины , а ее края образуют бесконечное множество линий . Его двойником является ромбовидная мозаика . [2]
Эта закономерность и ее место в классификации однородных мозаик уже были известны Иоганну Кеплеру в его книге «Harmonices Mundi» 1619 года . [3] Узор издавна использовался в японском плетении , где он называется кагоме . Японский термин, обозначающий эту структуру, был использован в физике, где она называется решеткой кагоме . Он встречается также в кристаллических структурах некоторых минералов. Конвей называет это гексадельтиллем , комбинируя альтернативные элементы шестиугольной мозаики (гекстиль) и треугольной мозаики (дельтиль). [4]
Кагоме
[ редактировать ]
Кагоме ( яп . 籠目 ) — традиционный японский узор из бамбука; его название состоит из слов каго , что означает «корзина», и ме , что означает «глаз (глаза)», что относится к узору отверстий в плетеной корзине.
Узор кагоме распространен в бамбуковом ткачестве в Восточной Азии. В 2022 году археологи обнаружили останки бамбукового плетения на руинах Донгсунба в Чунцине, Китай, 200 г. до н.э. Спустя 2200 лет модель кагоме все еще ясна. [5] [6]
Инуитские снегоступы Таглук
Выкройка Кагоме в деталях
Это плетеное расположение реек, состоящее из переплетенных треугольников, так что каждая точка пересечения двух реек имеет четыре соседние точки, образуя узор трехгексагональной плитки. Процесс ткачества придает Кагоме хиральную симметрию группы обоев , p6 (632).
Решетка Кагоме
[ редактировать ]Термин «решетка кагоме» был придуман японским физиком Коди Хусими и впервые появился в статье 1951 года его помощника Ичиро Сёдзи. [7] Решетка кагоме в этом смысле состоит из вершин и ребер тригексагональной мозаики.Несмотря на название, эти точки пересечения не образуют математической решетки .
Родственная трехмерная структура, образованная вершинами и краями четвертькубических сот , заполняющих пространство правильными тетраэдрами и усеченными тетраэдрами , была названа решеткой гиперкагоме . [8] Он представлен вершинами и ребрами четвертькубических сот , заполняющих пространство правильными тетраэдрами и усеченными тетраэдрами . Он содержит четыре набора параллельных плоскостей точек и линий, каждая плоскость представляет собой двумерную решетку кагоме. Второе выражение в трех измерениях имеет параллельные слои двумерных решеток и называется решеткой ромбического кагоме . [8] Трехшестиугольные призматические соты представляют собой его края и вершины.
Некоторые минералы , а именно ярозиты и гербертсмитит двумерные слои или трехмерную решетчатую структуру кагоме , содержат в своей кристаллической структуре . Эти минералы демонстрируют новые физические свойства, связанные с геометрически нарушенным магнетизмом . Например, спиновое расположение магнитных ионов в Co 3 V 2 O 8 основано на решетке кагоме, которая демонстрирует удивительное магнитное поведение при низких температурах. [9] квантовые магниты, реализованные на металлах Кагоме, демонстрируют множество неожиданных электронных и магнитных явлений. Было обнаружено, что [10] [11] [12] [13] Также предполагается, что поведение SYK можно наблюдать в двумерной решетке кагоме с примесями. [14]
Этот термин сегодня широко используется в научной литературе, особенно теоретиками, изучающими магнитные свойства теоретической решетки кагоме.
См. также: Гербы Кагоме .
Симметрия
[ редактировать ]
Тригексагональная мозаика имеет символ Шлефли r{6,3} или диаграмму Коксетера , , символизируя тот факт, что это выпрямленная шестиугольная мозаика , {6,3}. Его симметрию можно описать группой обоев p6mm, (*632), [15] и мозаика может быть получена как конструкция Витхоффа внутри отражающих фундаментальных областей этой группы . Тригексагональная мозаика представляет собой квазиправильную мозаику , состоящую из чередующихся двух типов многоугольников, с конфигурацией вершин (3.6) 2 . Это также однородная мозаика , одна из восьми, полученных на основе правильной шестиугольной мозаики.
Равномерные раскраски
[ редактировать ]имеет две различные однородные раскраски Тригексагональная мозаика . Именование цветов по индексам на 4-х гранях вокруг вершины (3.6.3.6): 1212, 1232. [1] Второй называется кантической шестиугольной мозаикой h 2 {6,3} с двумя цветами треугольников, существующей в p3m1 симметрии (*333).
| Симметрия | п6м, (*632) | п3м, (*333) |
|---|---|---|
| Раскраска |  |  |
| фундаментальный домен |  |  |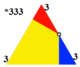
| Витхофф | 2 | 6 3 | 3 3 | 3 |
| Коксетер | | = |
| Шлефли | г{6,3} | г{3 [3] } = час 2 {6,3} |
Упаковка круга
[ редактировать ]Тригексагональную мозаику можно использовать в качестве упаковки кругов , размещая круги одинакового диаметра в центре каждой точки. [16] Каждый круг соприкасается с четырьмя другими кругами упаковки ( число поцелуя ).
Топологически эквивалентные мозаики
[ редактировать ]Тригексагональная мозаика может быть геометрически искажена в топологически эквивалентную мозаику более низкой симметрии. [1] В этих вариантах укладки края не обязательно совпадают, образуя прямые линии.
| p3m1, (*333) | п3, (333) | п31м, (3*3) | см, (2*22) | |||
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
Связанные квазирегулярные мозаики
[ редактировать ]Тригексагональная мозаика существует в последовательности симметрий квазирегулярных мозаик с конфигурациями вершин (3. n ) 2 , переходя от мозаик сферы к евклидовой плоскости и к гиперболической плоскости. При симметрии орбифолдной записи * n 32 все эти мозаики не построены внутри фундаментальной области симметрии с образующими точками в прямоугольном углу области. [17] [18]
| * n 32 орбифолдных симметрии квазирегулярных мозаик : (3. n ) 2 |
|---|
Родственные регулярные сложные апейрогоны
[ редактировать ]Есть два правильных комплексных апейрогона , разделяющих вершины тригексагональной мозаики. Правильные комплексные апейрогоны имеют вершины и ребра, причем ребра могут содержать 2 и более вершин. Правильные апейрогоны p { q } r ограничены следующим образом: 1/ p + 2/ q + 1/ r = 1. Ребра имеют p вершин, расположенных как правильный многоугольник , а фигуры вершин являются r -угольными. [19]
Первый состоит из треугольных ребер, по два вокруг каждой вершины, второй имеет шестиугольные ребра, по два вокруг каждой вершины.
 |  |
3{12}2 или   | 6{6}2 или  |
|---|
См. также
[ редактировать ]
- Порог перколяции
- Герб Кагоме
- Звезда Давида
- Трехгексагональные призматические соты
- Циклоусеченные симплектические соты
- Список однородных мозаик
Ссылки
[ редактировать ]- ^ Jump up to: Перейти обратно: а б с Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . У. Х. Фриман. ISBN 978-0-7167-1193-3 . См., в частности, теорему 2.1.3, с. 59 (классификация однородных замощений); Рисунок 2.1.5, с.63 (иллюстрация этого разбиения), Теорема 2.9.1, с. 103 (классификация цветных замощений), рис. 2.9.2, с. 105 (иллюстрация цветных мозаик), рисунок 2.5.3(d), с. 83 (топологически эквивалентное замощение звездой) и упражнение 4.1.3, с. 171 (топологическая эквивалентность тригексагональных и двухтреугольных мозаик).
- ^ Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 38. ISBN 0-486-23729-Х .
- ^ Эйтон, Э.Дж.; Дункан, Алистер Мэтисон; Филд, Джудит Вероника , ред. (1997). Гармония мира Иоганна Кеплера . Мемуары Американского философского общества. Том. 209. Американское философское общество. стр. 104–105. ISBN 978-0-87169-209-2 . .
- ^ Конвей, Джон Х .; Бургель, Хайди; Гудман-Штраус, Хаим (2008). «Глава 21: Именование архимедовых и каталанских многогранников и мозаик; мозаика евклидовой плоскости». Симметрии вещей . Уэлсли, Массачусетс: AK Peters, Ltd. 288. ИСБН 978-1-56881-220-5 . МР 2410150 .
- ^ Центральное телевидение Китая, новостной канал CCTV-13 (25 марта 2022 г.). «[Комната новостей] Бамбуковые ткацкие изделия культуры Ба впервые появились в Чунцине около 2200 лет назад» . tv.cctv.com . Проверено 20 марта 2023 г.
{{cite web}}: CS1 maint: числовые имена: список авторов ( ссылка ) - ^ Инь, Цзя-Синь (март 2023 г.). «Исследование до сих пор неизвестных квантовых фаз в кристаллах кагоме». Физика (物理) . 52 (3): 157–165. дои : 10.7693/wl20230301 .
- ^ Меката, Мамору (февраль 2003 г.). «Кагоме: История плетеной решетки» . Физика сегодня . 56 (2): 12–13. Бибкод : 2003ФТ....56б..12М . дои : 10.1063/1.1564329 .
- ^ Jump up to: Перейти обратно: а б Лоулер, Майкл Дж.; Ки, Хэ Ён; Ким, Ён Бэк; Вишванат, Ашвин (2008). «Топологическая спиновая жидкость на решетке гиперкагома Na 4 Ir 3 O 8 ». Письма о физических отзывах . 100 (22): 227201. arXiv : 0705.0990 . Бибкод : 2008PhRvL.100v7201L . дои : 10.1103/physrevlett.100.227201 . ПМИД 18643453 . S2CID 31984687 .
- ^ Йен, Ф.; Чаудхури, РП; Галстян Э.; Лоренц, Б.; Ван, YQ; Вс, ГГ; Чу, CW (2008). «Магнитные фазовые диаграммы лестничного соединения Кагоме Co 3 V 2 O 8 ». Физика Б: Конденсированное вещество . 403 (5–9): 1487–1489. arXiv : 0710.1009 . Бибкод : 2008PhyB..403.1487Y . дои : 10.1016/j.physb.2007.10.334 . S2CID 14958188 .
- ^ «Квантовый магнит с топологическим поворотом» . Открытие: исследования в Принстоне . 22 февраля 2019 г. Проверено 26 апреля 2020 г.
- ^ Инь, Цзя-Синь; Чжан, Сунтянь С.; Ли, Ханг; Цзян, Кун; Чанг, Гоцин; Чжан, Бинцзин; Лиан, Бяо; Сян, Ченг; Белопольский (2018). «Гигантская и анизотропная спин-орбитальная перестраиваемость многих тел в сильно коррелированном магните кагоме» . Природа . 562 (7725): 91–95. arXiv : 1810.00218 . Бибкод : 2018Natur.562...91Y . дои : 10.1038/s41586-018-0502-7 . ПМИД 30209398 . S2CID 205570556 .
- ^ Инь, Цзя-Синь; Чжан, Сунтянь С.; Чанг, Гоцин; Ван, Ци; Циркин Степан С.; Гугучия, Зураб; Лиан, Бяо; Чжоу, Хуэйбинь; Цзян, Кун; Белопольский, Илья; Шумия, Нана (2019). «Отрицательный плоский зонный магнетизм в коррелированном магните кагоме со спин-орбитальной связью» . Физика природы . 15 (5): 443–8. arXiv : 1901.04822 . Бибкод : 2019NatPh..15..443Y . дои : 10.1038/s41567-019-0426-7 . S2CID 119363372 .
- ^ Язьев, Олег В. (2019). «Перевернутый магнит» . Физика природы . 15 (5): 424–5. Бибкод : 2019NatPh..15..424Y . дои : 10.1038/s41567-019-0451-6 . S2CID 128299874 .
- ^ Вэй, Ченань; Седракян, Тигран (29 января 2021 г.). «Оптическая решетчатая платформа для модели Сачдева-Е-Китаева». Физ. Преподобный А. 103 (1): 013323. arXiv : 2005.07640 . Бибкод : 2021PhRvA.103a3323W . дои : 10.1103/PhysRevA.103.013323 . S2CID 234363891 .
- ^ Штойрер, Вальтер; Делуди, София (2009). Кристаллография квазикристаллов: понятия, методы и структуры . Серия Спрингера по материаловедению. Том. 126. Спрингер. п. 20. ISBN 978-3-642-01899-2 .
- ^ Кричлоу, Кейт (2000) [1969]. «образец Г». Порядок в космосе: справочник по дизайну . Темза и Гудзон. стр. 74–75. ISBN 978-0-500-34033-2 .
- ^ Коксетер, HSM (1973). «V. Калейдоскоп, §5.7 Конструкция Витгофа». Правильные многогранники (3-е изд.). Дувр. ISBN 0-486-61480-8 .
- ^ Хьюсон, Дэниел Х. «Мутации двумерной симметрии». CiteSeerX 10.1.1.30.8536 .
- ^ Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. стр. 111–2, 136. ISBN. 978-0-521-39490-1 .
Дальнейшее чтение
[ редактировать ]- Сеймур, Дейл; Бриттон, Джилл (1989). Введение в тесселяции . стр. 50–56. ISBN 978-0-86651-461-3 .
