В прототип

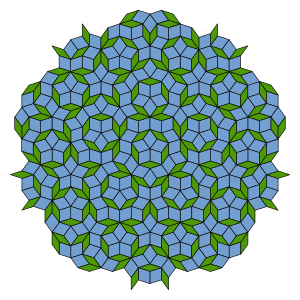
В математике прототип — это одна из форм плитки в мозаике . ^[1]

Определение

Мозаика плоскости или любого другого пространства представляет собой покрытие пространства замкнутыми формами, называемыми плитками, которые имеют непересекающуюся внутреннюю часть . Некоторые плитки могут совпадать с одним или несколькими другими. Если $S$ — набор плиток в мозаике, набор $фигур R$ называется набором прототипов, если никакие две фигуры в $R$ не конгруэнтны друг другу, и каждая плитка в $S$ конгруэнтна одной из фигур в $R$ . ^[2]

Для мозаики можно выбрать множество различных наборов прототипов: перемещение или поворот любого из прототипов создает другой действительный набор прототипов. Однако каждый набор прототайлов имеет одинаковую мощность , поэтому количество прототайлов четко определено. Тесселяция называется моноэдральной , если она имеет ровно один прототип.

Апериодичность

Набор прототайлов называется апериодическим, если каждое замощение этими прототайлами является апериодическим . В марте 2023 года четыре исследователя, Хаим Гудман-Штраус , Дэвид Смит , Джозеф Сэмюэл Майерс и Крейг С. Каплан, объявили об открытии апериодического моноэдрального прототиля (монотила) и доказательстве того, что плитка, открытая Дэвидом Смитом, является апериодическим монотилем. т.е. решение давней открытой проблемы Эйнштейна . ^[3]^[4]

В более высоких измерениях проблема была решена ранее: плитка Шмитта-Конвея-Данцера является прототипом моноэдральной апериодической мозаики трехмерного евклидова пространства и не может периодически замостить пространство.

Ссылки

^ Седерберг, Джудит Н. (2001), Курс современной геометрии , Тексты для студентов по математике (2-е изд.), Springer-Verlag, стр. 174, ISBN 978-0-387-98972-3 .
^ Каплан, Крейг С. (2009), Вводная теория тайлинга для компьютерной графики , Обобщающие лекции по компьютерной графике и анимации, Morgan & Claypool Publishers, стр. 7, ISBN 978-1-60845-017-6 .
^ Робертс, Шивон (28 марта 2023 г.). «Неуловимый «Эйнштейн» решает давнюю математическую задачу» . Нью-Йорк Таймс . ISSN 0362-4331 . Проверено 2 июня 2023 г.
^ Смит, Дэвид; Джозеф Сэмюэл Майерс; Каплан, Крейг С.; Гудман-Штраус, Хаим (2023). «Апериодический монотиль». arXiv : 2303.10798 [ math.CO ].

[1] Седерберг, Джудит Н. (2001), Курс современной геометрии , Тексты для студентов по математике (2-е изд.), Springer-Verlag, стр. 174, ISBN 978-0-387-98972-3 .

[2] Каплан, Крейг С. (2009), Вводная теория тайлинга для компьютерной графики , Обобщающие лекции по компьютерной графике и анимации, Morgan & Claypool Publishers, стр. 7, ISBN 978-1-60845-017-6 .

[3] Робертс, Шивон (28 марта 2023 г.). «Неуловимый «Эйнштейн» решает давнюю математическую задачу» . Нью-Йорк Таймс . ISSN 0362-4331 . Проверено 2 июня 2023 г.

[4] Смит, Дэвид; Джозеф Сэмюэл Майерс; Каплан, Крейг С.; Гудман-Штраус, Хаим (2023). «Апериодический монотиль». arXiv : 2303.10798 [ math.CO ].

[1]

[2]

[3]

[4]