Усеченная апейрогональная мозаика порядка 4

Усеченная апейрогональная мозаика порядка 4
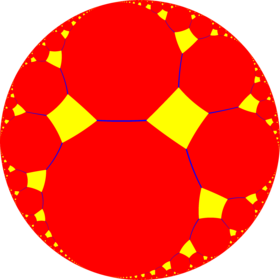Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая равномерная мозаика
Конфигурация вершин	4.∞.∞
Символ Шлефли	т{∞,4} tr{∞,∞} или $t{\begin{Bmatrix}\infty \\\infty \end{Bmatrix}}$
Символ Витхоффа	2 4 \| ∞ 2 ∞ ∞ \|
Диаграмма Кокстера	или
Группа симметрии	[∞,4], (∞42) [∞,∞], (∞∞2)
Двойной	Квадратная мозаика тетракиса бесконечного порядка
Характеристики	Вершинно-транзитивный

В геометрии усеченное апейрогональное замощение четвертого порядка представляет собой однородное замощение гиперболической плоскости . Он имеет символ Шлефли t{∞,4}.

Равномерные раскраски

Раскраска полусимметрии — tr{∞,∞}, имеет два типа апейрогонов, показанных здесь красным и желтым. Если апейрогональная кривизна слишком велика, она не сходится к одной идеальной точке, как на изображении справа (красные апейрогоны внизу). Диаграмма Коксетера показана пунктирными линиями для этих расходящихся ультрапараллельных зеркал .

(по центру вершины)	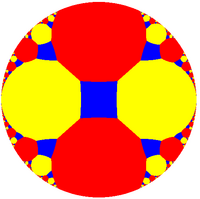(Квадрат по центру)

Симметрия

Из-за симметрии [∞, ∞] существует 15 малых индексных подгрупп путем удаления и чередования зеркал. Зеркала можно удалить, если все его порядки ветвей четные, и это сокращает соседние порядки ветвей пополам. Удаление двух зеркал оставляет точку вращения половинного порядка, где встречаются удаленные зеркала. В этих изображениях фундаментальные области попеременно окрашены в черный и белый цвета, а на границах между цветами существуют зеркала. Симметрию можно удвоить до симметрии ∞42 , добавив зеркало, делящее пополам фундаментальную область. Индекс подгруппы -8 группа, [1 ⁺,∞,1 ⁺,∞,1 ⁺] (∞∞∞∞) — коммутатор группы [∞,∞].

Малые индексные подгруппы группы [∞,∞] (*∞∞2)
Индекс	1	2			4
Диаграмма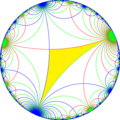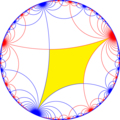
Коксетер	[∞,∞] =	[1 ⁺,∞,∞] =	[∞,∞,1 ⁺] =	[∞,1 ⁺,∞] =	[1 ⁺,∞,∞,1 ⁺] =	[∞ ⁺,∞ ⁺]
Орбифолд	*∞∞2	*∞∞∞		*∞2∞2	*∞∞∞∞	∞∞×
Полупрямые подгруппы
Диаграмма
Коксетер		[∞,∞ ⁺]	[∞ ⁺,∞]	[(∞,∞,2 ⁺)]	[∞,1 ⁺,∞,1 ⁺] = = = =	[1 ⁺,∞,1 ⁺,∞] = = = =
Орбифолд		∞*∞		2*∞∞	∞*∞∞
Прямые подгруппы
Индекс	2	4			8
Диаграмма
Коксетер	[∞,∞] ⁺ =	[∞,∞ ⁺] ⁺ =	[∞ ⁺,∞] ⁺ =	[∞,1 ⁺,∞] ⁺ =	[∞ ⁺,∞ ⁺] ⁺ = [1 ⁺,∞,1 ⁺,∞,1 ⁺] = = =
Орбифолд	∞∞2	∞∞∞		∞2∞2	∞∞∞∞
Радикальные подгруппы
Индекс		∞		∞
Диаграмма
Коксетер		[∞,∞*]	[∞*,∞]	[∞,∞*] ⁺	[∞*,∞] ⁺
Орбифолд		*∞ ^∞		∞ ^∞

Связанные многогранники и мозаика

* n 42 мутация симметрии усеченных мозаик: 4,2 n .2 n v т и
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis figures
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Паракомпактные равномерные разбиения семейства [∞,4] v т и


{∞,4}	t{∞,4}	r{∞,4}	2t{∞,4}=t{4,∞}	2r{∞,4}={4,∞}	rr{∞,4}	tr{∞,4}
Dual figures


V∞⁴	V4.∞.∞	V(4.∞)²	V8.8.∞	V4^∞	V4³.∞	V4.8.∞
Alternations
[1⁺,∞,4] (*44∞)	[∞⁺,4] (∞*2)	[∞,1⁺,4] (*2∞2∞)	[∞,4⁺] (4*∞)	[∞,4,1⁺] (*∞∞2)	[(∞,4,2⁺)] (2*2∞)	[∞,4]⁺ (∞42)
=				=
h{∞,4}	s{∞,4}	hr{∞,4}	s{4,∞}	h{4,∞}	hrr{∞,4}	s{∞,4}

Alternation duals


V(∞.4)⁴	V3.(3.∞)²	V(4.∞.4)²	V3.∞.(3.4)²	V∞^∞	V∞.4⁴	V3.3.4.3.∞

Паракомпактные равномерные разбиения семейства [∞,∞] v т и
= =	= =	= =	= =	= =	=	=

{∞,∞}	t{∞,∞}	r{∞,∞}	2t{∞,∞}=t{∞,∞}	2r{∞,∞}={∞,∞}	rr{∞,∞}	tr{∞,∞}
Dual tilings


V∞^∞	V∞.∞.∞	V(∞.∞)²	V∞.∞.∞	V∞^∞	V4.∞.4.∞	V4.4.∞
Alternations
[1⁺,∞,∞] (*∞∞2)	[∞⁺,∞] (∞*∞)	[∞,1⁺,∞] (*∞∞∞∞)	[∞,∞⁺] (∞*∞)	[∞,∞,1⁺] (*∞∞2)	[(∞,∞,2⁺)] (2*∞∞)	[∞,∞]⁺ (2∞∞)


h{∞,∞}	s{∞,∞}	hr{∞,∞}	s{∞,∞}	h₂{∞,∞}	hrr{∞,∞}	sr{∞,∞}
Alternation duals


V(∞.∞)^∞	V(3.∞)³	V(∞.4)⁴	V(3.∞)³	V∞^∞	V(4.∞.4)²	V3.3.∞.3.∞

См. также

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Внешние ссылки