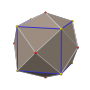
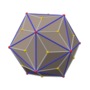
Тетракис шестигранник

Тетракис шестигранник
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Каталонский солид
Диаграмма Кокстера
Обозначение Конвея	кС
Тип лица	Версия 4.6.6 равнобедренный треугольник
Лица	24
Края	36
Вершины	14
Вершины по типу	6{4}+8{6}
Группа симметрии	О _h , B ₃ , [4,3], (*432)
Группа ротации	О, [4,3] ⁺, (432)
Двугранный угол	143°07′48″ арккос(- ⁠ 4 / 5 ⁠ )
Характеристики	выпуклый, гране-переходный
Усеченный октаэдр ( двойной многогранник )	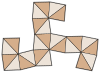Сеть

Двойное соединение усеченного октаэдра и тетракис-гексаэдра. Гравюра слева взята из Perspectiva Corporum Regularium (1568) Венцеля Ямнитцера .

Модель штампа и кристалла

Рисунок и кристаллическая модель варианта с тетраэдрической симметрией, называемого гексакис-тетраэдром. ^[1]

В геометрии тетракис - гексаэдр (также известный как тетрагексаэдр , гексетраэдр , тетракис-куб и кискуб) ^[2]) — каталонское твердое тело . Его двойником является усеченный октаэдр , архимедово тело .

Его можно назвать дисдиакиса или гексакис-тетраэдром как двойником всеусеченного тетраэдра гексаэдром и как барицентрическое подразделение тетраэдра. ^[3]

Декартовы координаты

Декартовы координаты 14 вершин тетракис-шестиэдра с центром в начале координат - это точки ${\bigl (}{\pm {\tfrac {3}{2}}},0,0{\bigr )},\ {\bigl (}0,\pm {\tfrac {3}{2}},0{\bigr )},\ {\bigl (}0,0,\pm {\tfrac {3}{2}}{\bigr )},\ {\bigl (}{\pm 1},\pm 1,\pm 1{\bigr )}.$

Длина более коротких ребер этого тетракис-шестигранника равна 3/2, а более длинных — 2. Грани представляют собой острые равнобедренные треугольники. Больший из них угол равен $\arccos {\tfrac {1}{9}}\approx 83.62^{\circ }$ и два меньших равны $\arccos {\tfrac {2}{3}}\approx 48.19^{\circ }$ .

Ортогональные проекции

Тетракис -шестигранник , двойственный усеченному октаэдру , имеет три положения симметрии: два расположены в вершинах и одно в середине ребра.

Ортогональные проекции
Проективный симметрия	[2]	[4]	[6]
Тетракис шестигранник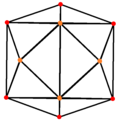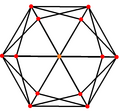
Усечено октаэдр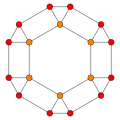

Использование

Природные ( кристаллические ) образования тетрагексаэдров наблюдаются в медных и флюоритовых системах.

многогранные игральные кости иногда используют Игроки в форме тетракис-шестигранника .

, 24-ячеечная структура «сначала вершина», рассматриваемая в перспективной проекции имеет топологию поверхности тетракис-гексаэдра и геометрические пропорции ромбического додекаэдра с ромбическими гранями, разделенными на два треугольника.

Тетракис-шестигранник является одним из простейших примеров в теории строительства . Рассмотрим риманово симметрическое пространство , ассоциированное с группой SL ₄ ( R ) . Его граница Титса имеет структуру сферического здания , квартиры которого представляют собой двумерные сферы. Разбиение этой сферы на сферические симплексы (камеры) можно получить, взяв радиальную проекцию тетракис-гексаэдра.

Симметрия

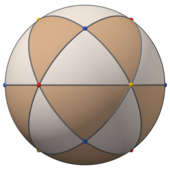
При _{T d} , [3,3] (*332) тетраэдрической симметрии треугольные грани представляют 24 фундаментальные области тетраэдрической симметрии. Этот многогранник можно построить из шести больших кругов на сфере. Его также можно увидеть в виде куба с квадратными гранями, триангулированными вершинами и центрами граней, и тетраэдра, грани которого разделены вершинами, средними ребрами и центральной точкой.


Усечено октаэдр	Дисдякис шестигранник	Дельтовидный додекаэдр

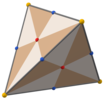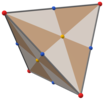ромбический шестигранник	Тетраэдр

Сферический многогранник

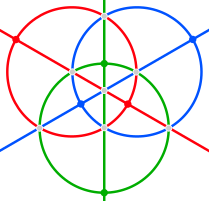
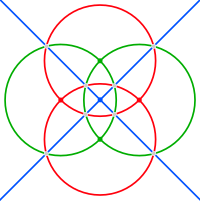
(see rotating model)	Orthographic projections from 2-, 3- and 4-fold axes

Ребра сферического тетракис-шестигранника принадлежат шести большим кругам, которые соответствуют зеркальным плоскостям в тетраэдрической симметрии . Их можно сгруппировать в три пары ортогональных окружностей (каждая из которых обычно пересекается по одной координатной оси). На изображениях ниже эти квадратные осоэдры окрашены в красный, зеленый и синий цвета.

Стереографические проекции
	2-fold	3-fold	4-fold

Размеры

Если мы обозначим длину ребра базового куба через $a$ , высота каждой вершины пирамиды над кубом составит ⁠. ${\tfrac {a}{4}}.$ ⁠ Наклон каждой треугольной грани пирамиды относительно грани куба равен $\arctan {\tfrac {1}{2}}\approx 26.565^{\circ }$ (последовательность A073000 в OEIS ). Одно ребро равнобедренного треугольника имеет длину $a$ , два других — длину ⁠. ${\tfrac {3a}{4}},$ ⁠ что следует из применения теоремы Пифагора к высоте и длине основания. Это дает высоту ${\tfrac {{\sqrt {5}}a}{4}}$ в треугольнике ( OEIS : A204188 ). Его площадь ${\tfrac {{\sqrt {5}}a^{2}}{8}},$ а внутренние углы $\arccos {\tfrac {2}{3}}\approx 48.1897^{\circ }$ и дополнительные $180^{\circ }-2\arccos {\tfrac {2}{3}}\approx 83.6206^{\circ }.$

Объем пирамиды равен ⁠ ${\tfrac {a^{3}}{12}};$ ⁠ поэтому общий объём шести пирамид и куба в шестиграннике равен ⁠ ${\tfrac {3a^{3}}{2}}.$ ⁠

Клитоп

Его можно рассматривать как куб с квадратными пирамидами, покрывающими каждую квадратную грань; то есть это Клитопа куба. Невыпуклая форма этой формы с гранями равностороннего треугольника имеет ту же геометрию поверхности, что и правильный октаэдр , и модель бумажного октаэдра можно повторно сложить в эту форму. ^[4] Эту форму тетракис-гексаэдра проиллюстрировал Леонардо да Винчи в Луки Пачоли ( «Божественной пропорции» 1509). ^[5]

Эту невыпуклую форму тетракис-шестигранника можно сложить вдоль квадратных граней внутреннего куба как сетку четырехмерной кубической пирамиды .

Связанные многогранники и мозаики

Однородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

* n 32 мутация симметрии усеченных мозаик: n .6.6 v т и
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Это многогранники в последовательности, определенной конфигурацией граней V4.6.2 n . Эта группа особенна тем, что имеет все четное количество ребер на вершину и образует биссектрисы, проходящие через многогранники и бесконечные прямые на плоскости, и продолжается в гиперболическую плоскость для любого n ≥ 7.

При четном количестве граней в каждой вершине эти многогранники и мозаики можно показать, чередуя два цвета, чтобы все соседние грани имели разные цвета.

Каждая грань в этих областях также соответствует фундаментальной области группы симметрии с порядками 2,3, n зеркалами в каждой вершине грани треугольника.

* n 32 мутация симметрии всеусеченных мозаик: 4.6.2n v т и
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

См. также

Триаконтаэдр Дисдякиса
Додекаэдр Дисдякиса
Плитка Кисромбилла
Соединение трех октаэдров
Дельтоидный икоситетраэдр , еще одно каталонское тело с 24 гранями.

Ссылки

^ Hexakistetraeder in German, see e.g. Meyers page and Brockhaus page . The same drawing appears in Brockhaus and Efron as преломленный пирамидальный тетраэдр ( refracted pyramidal tetrahedron ).
^ Конвей, Симметрии вещей , стр.284.
^ Лангер, Джоэл К.; Сингер, Дэвид А. (2010), «Размышления о лемнискате Бернулли: сорок восемь граней математической жемчужины», Milan Journal of Mathematics , 78 (2): 643–682, doi : 10.1007/s00032-010- 0124-5 , МР 2781856
^ Рус, Джейкоб (2017), «Flowsnake Earth» , в Сварте, Дэвид; Секин, Карло Х.; Фенивеси, Кристоф (ред.), Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 237–244, ISBN 978-1-938664-22-9
^ Пачоли, Лука (1509), «Таблицы 11 и 12» , Божественная пропорция

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им многогранники, стр. 14, Тетракишегексаэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 [1] (Глава 21, Названия архимедовых и каталонских многогранников и мозаик, страница 284, шестигранник Тетракиса)

Внешние ссылки

Вайсштейн, Эрик В. , « Тетракис шестигранник » (« каталонское тело ») в MathWorld .
Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- VRML Модель
- Обозначение Конвея для многогранников. Попробуйте: «dtO» или «kC».
Тетракис шестигранник – интерактивная модель многогранника.
Однородные многогранники

[1] Hexakistetraeder in German, see e.g. Meyers page and Brockhaus page . The same drawing appears in Brockhaus and Efron as преломленный пирамидальный тетраэдр ( refracted pyramidal tetrahedron ).

[2] Конвей, Симметрии вещей , стр.284.

[3] Лангер, Джоэл К.; Сингер, Дэвид А. (2010), «Размышления о лемнискате Бернулли: сорок восемь граней математической жемчужины», Milan Journal of Mathematics , 78 (2): 643–682, doi : 10.1007/s00032-010- 0124-5 , МР 2781856

[4] Рус, Джейкоб (2017), «Flowsnake Earth» , в Сварте, Дэвид; Секин, Карло Х.; Фенивеси, Кристоф (ред.), Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 237–244, ISBN 978-1-938664-22-9

[5] Пачоли, Лука (1509), «Таблицы 11 и 12» , Божественная пропорция

[1]

[2]

[3]

[4]

[5]