Кубическая пирамида
| Кубическая пирамида | ||
|---|---|---|
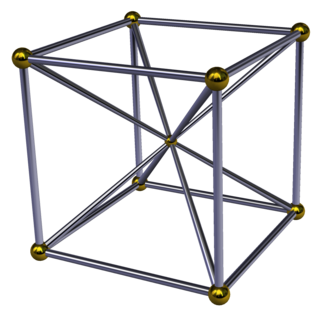 Диаграмма Шлегеля | ||
| Тип | Многогранная пирамида | |
| Символы Шлефли | ( ) ∨ {4,3} ( ) ∨ [{4} × { }] ( ) ∨ [{ } × { } × { }] | |
| Клетки | 7 | 1 {4,3}  6 ( ) ∨ {4}  |
| Лица | 18 | 12 {3} 6 {4} |
| Края | 20 | |
| Вершины | 9 | |
| Двойной | Октаэдрическая пирамида | |
| Группа симметрии | B 3 , [4,3,1], порядок 48 [4,2,1], порядок 16 [2,2,1], порядок 8 | |
| Характеристики | выпуклый , с правильным лицом | |
| Сеть |  | |
В четырехмерной геометрии кубическая пирамида ограничена одним кубом в основании и шестью квадратными ячейками пирамиды , соединяющимися на вершине. Поскольку у куба радиус описанной окружности, разделенный на длину ребра, меньше единицы, [1] квадратные пирамиды можно сделать с правильными гранями, вычислив соответствующую высоту.
Изображения
[ редактировать ]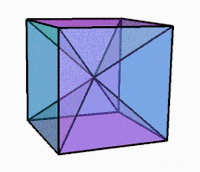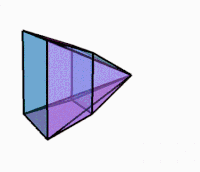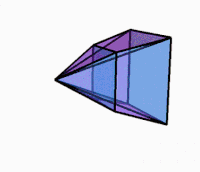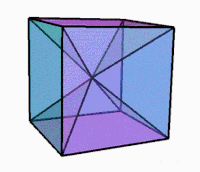 3D-проекция во время вращения |
Связанные многогранники и соты
[ редактировать ]Ровно 8 правильных кубических пирамид соберутся вместе вокруг вершины в четырехмерном пространстве (вершины каждой пирамиды). Эта конструкция дает тессеракт с 8 кубическими ограничивающими ячейками, окружающими центральную вершину с 16 длинными радиусами по длине ребра. Тессеракт мозаизирует четырехмерное пространство в виде тессерактических сот . Четырехмерное содержимое тессеракта с единичной длиной ребра равно 1, поэтому содержимое правильной кубической пирамиды равно 1/8.
Обычная 24-ячеечная структура имеет кубические пирамиды вокруг каждой вершины. Размещение 8 кубических пирамид на кубических ограничивающих ячейках тессеракта - это конструкция Госсета. [2] из 24-клеток. Таким образом, 24-ячеечная пирамида состоит ровно из 16 кубических пирамид. 24-ячеечная мозаика представляет собой 4-мерное пространство в виде сот из 24 ячеек .
Двойственной кубической пирамиде является октаэдрическая пирамида , рассматриваемая как октаэдрическое основание и 8 правильных тетраэдров, встречающихся на вершине.
Кубическую пирамиду нулевой высоты можно рассматривать как куб, разделенный на 6 квадратных пирамид с центральной точкой. Эти квадратные кубы, заполненные пирамидами, могут мозаично формировать трехмерное пространство как двойник усеченных кубических сот , называемых кубическими сотами гексакиса или пирамидиллами .
Кубическую пирамиду можно сложить из трехмерной сетки в виде невыпуклого тетракис-шестигранника , полученного путем наклеивания квадратных пирамид на грани куба, и сложить по квадратам, где пирамиды соприкасаются с кубом.
Ссылки
[ редактировать ]- ^ Клитцинг, Ричард. «3D выпуклые однородные многогранники o3o4x — куб» . кврт(3)/2 = 0,866025
- ^ Коксетер, HSM (1973). Правильные многогранники (Третье изд.). Нью-Йорк: Дувр. п. 150.
Внешние ссылки
[ редактировать ]- Ольшевский, Георгий. «Пирамида» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Клитцинг, Ричард. «4D Сегментотопы» . Клитцинг, Ричард. «Сегментотопный кубик, К-4,26» .
- Ричард Клитцинг, Осесимметричные грани однородных многогранников
 | Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее . |