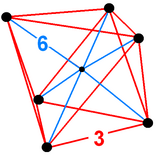
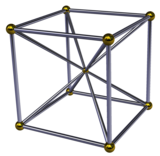
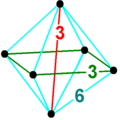
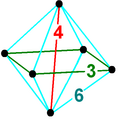
Октаэдрическая пирамида

Октаэдрическая пирамида
Диаграмма Шлегеля
Тип	Многогранная пирамида
Символ Шлефли	( ) ∨ {3,4} ( ) ∨ r{3,3} ( ) ∨ s{2,6} ( ) ∨ [{4} + { }] ( ) ∨ [{ } + { } + { }]
Клетки	9	1 {3,4} 8 ( ) ∨ {3}
Лица	20 {3}
Края	18
Вершины	7
Двойной	Кубическая пирамида
Группа симметрии	B ₃ , [4,3,1], порядок 48 [3,3,1], порядок 24 [2 ⁺,6,1], порядок 12 [4,2,1], порядок 16 [2,2,1], порядок 8
Характеристики	выпуклый , правильные ячейки, слепой многогранник

В 4-мерной геометрии октаэдрическая пирамида ограничена одним октаэдром в основании и 8 треугольными ячейками пирамиды , которые встречаются на вершине. Поскольку октаэдр имеет радиус описанной окружности, разделенный на длину ребра меньше единицы, ^[1] треугольные пирамиды можно сделать с правильными гранями (как правильные тетраэдры ), вычислив соответствующую высоту.

Имея все правильные ячейки, это Слепой многогранник . Две копии можно дополнить, чтобы получилась октаэдрическая бипирамида , которая также является слепым многогранником.

Появления октаэдрической пирамиды

Правильный 16-ячеечный объект имеет восьмигранные пирамиды вокруг каждой вершины, причем октаэдр проходит через центр 16-ячеечного. Таким образом, размещение двух правильных октаэдрических пирамид основанием к основанию образует 16-ячеечную пирамиду. 16-ячеечная мозаика представляет собой 4-мерное пространство в виде сот из 16 ячеек .

Ровно 24 правильные октаэдрические пирамиды соберутся вместе вокруг вершины в четырехмерном пространстве (вершины каждой пирамиды). Эта конструкция дает 24 ячейки с октаэдрическими ограничивающими ячейками, окружающими центральную вершину с 24 длинными радиусами по длине ребра. Четырехмерное содержимое 24-ячейки с единичным ребром равно 2, поэтому содержимое правильной октаэдрической пирамиды равно 1/12. 24-ячеечная мозаика представляет собой 4-мерное пространство в виде сот из 24 ячеек .

Октаэдрическая пирамида — вершинная фигура усечённого 5-ортоплекса , .

Граф октаэдрической пирамиды — единственно возможный минимальный контрпример к гипотезе Негами о том, что связные графы с плоскими покрытиями сами по себе являются проективно-планарными. ^[2]

Пример 4-мерных координат, 6 точек в первых 3 координатах куба и 4-м измерении вершины.

(±1, 0, 0; 0)

( 0,±1, 0; 0)

( 0, 0,±1; 0)

( 0, 0, 0; 1)

Другие многогранники

Кубическая пирамида

Двойной октаэдрической пирамиде является кубическая пирамида , рассматриваемая как кубическое основание и 6 квадратных пирамид, встречающихся на вершине .

Пример 4-мерных координат, 8 точек в первых 3 координатах куба и 4-м измерении вершины.

(±1,±1,±1; 0)

( 0, 0, 0; 1)

Квадратно-пирамидальная пирамида

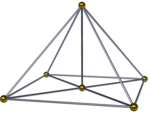
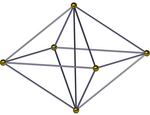
Квадратно-пирамидальная пирамида

Тип	Многогранная пирамида
Символ Шлефли	( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }]
Клетки	6	2 ( )∨{4} 4 ( )∨{3}
Лица	12 {3} 1 {4}
Края	13
Вершины	6
Двойной	Самодвойственный
Группа симметрии	[4,1,1], порядок 8 [4,2,1], порядок 16 [2,2,1], порядок 8
Характеристики	выпуклый , с правильным лицом

Квадратно -пирамидальная пирамида , ( ) ∨ [( ) ∨ {4}], представляет собой разделенную пополам октаэдрическую пирамиду. У него есть квадратное основание пирамиды и 4 тетраэдра, а также еще одна квадратная пирамида, встречающаяся на вершине. Ее также можно увидеть в проекции с центром по ребру как квадратную бипирамиду с четырьмя тетраэдрами, обернутыми вокруг общего ребра. Если высота двух вершин одинакова, ему можно дать более высокое имя симметрии [( ) ∨ ( )] ∨ {4} = { } ∨ {4}, соединяющее ребро с перпендикулярным квадратом. ^[3]

Квадратно -пирамидальная пирамида может быть искажена в прямоугольно-пирамидальную пирамиду , { } ∨ [{ } × { }] или в ромбически-пирамидальную пирамиду , { } ∨ [{ } + { }], или в другие формы более низкой симметрии.

Квадратно -пирамидальная пирамида существует как вершинная фигура в однородных многогранниках вида , включая усеченный 5-ортоплекс и усеченные тессерактические соты .