16-ячеечный

16-ячеечный
(4-ортоплекс)
16-ячеечный ; (4-ортоплекс)
	Диаграмма Шлегеля ; (вершины и ребра)
Тип	Выпуклый правильный 4-многогранник ; 4- ортоплекс ; 4- демикуб
Символ Шлефли	{3,3,4}
Диаграмма Кокстера
Клетки	16 {3,3}
Лица	32 {3}
Края	24
Вершины	8
Вершинная фигура	; Октаэдр
Полигон Петри	восьмиугольник
Группа Коксетера	B 4 , [3,3,4], порядок 384 ; Д 4 , заказ 192
Двойной	Тессеракт
Характеристики	выпуклый , изогональный , изотоксальный , изоэдральный , правильный , многогранник Ханнера
Единый индекс	12

В геометрии — 16-ячейка это правильный выпуклый 4-многогранник (четырёхмерный аналог платонова тела) с символом Шлефли {3,3,4}. Это один из шести правильных выпуклых 4-многогранников, впервые описанных швейцарским математиком Людвигом Шлефли в середине 19 века. ^[1] Его еще называют С ₁₆ , гексадекахорон . ^[2] или гексдекаэдроид [ так в оригинале ? ] . ^[3]

Это 4-мерный член бесконечного семейства многогранников, называемых кросс-многогранниками , ортоплексами или гипероктаэдрами, которые аналогичны октаэдру в трех измерениях. Это Коксетер $\beta _{4}$ многогранник. ^[4] Двойственный многогранник — это тессеракт (4- куб ), с которым его можно объединить, образуя составную фигуру . Ячейки 16-ячейки двойственны 16 вершинам тессеракта.

Геометрия [ править ]

16-клеточный является вторым в последовательности 6 выпуклых правильных 4-многогранников (в порядке размера и сложности). ^[а]

Каждый из его 4-х последующих выпуклых правильных 4-многогранников может быть построен как выпуклая оболочка многогранника, состоящего с 16 вершинами из нескольких 16-ячеек: тессеракт как соединение двух 16-ячеек, 24-вершинный 24- клеточный соединение трех 16-ячеек, 120-вершинная 600-ячейка как соединение пятнадцати 16-ячеек и 600-вершинная 120-ячейка как соединение семидесяти пяти 16-ячеек. ^[б]

Правильные выпуклые 4-многогранники
Symmetry group	A₄	B₄		F₄	H₄
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2	𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2	𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon x 2	1 octagon x 3	2 octagons x 4	2 dodecagons x 4	4 30-gons x 6	20 30-gons x 4
Long radius	$1$	$1$	$1$	$1$	$1$	$1$
Edge length	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\phi }}\approx 0.618$	${\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270$
Short radius	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$
Area	$10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825$	$32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713$	$24$	$96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569$	$1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48$	$720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366$
Volume	$5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329$	$16\left({\tfrac {1}{3}}\right)\approx 5.333$	$8$	$24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314$	$600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693$	$120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118$
4-Content	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193$

Координаты [ править ]

Непересекающиеся квадраты

ху плоскость
( 0, 1, 0, 0)	( 0, 0,-1, 0)
( 0, 0, 1, 0)	( 0,-1, 0, 0)

wz самолет
( 1, 0, 0, 0)	( 0, 0, 0,-1)
( 0, 0, 0, 1)	(-1, 0, 0, 0)

16-ячейка представляет собой 4-мерный перекрестный многогранник (4-ортоплекс) , что означает, что его вершины лежат в противоположных парах на 4 осях декартовой системы координат (w, x, y, z).

Восемь вершин: (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). Все вершины соединены ребрами, кроме противоположных пар. Длина ребра равна √ 2 .

Координаты вершин образуют 6 ортогональных центральных квадратов, лежащих в 6 координатных плоскостях. Квадраты в противоположных плоскостях, не имеющих общей оси (например, в плоскостях xy и wz ), полностью не пересекаются (они не пересекаются ни в каких вершинах). ^[с]

16-ячейка представляет собой ортонормированную основу для выбора 4-мерной системы отсчета, поскольку ее вершины точно определяют четыре ортогональные оси.

Структура [ править ]

Символ Шлефли 16-ячеечной ячейки — {3,3,4}, что указывает на то, что ее ячейки представляют собой правильные тетраэдры {3,3}, а ее вершинная фигура — правильный октаэдр {3,4}. В каждой вершине сходятся 8 тетраэдров, 12 треугольников и 6 ребер. Его краевая фигура представляет собой квадрат. На каждом ребре сходятся 4 тетраэдра и 4 треугольника.

16-ячейка ограничена 16 ячейками , все из которых представляют собой правильные тетраэдры . ^[и] Он имеет 32 треугольные грани , 24 ребра и 8 вершин . 24 ребра ограничивают 6 ортогональных центральных квадратов, лежащих на больших кругах в 6 координатных плоскостях (3 пары полностью ортогональных ^[ф] большие квадраты). В каждой вершине перпендикулярно пересекаются 3 больших квадрата. Шесть ребер встречаются в вершине так же, как шесть ребер встречаются в вершине канонической октаэдрической пирамиды . ^[д] 6 ортогональных центральных плоскостей 16-ячеечной ячейки можно разделить на 4 ортогональные центральные гиперплоскости (3-пространства), каждая из которых образует октаэдр с 3 ортогональными большими квадратами.

Ротации [ править ]

3D-проекция 16-клеточного элемента, выполняющего простое вращение.	3D-проекция 16-клеточной клетки, совершающей двойное вращение.

Вращения в 4-мерном евклидовом пространстве можно рассматривать как композицию двух 2-мерных вращений в полностью ортогональных плоскостях. ^[6] 16-ячеечная система представляет собой простую систему координат, в которой можно наблюдать четырехмерное вращение, поскольку у каждого из 6 больших квадратов 16-ячеечной клетки есть еще один полностью ортогональный большой квадрат (есть 3 пары полностью ортогональных квадратов). ^[с] Многие вращения 16-ячейки можно охарактеризовать углом поворота в одной из ее плоскостей большого квадрата (например, плоскости xy ) и другим углом поворота в полностью ортогональной плоскости большого квадрата ( плоскости wz ). ^[Дж] Полностью ортогональные большие квадраты имеют непересекающиеся вершины: 4 из 8 вершин 16-клеточного элемента вращаются в одной плоскости, а остальные 4 вращаются независимо в полностью ортогональной плоскости. ^[г]

В 2-х или 3-х измерениях вращение характеризуется одной плоскостью вращения; такой вид вращения, происходящий в 4-мерном пространстве, называется простым вращением , при котором вращается только одна из двух полностью ортогональных плоскостей (угол вращения в другой плоскости равен 0). В 16-ячейке простое вращение в одной из 6 ортогональных плоскостей перемещает только 4 из 8 вершин; остальные 4 остаются фиксированными. (В приведенной выше простой анимации вращения все 8 вершин перемещаются, поскольку плоскость вращения не является одной из 6 ортогональных базисных плоскостей.)

При двойном вращении оба набора из 4 вершин движутся, но независимо: углы поворота могут быть разными в двух полностью ортогональных плоскостях. Если два угла совпадают, максимально симметричное изоклиническое вращение . происходит ^[д] В 16-ячейке изоклинический поворот на 90 градусов любой пары полностью ортогональных квадратных плоскостей переводит каждую квадратную плоскость в ее полностью ортогональную квадратную плоскость. ^[р]

Конструкции [ править ]

Октаэдрическая дипирамида [ править ]

Октаэдр $\beta _{3}$	16-ячеечный $\beta _{4}$

Ортогональные проекции для перекоса гиперплоскости шестиугольника

Простейшая конструкция 16-ячеечного трехмерного перекрестного многогранника — октаэдра . Октаэдр имеет 3 перпендикулярные оси и 6 вершин в 3 противоположных парах (его многоугольник Петри — шестиугольник ). Добавьте еще одну пару вершин на четвертой оси, перпендикулярной всем трем другим осям. Соедините каждую новую вершину со всеми 6 исходными вершинами, добавив 12 новых ребер. Это поднимает две октаэдрические пирамиды на общем основании октаэдра, которое лежит в центральной гиперплоскости 16 ячеек. ^[10]

Октаэдр, с которого начинается построение, имеет три перпендикулярно пересекающихся квадрата (которые в шестиугольных проекциях выглядят как прямоугольники). Каждый квадрат пересекается с каждым другим квадратом в двух противоположных вершинах, причем в каждой вершине пересекаются два квадрата. Затем добавляются еще две точки в четвертом измерении (выше и ниже трехмерной гиперплоскости). Эти новые вершины соединяются со всеми вершинами октаэдра, создавая 12 новых ребер и еще три квадрата (которые выглядят с ребра как три диаметра шестиугольника в проекции) и еще три октаэдра. ^[час]

Создано и нечто беспрецедентное. Обратите внимание, что каждый квадрат больше не пересекается со всеми другими квадратами: он пересекается с четырьмя из них ( теперь три квадрата пересекаются в каждой вершине), но у каждого квадрата есть еще один квадрат, с которым у него нет общих вершин: это вообще не связан напрямую с этой площадью. Эти два отдельных перпендикулярных квадрата (их три пары) подобны противоположным ребрам тетраэдра : перпендикулярны, но непересекающиеся. Они лежат друг против друга (в некотором смысле параллельно) и не соприкасаются, но и проходят друг через друга, как два перпендикулярных звена цепи (но в отличие от звеньев цепи имеют общий центр). Они являются примером параллельных плоскостей Клиффорда , а 16-клеточный — простейший правильный многогранник, в котором они встречаются. Клиффордский параллелизм ^[л] объектов более чем одного измерения (больше, чем просто изогнутые линии ) появляется здесь и встречается во всех последующих 4-мерных правильных многогранниках, где его можно рассматривать как определяющее отношение между непересекающимися концентрическими правильными 4-многогранниками и их соответствующими частями. Это может произойти между конгруэнтными (похожими) многогранниками двух или более измерений. ^[11] Например, как отмечалось выше , все последующие выпуклые правильные 4-многогранники представляют собой соединения нескольких 16-клеток; эти 16 ячеек представляют собой параллельные многогранники Клиффорда .

Тетраэдрические конструкции [ править ]

16-ячеечная структура имеет две конструкции Витхоффа из правильных тетраэдров, правильную форму и чередующуюся форму, показанные здесь в виде сеток , вторая представлена тетраэдрическими ячейками двух чередующихся цветов. Альтернативная форма представляет собой конструкцию с более низкой симметрией из 16 ячеек, называемую демитессерактом .

Конструкция Витхоффа повторяет характерную 16-ячеечную 5-ячеечную систему в калейдоскопе зеркал. Каждый правильный 4-многогранник имеет свою характерную 4-ортосхему — неправильную 5-клеточную . ^[с] Существует три правильных 4-многогранника с тетраэдрическими ячейками: 5-ячеечный , 16-ячеечный и 600-ячеечный . Хотя все они ограничены правильными ячейками тетраэдра, их характерные 5-ячейки (4-ортосхемы) представляют собой разные тетраэдрические пирамиды , основанные на одном и том же характерном неправильном тетраэдре. Они имеют одинаковый характерный тетраэдр (3-ортосхема) и характерный прямоугольный треугольник (2-ортосхема), поскольку имеют одинаковый тип ячеек. ^[т]

Характеристики 16-ячеечного ^[13]
	край ^[14]	дуга		двугранный ^[15]
𝒍	${\sqrt {2}}\approx 1.414$	90°	${\tfrac {\pi }{2}}$	120°	${\tfrac {2\pi }{3}}$

𝟀	${\sqrt {\tfrac {2}{3}}}\approx 0.816$	60″	${\tfrac {\pi }{3}}$	60°	${\tfrac {\pi }{3}}$
𝝉 ^[в]	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	45″	${\tfrac {\pi }{4}}$	45°	${\tfrac {\pi }{4}}$
𝟁	${\sqrt {\tfrac {1}{6}}}\approx 0.408$	30″	${\tfrac {\pi }{6}}$	60°	${\tfrac {\pi }{3}}$

$_{0}R^{3}/l$	${\sqrt {\tfrac {3}{4}}}\approx 0.866$	60°	${\tfrac {\pi }{3}}$	90°	${\tfrac {\pi }{2}}$
$_{1}R^{3}/l$	${\sqrt {\tfrac {1}{4}}}=0.5$	45°	${\tfrac {\pi }{4}}$	90°	${\tfrac {\pi }{2}}$
$_{2}R^{3}/l$	${\sqrt {\tfrac {1}{12}}}\approx 0.289$	30°	${\tfrac {\pi }{6}}$	90°	${\tfrac {\pi }{2}}$

$_{0}R^{4}/l$	$1$
$_{1}R^{4}/l$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$
$_{2}R^{4}/l$	${\sqrt {\tfrac {1}{3}}}\approx 0.577$
$_{3}R^{4}/l$	${\sqrt {\tfrac {1}{4}}}=0.5$

Характеристика 5-клетки обычной 16-клетки представлена диаграммой Кокстера-Дынкина. , который можно прочитать как список двугранных углов между его зеркальными гранями. Это неправильная тетраэдрическая пирамида, основанная на характерном тетраэдре правильного тетраэдра . Обычная 16-ячеечная структура подразделяется своими гиперплоскостями симметрии на 384 экземпляра характерной 5-ячеечной клетки, которые все встречаются в ее центре.

Характеристическая 5-ячейка (4-ортосхема) имеет на четыре ребра больше, чем ее базовый характеристический тетраэдр (3-ортосхема), соединяя четыре вершины основания с ее вершиной (пятая вершина 4-ортосхемы, в центре обычный 16-клеточный). ^[v] Если обычная 16-ячейка имеет ребро единичного радиуса и длину ребра 𝒍 = ${\sqrt {2}}$ , десять ребер его характерной 5-ячейки имеют длину ${\sqrt {\tfrac {2}{3}}}$ , ${\sqrt {\tfrac {1}{2}}}$ , ${\sqrt {\tfrac {1}{6}}}$ вокруг его внешней грани прямоугольного треугольника (ребра, противоположные характерным углам 𝟀, 𝝉, 𝟁), ^[в] плюс ${\sqrt {\tfrac {3}{4}}}$ , ${\sqrt {\tfrac {1}{4}}}$ , ${\sqrt {\tfrac {1}{12}}}$ (остальные три ребра внешней 3-ортосхемы ограняют характеристический тетраэдр, которые являются характеристическими радиусами правильного тетраэдра), плюс $1$ , ${\sqrt {\tfrac {1}{2}}}$ , ${\sqrt {\tfrac {1}{3}}}$ , ${\sqrt {\tfrac {1}{4}}}$ (ребра — характерные радиусы правильной 16-ячеечной ячейки). Путь с 4 ребрами вдоль ортогональных ребер ортосхемы равен ${\sqrt {\tfrac {1}{2}}}$ , ${\sqrt {\tfrac {1}{6}}}$ , ${\sqrt {\tfrac {1}{4}}}$ , ${\sqrt {\tfrac {1}{4}}}$ , сначала от вершины с 16 ячейками к центру ребра с 16 ячейками, затем поворот на 90 ° к центру грани с 16 ячейками, затем поворот на 90 ° к центру тетраэдрической ячейки с 16 ячейками, затем поворот на 90 ° к центру 16-ячеечной ячейки центр.

Спиральная конструкция [ править ]

16-ячеечную структуру можно построить (тремя различными способами) из двух спиралей Бурдейка – Кокстера из восьми связанных тетраэдров, каждый из которых согнут в четвертом измерении в кольцо. ^[16]^[17] Две круговые спирали закручиваются вокруг друг друга, вкладываются друг в друга и проходят друг через друга, образуя звено Хопфа . 16 треугольных граней можно увидеть в 2D-сети внутри треугольной мозаики с 6 треугольниками вокруг каждой вершины. Фиолетовые края представляют собой многоугольник Петри из 16 ячеек. Восьмиклеточное кольцо тетраэдров содержит три октаграммы разного цвета, восьмиреберные круговые пути, дважды обвивающие 16-клетку в каждой третьей вершине октаграммы. Оранжевый и желтый края представляют собой две четырехгранные половинки одной октаграммы, которые соединяются своими концами, образуя ленту Мёбиуса .

Таким образом, 16-ячеечную структуру можно разложить на две непересекающиеся круговые цепочки по восемь тетраэдров каждая, с четырьмя ребрами в длину, одна из которых закручивается по спирали вправо (по часовой стрелке), а другая закручивается по спирали влево (против часовой стрелки). Левое и правое клеточные кольца подходят друг к другу, вложенные друг в друга и полностью заполняющие 16-клетку, хотя они имеют противоположную хиральность. Это разложение можно увидеть в конструкции дуоантипризмы 4-4 из 16 ячеек: или , символ Шлефли {2}⨂{2} или s{2}s{2}, симметрия [4,2 ⁺,4], порядок 64.

Три пути из восьми ребер (разных цветов) проходят по спирали вдоль каждого кольца из восьми ячеек, образуя углы 90 ° в каждой вершине. (В спирали Бурдейка – Кокстера до того, как она согнута в кольцо, углы на разных путях различаются, но не составляют 90 °.) Через каждую вершину проходят три пути (с тремя разными цветами и видимыми углами). Когда спираль сгибается в кольцо, отрезки каждого восьмиреберного пути (разной длины) соединяются своими концами, образуя ленту Мёбиуса длиной восемь ребер вдоль ее односторонней окружности 4 и шириной в одно ребро. ^[п] Каждая из шести четырехгранных половин трех восьмиреберных путей образует четыре угла по 90°, но они не являются шестью ортогональными большими квадратами: это квадраты с открытыми концами, четырехгранные спирали на 360°, открытые концы которых являются противоположными вершинами. Четыре ребра исходят из четырех разных больших квадратов и взаимно ортогональны. Объединенные сквозными парами одинаковой киральности , шесть четырехреберных путей образуют три восьмиреберные петли Мёбиуса, спиральные октаграммы. Каждая октаграмма представляет собой одновременно многоугольник Петри 16 ячеек из 16 ячеек и спиральную дорожку, вдоль которой все восемь вершин вращаются вместе, в одном из различных изоклинических вращений . ^[В]

Пять способов взглянуть на одну и ту же перекошенную октаграмму ^[х]
Краевой путь	Полигон Петри ^[18]	16-ячеечный	Дискретное расслоение	Диаметр хорд
Октаграмма _{8/3}^[19]	Октаграмма _{8/1}	Самолет Коксетера B ₄	Октаграмма _{8/2}=2{4}	Октаграмма _{8/4}=4{2}

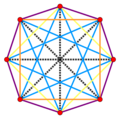Восемь √ 2 хорд ребра изоклины. ^[и]	Косой восьмиугольник из восьми √ 2 ребер. В 16-ячейке есть 3 из этих 8-вершинных контуров.	Все 24 √ 2 ребра и четыре √ 4 ортогональные оси.	Два полностью ортогональных (непересекающихся) больших квадрата с √ 2 ребрами. ^[г]	Четыре √ 4 хорды изоклины. Каждая четвертая вершина изоклины соединена со своей антиподальной вершиной 16-ячеечной осью. ^[и]

Каждая восьмиреберная спираль представляет собой косую октаграмму _{8/3} , которая трижды обвивает 16-ячейку и посещает каждую вершину, прежде чем замкнуться в петлю. Его восемь √ 2 ребер представляют собой хорды изоклины , винтовой дуги, на которой 8 вершин вращаются во время изоклинического вращения. ^[п] Все восемь 16-клеточных вершин находятся на расстоянии √ 2 друг от друга, за исключением противоположных (антиподальных) вершин, которые находятся на расстоянии √ 4 друг от друга. Вершина, движущаяся по изоклине, посещает три другие вершины, находящиеся на расстоянии √ 2 друг от друга, прежде чем достичь четвертой вершины, находящейся на расстоянии √ 4 друг от друга. ^[the]

Кольцо из восьми ячеек является хиральным : существует правая форма, которая закручивается по спирали по часовой стрелке, и левая форма, которая закручивается по спирали против часовой стрелки. 16-ячейка содержит по одному каждому из них, поэтому она также содержит левую и правую изоклины; изоклина — это круговая ось, вокруг которой закручивается кольцо из восьми ячеек. Каждая изоклина посещает все восемь вершин 16-ячейки. ^[аб] Каждое кольцо из восьми ячеек содержит половину из 16 ячеек, но все 8 вершин; два кольца имеют общие вершины, поскольку они вложены друг в друга и подходят друг к другу. Они также имеют общие 24 ребра, хотя левая и правая спирали октаграмм представляют собой разные пути с восемью ребрами. ^[и]

Поскольку существуют три пары полностью ортогональных больших квадратов, ^[с] существует три конгруэнтных способа составить 16-клеточное кольцо из двух восьмиклеточных колец. 16-ячеечная структура содержит три левые-правые пары восьмиклеточных колец в разных ориентациях, причем каждое клеточное кольцо содержит свою осевую изоклину. ^[В] Каждая левая-правая пара изоклин является следом пары левых-правых различных изоклинических вращений: вращений в одной паре полностью ортогональных инвариантных плоскостей вращения. ^[г] В каждой вершине есть три больших квадрата и шесть изоклин октаграмм, которые пересекаются в вершине и имеют общую хорду оси из 16 ячеек. ^{[объявление]}

В качестве конфигурации [ править ]

Эта матрица конфигурации представляет собой 16 ячеек. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько каждого элемента встречается во всей 16-ячейке. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним.

${\begin{bmatrix}{\begin{matrix}8&6&12&8\\2&24&4&4\\3&3&32&2\\4&6&4&16\end{matrix}}\end{bmatrix}}$

Тесселяции [ править ]

можно замостить Четырехмерное евклидово пространство обычными 16 ячейками. Это называется сотами из 16 ячеек и имеет символ Шлефли {3,3,4,3}. Следовательно, 16-ячеечная структура имеет двугранный угол 120°. ^[21] Каждая 16-ячейка имеет 16 соседей, с которыми она делит тетраэдр, 24 соседа, с которыми она разделяет только ребро, и 72 соседа, с которыми она разделяет только одну точку. Двадцать четыре 16-ячейки встречаются в любой вершине этой мозаики.

Двойная мозаика, соты из 24 ячеек , {3,4,3,3}, состоят из обычных 24 ячеек . Вместе с тессерактическими сотами {4,3,3,4} это единственные три мозаики R. правильные ⁴.

Прогнозы [ править ]

орфографические проекции
Самолет Коксетера	Б ₄	Б ₃ / Д ₄ / А ₂	Б2 / _Д3
График
Двугранная симметрия	[8]	[6]	[4]
Самолет Коксетера	F_F4	A_А3
График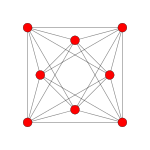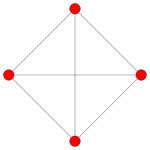
Двугранная симметрия	[12/3]	[4]

Параллельная проекция 16-ячеечной ячейки в трехмерное пространство имеет кубическую оболочку. Ближайшие и самые дальние ячейки проецируются на вписанные тетраэдры внутри куба, что соответствует двум возможным способам вписания правильного тетраэдра в куб. Каждый из этих тетраэдров окружают 4 других (неправильных) тетраэдрических объема, которые являются изображениями 4 окружающих тетраэдрических ячеек, заполняя пространство между вписанным тетраэдром и кубом. Остальные 6 ячеек проецируются на квадратные грани куба. В этой проекции 16-ячейки все ее ребра лежат на гранях кубической оболочки.

Перспективная проекция 16-клеточной ячейки в 3-мерное пространство имеет триакис-тетраэдрическую оболочку. Расположение ячеек внутри этой оболочки аналогично расположению параллельной проекции «сначала ячейка».

Первичная параллельная проекция 16-ячеечного пространства в 3-мерное пространство имеет октаэдрическую оболочку . Этот октаэдр можно разделить на 8 тетраэдрических объемов, разрезав его по координатным плоскостям. Каждый из этих объемов представляет собой изображение пары ячеек в 16-клеточном пространстве. Ближайшая к зрителю вершина 16-ячейки проецируется на центр октаэдра.

Наконец, параллельная проекция, обращенная к ребру, имеет укороченную октаэдрическую оболочку, а параллельная проекция, обращенная к грани, имеет шестиугольную бипирамидальную оболочку.

4-сферная диаграмма Венна [ править ]

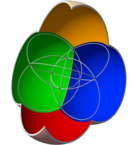
Трехмерная проекция 16 ячеек и 4 пересекающихся сфер ( диаграмма Венна из 4 множеств) топологически эквивалентны.

16 ячеек, упорядоченных по количеству пересекающихся сфер (от 0 до 4) (см. все ячейки и k -грани )

4-сферная диаграмма Венна и 16-ячеечная проекция в одной ориентации

Симметричные конструкции [ править ]

16 ячеек Группа симметрии обозначается B ₄ .

Существует форма более низкой симметрии 16-ячеечной ячейки , называемая демитессерактом или 4-демикубом , членом семейства демигиперкубов и представленная h{4,3,3} и диаграммами Кокстера. или . Его можно нарисовать двухцветным с чередующимися тетраэдрическими ячейками.

Его также можно рассматривать в форме более низкой симметрии как тетраэдрическую антипризму , построенную из двух параллельных тетраэдров в двойной конфигурации, соединенных 8 (возможно, удлиненными) тетраэдрами. Это представлено s{2,4,3} и диаграммой Кокстера: .

Его также можно рассматривать как курносый 4- ортотоп , представленный s{2 ^1,1,1} и диаграмма Кокстера: или .

Поскольку тессеракт 4-4 построен как дуопризма , 16-клеточную можно рассматривать как ее двойник, дуопирамиду 4-4 .

Имя	Диаграмма Кокстера	Символ Шлефли	Обозначение Кокстера	Заказ
Обычный 16-ячеечный		{3,3,4}	[3,3,4]	384
Демитессеракт Квазирегулярный 16-клеточный	= =	ч{4,3,3} {3,3 ^1,1}	[3 ^1,1,1] = [1 ⁺,4,3,3]	192
Чередованная 4-4 дуопризма		2с{4,2,4}	[[4,2 ⁺,4]]	64
Тетраэдрическая антипризма		с{2,4,3}	[2 ⁺,4,3]	48
Призма чередующейся квадратной призмы		ср{2,2,4}	[(2,2) ⁺,4]	16
Курносый 4- ортотоп	=	с{2 ^1,1,1}	[2,2,2] ⁺ = [2 ^1,1,1] ⁺	8
4- винтовка
		{3,3,4}	[3,3,4]	384
		{4}+{4} или 2{4}	[[4,2,4]] = [8,2 ⁺,8]	128
		{3,4}+{ }	[4,3,2]	96
		{4}+2{ }	[4,2,2]	32
		{ }+{ }+{ }+{ } или 4{ }	[2,2,2]	16

Связанные сложные многоугольники [ править ]

Многоугольник Мёбиуса –Кантора — это правильный комплексный многоугольник ₃ {3} ₃ , , в $\mathbb {C} ^{2}$ имеет те же вершины, что и 16-ячеечный. Он имеет 8 вершин и 8 3-ребер. ^[22]^[23]

Правильный комплексный многоугольник, ₂ {4} ₄ , , в $\mathbb {C} ^{2}$ имеет реальное представление в виде 16-клетки в 4-мерном пространстве с 8 вершинами, 16 2-ребрами, лишь половиной ребер 16-клетки. Его симметрия ₄ [4] ₂ , порядок 32. ^[24]

Ортогональные многоугольника ₂ {4} ₄ проекции
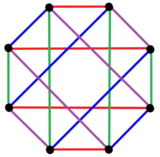В _{B 4} плоскости Кокстера 2 ₄ {4} _{имеет 8 вершин и 16 2-ребер, показанных} здесь в 4 наборах цветов.	8 вершин сгруппированы в 2 набора (показаны красным и синим), каждый из которых соединен только ребрами с вершинами другого набора, что делает этот многоугольник полным двудольным графом K _4,4 . ^[25]

Связанные однородные многогранники и соты [ править ]

Правильный 16-клеточный и тессеракт являются регулярными членами набора из 15 однородных 4-многогранников с одинаковой _{B 4} симметрией . 16-ячеечный также является одним из D ₄ однородных многогранников симметрии .

16-ячеечная структура также связана с кубическими сотами , додекаэдрическими сотами 4-го порядка и гексагональными мозаичными сотами 4-го порядка , все из которых имеют октаэдрические вершинные фигуры .

Он принадлежит к последовательности {3,3,p} 4-многогранников, имеющих тетраэдрические ячейки. Последовательность включает три правильных 4-многогранника евклидова 4-мерного пространства: 5-клеточный {3,3,3}, 16-клеточный {3,3,4} и 600-клеточный {3,3,5}). и тетраэдрические соты 6-го порядка {3,3,6} гиперболического пространства.

Это первая последовательность квазирегулярных многогранников и сот h{4,p,q} и последовательность полусимметрии для правильных форм {p,3,4}.

См. также [ править ]

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

Примечания [ править ]

^ Выпуклые правильные 4-многогранники можно упорядочить по размеру как мере 4-мерного содержимого (гиперобъема) для того же радиуса. Каждый больший многогранник в последовательности более круглый , чем его предшественник, и содержит больше содержимого. ^[5] в том же радиусе. 4-симплекс (5-ячеечный) — это наименьший случай, а 120-ячеечный — самый большой. Сложность (измеряемая путем сравнения матриц конфигурации или просто количества вершин) следует тому же порядку. Это обеспечивает альтернативную схему числового именования для правильных многогранников, в которой 16-ячеечный является 4-многогранником с 8 точками: вторым в возрастающей последовательности, которая проходит от 4-точечного многогранника с 5 точками до 4-многогранника с 600 точками.
^ Есть 2 и только 2 16-клетки, вписанные в 8-клетку (тессеракт), 3 и только 3 16-клетки, вписанные в 24-клетку, 75 отдельных 16-клеток (но только 15 непересекающихся 16-клеток), вписанных в 600-ячеечная и 675 отдельных 16-клеточных (но только 75 непересекающихся 16-клеточных), вписанных в 120-ячеечную.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г В четырехмерном пространстве через точку можно построить 4 перпендикулярные оси и 6 перпендикулярных плоскостей. Без ограничения общности мы можем принять их за оси и ортогональные центральные плоскости декартовой системы координат (w, x, y, z). В 4-х измерениях у нас есть те же 3 ортогональные плоскости (xy, xz, yz), что и в 3-х измерениях, а также еще 3 (wx, wy, wz). Каждая из шести ортогональных плоскостей имеет общую ось с четырьмя другими и противоположна или полностью ортогональна только одной из остальных: единственной, с которой она не имеет общей оси. Таким образом, имеется 3 пары полностью ортогональных плоскостей: xy и wz пересекаются только в начале координат; xz и wy пересекаются только в начале координат; yz и wx пересекаются только в начале координат.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Каждая вершина в 16-ячейке является вершиной октаэдрической пирамиды , основанием которой является октаэдр, образованный 6 другими вершинами, с которыми вершина соединена рёбрами. 16-ячеечную структуру можно разобрать (четырьмя различными способами) на две октаэдрические пирамиды, разрезав ее пополам через одну из четырех октаэдрических центральных гиперплоскостей. Если смотреть изнутри на изогнутый трехмерный объем его граничной поверхности из 16 связанных гранями тетраэдров, вершинная фигура 16-ячеечной структуры представляет собой октаэдр. В четырех измерениях вершинный октаэдр на самом деле представляет собой октаэдрическую пирамиду. Вершина октаэдрической пирамиды (вершина, где встречаются шесть ребер) на самом деле не находится в центре октаэдра: она смещена радиально наружу в четвертом измерении, за пределы гиперплоскости, определяемой шестью вершинами октаэдра. 6 ребер вокруг вершины образуют ортогональный трехосный крест в трех измерениях (и в трехмерной проекции четырехмерной пирамиды ), но три линии фактически согнуты на 90 градусов в четвертом измерении, где они встречаются в вершине. .
^ Граничная поверхность 16-ячейки представляет собой конечное трехмерное пространство, состоящее из 16 тетраэдров, расположенных лицом к лицу (четыре вокруг одного). Это замкнутое, сильно искривленное (неевклидово) трехмерное пространство, внутри которого мы можем двигаться прямо через четыре тетраэдра в любом направлении и вернуться обратно в тот тетраэдр, с которого мы начали. Мы можем визуализировать перемещение внутри этого тетраэдра в джунглях , взбираясь из одного тетраэдра в другой по его 24 стойкам (его краям) и никогда не имея возможности выбраться (или увидеть) из 16 тетраэдров, независимо от того, в каком направлении мы идем (или смотреть). Мы всегда находимся на поверхности 16-клетки (или внутри нее), но никогда внутри самой 16-клетки (ни вне ее). Мы видим, что 6 ребер вокруг каждой вершины расходятся симметрично в трех измерениях и образуют ортогональный трехосный крест, точно так же, как это делают радиусы октаэдра (поэтому мы говорим, что вершинная фигура 16-ячейки - это октаэдр). ^[д]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Две плоские плоскости A и B евклидова четырехмерного пространства называются полностью ортогональными тогда и только тогда, когда каждая прямая в A ортогональна каждой прямой в B. В этом случае плоскости A и B пересекаются в одной точке O, так что если линия в A пересекается с линией в B, они пересекаются в точке O. A и B перпендикулярны и параллельны Клиффорду . ^[с]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Полностью ортогональные большие квадраты не пересекаются и вращаются независимо, поскольку большие круги, на которых лежат их вершины, параллельны Клиффорду . ^[л] Расстояние между ними составляет √ 2 в каждой паре ближайших вершин (а в 16-клетке все пары, кроме антиподальных, ближайшие). Два квадрата вообще не могут пересекаться, поскольку лежат в плоскостях, пересекающихся только в одной точке: центре 16-клетки. ^[с] Поскольку они перпендикулярны и имеют общий центр, два квадрата, очевидно, не параллельны и разделены обычным способом параллельных квадратов в трех измерениях; скорее они связаны как соседние квадратные звенья в цепи, каждое проходит через другое, не пересекаясь ни в каких точках, образуя звено Хопфа .
↑ Перейти обратно: Перейти обратно: ^а ^б В каждой вершине (и в противоположной ей вершине) 16-ячейки встречаются три больших квадрата. У каждого из них есть отдельный полностью ортогональный квадрат. ^[ф] Таким образом, есть три больших квадрата, полностью ортогональных каждой вершине и противоположной ей вершине (каждой оси). Они образуют октаэдр (центральную гиперплоскость). Каждая осевая линия в 16-ячейке полностью ортогональна гиперплоскости центрального октаэдра, так же как каждая плоскость большого квадрата полностью ортогональна другой плоскости большого квадрата. ^[с] Ось и октаэдр пересекаются только в одной точке (центр 16-ячейки), так как каждая пара полностью ортогональных больших квадратов пересекается только в одной точке (центр 16-ячейки). Каждый центральный октаэдр также является октаэдрической фигурой двух из восьми вершин: двух на его полностью ортогональной оси.
^ Три не полностью вершины ортогональных больших квадрата, которые пересекаются в каждой вершине 16-ячейки, образуют октаэдрическую вершинную фигуру . ^[д] Любые два из них вместе с полностью ортогональным квадратом третьего также образуют октаэдр: центральную октаэдрическую гиперплоскость. ^[час] В 16-ячейке каждая октаэдрическая вершина также является центральной октаэдрической гиперплоскостью.
^ Каждая вершина большого квадрата удалена на √ 2 от двух других вершин квадрата и на √ 4 от противоположной вершины. Остальные четыре вершины 16-клетки (также удаленные на √ 2 ) являются вершинами полностью ортогонального квадрата квадрата. ^[г] Каждая вершина из 16 ячеек представляет собой вершину трех пересекающихся ортогональных больших квадратов. У каждого из них есть отдельный полностью ортогональный квадрат. Таким образом, есть три больших квадрата, полностью ортогональных каждой вершине: квадраты, частью которых вершина не является. ^[я]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Каждая большая квадратная плоскость изоклинична (параллель Клиффорда) пяти другим квадратным плоскостям, но полностью ортогональна. ^[ф] только одному из них. Каждая пара полностью ортогональных плоскостей имеет параллельные большие круги Клиффорда, но не все параллельные большие круги Клиффорда ортогональны. Есть еще один способ, по которому полностью ортогональные плоскости входят в выдающуюся категорию параллельных плоскостей Клиффорда: они не являются киральными . Пара изоклинических (параллельных Клиффорда) плоскостей является либо левой парой , либо правой парой , если они не разделены двумя углами 90 ° (полностью ортогональные плоскости) или 0 ° (совпадающие плоскости). ^[20] Большинство изоклинических плоскостей соединяются только за счет левого изоклинического вращения или правого изоклинического вращения соответственно. Полностью ортогональные плоскости являются особенными: пара плоскостей представляет собой одновременно левую и правую пару, поэтому либо левое, либо правое изоклиническое вращение объединит их. Поскольку плоскости, разделенные изоклиническим поворотом на 90 °, находятся на расстоянии 180 ° друг от друга, плоскость слева и плоскость справа являются одной и той же плоскостью. ^[р]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Параллели Клиффорда — это непересекающиеся кривые линии, параллельные в том смысле, что перпендикулярное (кратчайшее) расстояние между ними одинаково в каждой точке. ^[7] Двойная спираль является примером параллелизма Клиффорда в обычном трехмерном евклидовом пространстве. В 4-мерном пространстве параллели Клиффорда представляют собой большие геодезические круги на 3-сфере . ^[8] В 16-ячейке соответствующие вершины полностью ортогональных квадратов большого круга находятся на расстоянии √ 2 друг от друга, поэтому эти квадраты представляют собой параллельные многоугольники Клиффорда. ^[к] Обратите внимание, что только вершины больших квадратов (точки большого круга) находятся на расстоянии √ 2 друг от друга; точки на краях квадратов (на хордах круга) расположены ближе друг к другу.
^ Противоположные вершины 4-многогранника единичного радиуса соответствуют противоположным вершинам 8-клеточного гиперкуба (тессеракта). Длинная диагональ этого радиально равностороннего 4-куба равна √ 4 . При изоклиническом вращении на 90° каждая вершина 16-ячейки смещается к своей антиподальной вершине, путешествуя по винтовой геодезической дуге длиной 𝝅 (180°), к вершине √ 4 по длинному диаметру единичного радиуса 4. -многогранник (16-ячеечный или тессеракт), такое же полное смещение, как если бы он был смещен √ 1 четыре раза, путешествуя по пути из четырех последовательных ортогональных ребер тессеракта.
^ Существует шесть различных путей с двумя ребрами, соединяющих пару противоположных вершин по краям большого квадрата. Левое изоклиническое вращение проходит по диагонали между тремя из них, а правое изоклиническое вращение проходит по диагонали между тремя другими. Эти диагонали представляют собой прямые линии (геодезические), соединяющие противоположные вершины граничных тетраэдрических ячеек в левом восьмиклеточном кольце и правом восьмиклеточном кольце соответственно.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с В 16-ячейке две антиподальные вершины являются противоположными вершинами двух тетраэдрических ячеек, связанных гранями. Две антиподальные вершины соединены (тремя разными) двуреберными путями большого круга вдоль ребер тетраэдрических ячеек, различными трехреберными путями и четырехреберными путями на изоклинах и многоугольниках Петри. ^[п]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Изоклина — это окружность особого вида, соответствующая паре окружностей Вильярсо, связанных в петлю Мёбиуса . Он проходит через четыре измерения вместо двух. Все обычные круги имеют длину окружности 2𝝅, но изоклина из 16 ячеек представляет собой круг с длиной окружности 4𝝅 (более восьми хорд 90°). Изоклина — это круг, который не лежит на плоскости, но во избежание путаницы мы всегда называем ее изоклиной и оставляем термин «круг» для обычного круга на плоскости.
↑ Перейти обратно: Перейти обратно: ^а ^б При изоклиническом вращении все 6 ортогональных плоскостей смещаются сразу в двух ортогональных направлениях: они поворачиваются на один и тот же угол и в то же время наклоняются вбок на тот же угол. Изоклиническое смещение (также известное как смещение Клиффорда ) представляет собой четырехмерную диагональ. Точки смещаются на одинаковое расстояние одновременно в четырех ортогональных направлениях и смещаются на общее пифагорово расстояние, равное квадратному корню из четырехкратного квадрата этого расстояния. Все вершины правильного 4-многогранника смещаются в вершину, расположенную на расстоянии не менее двух ребер. Например, когда 16-ячейка с единичным радиусом изоклинически поворачивается на 90 ° в инвариантной плоскости большого квадрата, она также поворачивается на 90 ° в полностью ортогональной инвариантной плоскости большого квадрата. ^[с] Плоскость большого квадрата также наклоняется на 90°, занимая полностью ортогональную плоскость. (В соответствии с изоклинической симметрией каждый большой квадрат вращается на 90 ° и наклоняется на 90 ° в сторону в свою полностью ортогональную плоскость.) Каждая вершина (в каждом большом квадрате) перемещается к своей противоположной вершине на расстояние √ 1 в каждом из четырех ортогональных направлений. , общее расстояние √ 4 . ^[м] Исходная и смещенная вершины находятся на расстоянии двух длин ребра на три. ^[н] разные пути по двум краям большой площади. Но изоклина (спиральная дуга, по которой вершина следует во время изоклинического вращения) не проходит вдоль ребер: она проходит между этими разными путями ребер по диагонали, по геодезической (кратчайшей дуге) между исходной и смещенной вершинами. ^[the] Эта изоклиническая геодезическая дуга не является сегментом обычного большого круга; он не лежит в плоскости какого-либо большого квадрата. Это винтовая дуга 180°, изгибающаяся по окружности сразу в двух совершенно ортогональных плоскостях. Этот круг Мёбиуса не лежит ни в одной плоскости и не пересекает какие-либо вершины между исходной и смещенной вершиной. ^[п]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Изоклиническое вращение на 90 градусов двух полностью ортогональных плоскостей приводит их друг к другу. При таком вращении жесткой 16-клетки все 6 ортогональных плоскостей поворачиваются на 90 градусов, а также наклоняются вбок на 90 градусов до их полной ортогонализации (параллели Клиффорда). ^[л] самолет. ^[9] Соответствующие вершины двух полностью ортогональных больших квадратов находятся на расстоянии √ 4 (180 °) друг от друга; большие квадраты (параллельные многогранники Клиффорда) находятся на расстоянии √ 4 (180 °) друг от друга; но две полностью ортогональные плоскости находятся на расстоянии 90 ° друг от друга в двух ортогональных углах, которые их разделяют. Если изоклиническое вращение продолжится еще на 90°, каждая вершина завершит поворот на 360°, и каждый большой квадрат вернется в свою исходную плоскость, но в другой ориентации (поменялись оси): он был перевернут «вверх тормашками» на поверхности 16-ячеечный (который теперь «наизнанку»). Продолжение второго изоклинического поворота на 360° (через четыре изоклинических шага 90° на 90°, поворот на 720°) возвращает все в исходное место и ориентацию.
^ Ортосхема киральный — это неправильный симплекс с прямоугольными гранями , который характерен для некоторого многогранника, если он точно заполняет этот многогранник отражениями себя в своих собственных гранях (его зеркальных стенках ). Каждый правильный многогранник можно разрезать радиально на экземпляры его характерной ортосхемы, окружающей его центр. Характеристическая ортосхема имеет форму, описываемую той же диаграммой Кокстера-Дынкина, что и правильный многогранник без образующего точечного кольца.
^ Правильный многогранник размерности k имеет характеристическую k -ортосхему, а также характеристическую ( k -1)-ортосхему. Правильный 4-многогранник имеет характерную 5-ячейку (4-ортосхему), на которую он подразделяется своими (3-мерными) гиперплоскостями симметрии, а также характерный тетраэдр (3-ортосхему), на который подразделяется его поверхность (2-мерные) плоскости симметрии ячеек. После разделения его (3-мерной) поверхности на характеристические тетраэдры, окружающие центр каждой ячейки, его (4-мерную) внутреннюю часть можно разделить на характеристические 5-ячейки путем добавления радиусов, соединяющих вершины характеристических тетраэдров поверхности с центром 4-мерного многогранника. ^[12] Образовавшиеся таким образом внутренние тетраэдры и треугольники также будут ортосхемами.
↑ Перейти обратно: Перейти обратно: ^а ^б ( Коксетер 1973 ) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы переворачиваем соглашения Кокстера и используем 𝝉 для обозначения характеристического угла.
^ Четыре ребра каждой 4-ортосхемы, которые встречаются в центре правильного 4-многогранника, имеют неравную длину, поскольку они представляют собой четыре характерных радиуса правильного 4-многогранника: радиус вершины, радиус центра ребра, грань радиус центра и радиус центра ячейки. Пять вершин 4-ортосхемы всегда включают в себя одну вершину правильного 4-многогранника, один центр ребра правильного 4-многогранника, один центр грани правильного 4-многогранника, один центр ячейки правильного 4-многогранника и центр правильного 4-многогранника. Эти пять вершин (именно в таком порядке) составляют путь вдоль четырех взаимно перпендикулярных ребер (что делает три поворота под прямым углом), что является характерной особенностью 4-ортосхемы. 4-ортосхема имеет пять различных граней 3-ортосхемы.
↑ Перейти обратно: Перейти обратно: ^а ^б 16-ячеечная структура может быть построена из двух непересекающихся восьмиячеечных колец тремя различными способами; он имеет три ориентации своей пары колец. Каждая ориентация «содержит» отдельную пару изоклинических вращений слева направо, а также пару полностью ортогональных больших квадратов (параллельных слоев Клиффорда), поэтому каждая ориентация представляет собой дискретное расслоение 16-клеток. Каждое восьмиклеточное кольцо содержит три осевые октаграммы, которые имеют разную ориентацию (они обмениваются ролями) в трех дискретных расслоениях и шесть различных изоклинических вращений (три левых и три правых) через клеточные кольца. Три октаграммы (разных цветов) можно увидеть на иллюстрации одного клеточного кольца: одна в роли многоугольника Петри, одна в качестве правой изоклины и одна в качестве левой изоклины. Поскольку каждая октаграмма играет три роли, в 16-ячейке имеется ровно шесть различных изоклин, а не 18.
^ Все пять видов представляют собой одну и ту же ортогональную проекцию 16-ячеечного цилиндра на одну и ту же плоскость (круглое поперечное сечение кольцевого цилиндра с восемью ячейками), если смотреть вдоль центральной оси разрезанного кольцевого цилиндра, изображенного выше, с одного конца цилиндр. Единственная разница состоит в том, какие √ 2 ребра и √ 4 хорды опущены для фокуса. Разные цвета √ 2 ребер кажутся разной длины, поскольку они наклонены к зрителю под разными углами. Вершины пронумерованы от 1 (сверху) до 8 в порядке против часовой стрелки.
↑ Перейти обратно: Перейти обратно: ^а ^б Каждая изоклина имеет восемь хорд √ 2 ребра, а также четыре хорды диаметром √ 4 , которые соединяют каждую четвертую вершину гексаграммы _{8/3} . Антиподальные вершины также имеют соединяющий их скрученный путь из четырех взаимно ортогональных √ 2 ребер. Между противоположными вершинами изоклина плавно изгибается по спирали на протяжении √ 2 хорд своего реберного пути, затрагивая три промежуточные вершины. Каждое ребро √ 2 является ребром большого квадрата, полностью ортогонального другому большому квадрату, в котором хорда √ 4 является диагональю.
↑ Перейти обратно: Перейти обратно: ^а ^б Другой пример левой и правой изоклин вращения, посещающих один и тот же набор вершин, см. в характерном изоклиническом вращении 5-ячейки . Хотя в этих двух особых случаях левая и правая изоклины одного и того же вращения посещают один и тот же набор вершин, они все равно выбирают совершенно разные траектории вращения, поскольку посещают одни и те же вершины в разных последовательностях.
↑ Перейти обратно: Перейти обратно: ^а ^б За исключением 5- и 16-клеточных, ^[С] пара левых и правых изоклинных кругов имеет непересекающиеся вершины: левая и правая спирали изоклин представляют собой непересекающиеся параллели, но вращаются в противоположных направлениях, образуя особый вид двойной спирали, которая не может возникнуть в трех измерениях (где вращающиеся в противоположных направлениях спирали одной и той же радиус должен пересекаться).
↑ Перейти обратно: Перейти обратно: ^а ^б В 16-ячейке каждая отдельная изоклина проходит через все 8 вершин: целое расслоение двух полностью ортогональных больших квадратов. ^[к] 5-клеточный и 16-клеточный — единственные правильные 4-многогранники, в которых каждое дискретное расслоение имеет только один изоклинный слой. ^[аа]
^ Левая и правая изоклины пересекаются в каждой вершине. Это разные последовательности одного и того же набора из 8 вершин. Только относительно набора из 4 пар вершин, которые находятся на расстоянии √ 2 друг от друга, их можно считать клиффордовскими параллельными. Только относительно набора из 4 пар вершин, находящихся на расстоянии √ 4 друг от друга, их можно считать полностью ортогональными. ^[к]
^ В целом это нетипично для изоклинических вращений; обычно левая и правая изоклины не встречаются в одной и той же вершине: существует два непересекающихся набора вершин, достижимых только путем вращения влево или вправо соответственно. ^[аа] Левая и правая изоклины 16-клеточной ячейки образуют особую двойную спираль: необычную не только потому, что она круглая, но и потому, что ее разные левая и правая спирали закручиваются друг вокруг друга через один и тот же набор противоположных вершин. ^[аб] а не через два непересекающихся подмножества антиподальных вершин, как это происходит с парами изоклин в большинстве изоклинических вращений, встречающихся в природе. ^[С] Изоклинические вращения в полностью ортогональных инвариантных плоскостях являются особыми. ^[к] Чтобы понять, как и почему они особенные, визуализируйте две полностью ортогональные инвариантные плоскости вращения, каждая из которых вращается на некоторый угол вращения и наклоняется вбок на тот же угол вращения в совершенно другую плоскость. ^[д] Только когда угол поворота равен 90 °, та другая плоскость, в которой приземляется инвариантная плоскость наклона, сама будет полностью ортогональной инвариантной плоскостью. Целевой плоскостью вращения является полностью ортогональная инвариантная плоскость. Изоклиническое вращение на 90° — единственное вращение, при котором инвариантные плоскости полностью ортогональны друг другу. ^[р] Эта взаимность является причиной того, что и левое, и правое вращения идут в одно и то же место.

Цитаты [ править ]

^ Коксетер 1973 , с. 141, § 7-х. Исторические замечания.
^ Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.5 Сферические группы Кокстера , стр.249
^ Матила Гика, Геометрия искусства и жизни (1977), стр.68
^ Коксетер 1973 , стр. 120=121, § 7.2. рисунок Рис. 7.2 B. См .
^ Coxeter 1973 , стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях; Бесценная таблица, предоставляющая все 20 метрик каждого 4-многогранника в единицах длины ребра. Их необходимо алгебраически преобразовать для сравнения многогранников единичного радиуса.
^ Ким и Роте 2016 , с. 6, § 5. Четырехмерные вращения.
^ Tyrrell & Semple 1971 , стр. 5–6, § 3. Первоначальное определение параллелизма, данное Клиффордом.
^ Kim & Rote 2016 , стр. 7–10, § 6. Углы между двумя плоскостями в 4-пространстве.
^ Kim & Rote 2016 , стр. 8–10, Связь с параллелизмом Клиффорда.
^ Коксетер 1973 , с. 121, § 7.21. См. рисунок Рис. 7.2 B : « $\beta _{4}$ представляет собой четырехмерную дипирамиду, основанную на $\beta _{3}$ (с двумя вершинами в противоположных направлениях по четвёртому измерению)».
^ Тиррелл и Семпл 1971 .
^ Коксетер 1973 , с. 130, § 7.6; «симплициальное подразделение».
^ Коксетер 1973 , стр. 292–293, Таблица I (ii); «16-клеточный, 𝛽 ₄ ».
^ Коксетер 1973 , с. 139, § 7.9 Характеристический симплекс.
^ Коксетер 1973 , с. 290, таблица I(ii); «двугранные углы».
^ Коксетер 1970 , с. 45, Таблица 2: Поворотные соты и их группы; Соты [3,3,4] ₄ — это замощение 3-сферы 2 кольцами из 8 тетраэдрических ячеек.
^ Банчофф 2013 .
^ Коксетер 1973 , стр. 292–293, Таблица I (ii); 24-клеточный h ₁ .
^ Коксетер 1973 , стр. 292–293, Таблица I (ii); 24-клеточный h ₂ .
^ Kim & Rote 2016 , стр. 7–8, § 6 Углы между двумя плоскостями в 4-пространстве; Левая и правая пары изоклинических плоскостей.
^ Коксетер 1973 , с. 293.
^ Коксетер 1991 , стр. 30, 47.
^ Коксетер и Шепард 1992 .
^ Коксетер 1991 , с. 108.
^ Коксетер 1991 , с. 114.

Ссылки [ править ]

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
ХСМ Коксетер :
- Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
- Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Кембридж: Издательство Кембриджского университета.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Калейдоскопы: Избранные сочинения HSM Коксетера | Уайли
  - (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  - (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  - (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Коксетер, HSM ; Шепард, GC (1992). «Портреты семейства сложных многогранников». Леонардо . 25 (3/4): 239–244. дои : 10.2307/1575843 . JSTOR 1575843 . S2CID 124245340 .
- Коксетер, HSM (1970), «Витые соты», Совет конференции серии региональных конференций математических наук по математике , 4 , Провиденс, Род-Айленд: Американское математическое общество
Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 )
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
Ким, Хына; Роте, Гюнтер (2016). «Проверка конгруэнтности наборов точек в 4 измерениях». arXiv : 1603.07269 [ cs.CG ].
Тиррелл, Дж.А.; Семпл, Дж. Г. (1971). Обобщенный параллелизм Клиффорда . Издательство Кембриджского университета . ISBN 0-521-08042-8 .
Банчофф, Томас Ф. (2013). «Разложения тора правильных многогранников в 4-мерном пространстве». В Сенешале, Марджори (ред.). Формирование пространства . Спрингер Нью-Йорк. стр. 257–266 . дои : 10.1007/978-0-387-92714-5_20 . ISBN 978-0-387-92713-8 .

Внешние ссылки [ править ]

Вайсштейн, Эрик В. «16 ячеек» . Математический мир .
Der 16-Zeller (16-клеточные) Правильные многогранники Марко Мёллера в R ⁴ (Немецкий)
Описание и схемы 16-клеточных проекций
Клитцинг, Ричард. «4D однородные многогранники (полихора) x3o3o4o – hex» .

[polytopes_ordered_by_size_and_complexity-6] Выпуклые правильные 4-многогранники можно упорядочить по размеру как мере 4-мерного содержимого (гиперобъема) для того же радиуса. Каждый больший многогранник в последовательности более круглый , чем его предшественник, и содержит больше содержимого. ^[5] в том же радиусе. 4-симплекс (5-ячеечный) — это наименьший случай, а 120-ячеечный — самый большой. Сложность (измеряемая путем сравнения матриц конфигурации или просто количества вершин) следует тому же порядку. Это обеспечивает альтернативную схему числового именования для правильных многогранников, в которой 16-ячеечный является 4-многогранником с 8 точками: вторым в возрастающей последовательности, которая проходит от 4-точечного многогранника с 5 точками до 4-многогранника с 600 точками.

[7] Есть 2 и только 2 16-клетки, вписанные в 8-клетку (тессеракт), 3 и только 3 16-клетки, вписанные в 24-клетку, 75 отдельных 16-клеток (но только 15 непересекающихся 16-клеток), вписанных в 600-ячеечная и 675 отдельных 16-клеточных (но только 75 непересекающихся 16-клеточных), вписанных в 120-ячеечную.

[six_orthogonal_planes_of_the_Cartesian_basis-8] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г В четырехмерном пространстве через точку можно построить 4 перпендикулярные оси и 6 перпендикулярных плоскостей. Без ограничения общности мы можем принять их за оси и ортогональные центральные плоскости декартовой системы координат (w, x, y, z). В 4-х измерениях у нас есть те же 3 ортогональные плоскости (xy, xz, yz), что и в 3-х измерениях, а также еще 3 (wx, wy, wz). Каждая из шести ортогональных плоскостей имеет общую ось с четырьмя другими и противоположна или полностью ортогональна только одной из остальных: единственной, с которой она не имеет общей оси. Таким образом, имеется 3 пары полностью ортогональных плоскостей: xy и wz пересекаются только в начале координат; xz и wy пересекаются только в начале координат; yz и wx пересекаются только в начале координат.

[octahedral_pyramid-9] Перейти обратно: Перейти обратно: ^а ^б ^с Каждая вершина в 16-ячейке является вершиной октаэдрической пирамиды , основанием которой является октаэдр, образованный 6 другими вершинами, с которыми вершина соединена рёбрами. 16-ячеечную структуру можно разобрать (четырьмя различными способами) на две октаэдрические пирамиды, разрезав ее пополам через одну из четырех октаэдрических центральных гиперплоскостей. Если смотреть изнутри на изогнутый трехмерный объем его граничной поверхности из 16 связанных гранями тетраэдров, вершинная фигура 16-ячеечной структуры представляет собой октаэдр. В четырех измерениях вершинный октаэдр на самом деле представляет собой октаэдрическую пирамиду. Вершина октаэдрической пирамиды (вершина, где встречаются шесть ребер) на самом деле не находится в центре октаэдра: она смещена радиально наружу в четвертом измерении, за пределы гиперплоскости, определяемой шестью вершинами октаэдра. 6 ребер вокруг вершины образуют ортогональный трехосный крест в трех измерениях (и в трехмерной проекции четырехмерной пирамиды ), но три линии фактически согнуты на 90 градусов в четвертом измерении, где они встречаются в вершине. .

[10] Граничная поверхность 16-ячейки представляет собой конечное трехмерное пространство, состоящее из 16 тетраэдров, расположенных лицом к лицу (четыре вокруг одного). Это замкнутое, сильно искривленное (неевклидово) трехмерное пространство, внутри которого мы можем двигаться прямо через четыре тетраэдра в любом направлении и вернуться обратно в тот тетраэдр, с которого мы начали. Мы можем визуализировать перемещение внутри этого тетраэдра в джунглях , взбираясь из одного тетраэдра в другой по его 24 стойкам (его краям) и никогда не имея возможности выбраться (или увидеть) из 16 тетраэдров, независимо от того, в каком направлении мы идем (или смотреть). Мы всегда находимся на поверхности 16-клетки (или внутри нее), но никогда внутри самой 16-клетки (ни вне ее). Мы видим, что 6 ребер вокруг каждой вершины расходятся симметрично в трех измерениях и образуют ортогональный трехосный крест, точно так же, как это делают радиусы октаэдра (поэтому мы говорим, что вершинная фигура 16-ячейки - это октаэдр). ^[д]

[completely_orthogonal_planes-11] Перейти обратно: Перейти обратно: ^а ^б ^с Две плоские плоскости A и B евклидова четырехмерного пространства называются полностью ортогональными тогда и только тогда, когда каждая прямая в A ортогональна каждой прямой в B. В этом случае плоскости A и B пересекаются в одной точке O, так что если линия в A пересекается с линией в B, они пересекаются в точке O. A и B перпендикулярны и параллельны Клиффорду . ^[с]

[Clifford_parallel_great_squares-13] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Полностью ортогональные большие квадраты не пересекаются и вращаются независимо, поскольку большие круги, на которых лежат их вершины, параллельны Клиффорду . ^[л] Расстояние между ними составляет √ 2 в каждой паре ближайших вершин (а в 16-клетке все пары, кроме антиподальных, ближайшие). Два квадрата вообще не могут пересекаться, поскольку лежат в плоскостях, пересекающихся только в одной точке: центре 16-клетки. ^[с] Поскольку они перпендикулярны и имеют общий центр, два квадрата, очевидно, не параллельны и разделены обычным способом параллельных квадратов в трех измерениях; скорее они связаны как соседние квадратные звенья в цепи, каждое проходит через другое, не пересекаясь ни в каких точках, образуя звено Хопфа .

[octahedral_hyperplanes-14] Перейти обратно: Перейти обратно: ^а ^б В каждой вершине (и в противоположной ей вершине) 16-ячейки встречаются три больших квадрата. У каждого из них есть отдельный полностью ортогональный квадрат. ^[ф] Таким образом, есть три больших квадрата, полностью ортогональных каждой вершине и противоположной ей вершине (каждой оси). Они образуют октаэдр (центральную гиперплоскость). Каждая осевая линия в 16-ячейке полностью ортогональна гиперплоскости центрального октаэдра, так же как каждая плоскость большого квадрата полностью ортогональна другой плоскости большого квадрата. ^[с] Ось и октаэдр пересекаются только в одной точке (центр 16-ячейки), так как каждая пара полностью ортогональных больших квадратов пересекается только в одной точке (центр 16-ячейки). Каждый центральный октаэдр также является октаэдрической фигурой двух из восьми вершин: двух на его полностью ортогональной оси.

[completely_orthogonal_great_squares-15] Три не полностью вершины ортогональных больших квадрата, которые пересекаются в каждой вершине 16-ячейки, образуют октаэдрическую вершинную фигуру . ^[д] Любые два из них вместе с полностью ортогональным квадратом третьего также образуют октаэдр: центральную октаэдрическую гиперплоскость. ^[час] В 16-ячейке каждая октаэдрическая вершина также является центральной октаэдрической гиперплоскостью.

[vertex_and_central_octahedra-16] Каждая вершина большого квадрата удалена на √ 2 от двух других вершин квадрата и на √ 4 от противоположной вершины. Остальные четыре вершины 16-клетки (также удаленные на √ 2 ) являются вершинами полностью ортогонального квадрата квадрата. ^[г] Каждая вершина из 16 ячеек представляет собой вершину трех пересекающихся ортогональных больших квадратов. У каждого из них есть отдельный полностью ортогональный квадрат. Таким образом, есть три больших квадрата, полностью ортогональных каждой вершине: квадраты, частью которых вершина не является. ^[я]

[completely_orthogonal_Clifford_parallels_are_special-19] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Каждая большая квадратная плоскость изоклинична (параллель Клиффорда) пяти другим квадратным плоскостям, но полностью ортогональна. ^[ф] только одному из них. Каждая пара полностью ортогональных плоскостей имеет параллельные большие круги Клиффорда, но не все параллельные большие круги Клиффорда ортогональны. Есть еще один способ, по которому полностью ортогональные плоскости входят в выдающуюся категорию параллельных плоскостей Клиффорда: они не являются киральными . Пара изоклинических (параллельных Клиффорда) плоскостей является либо левой парой , либо правой парой , если они не разделены двумя углами 90 ° (полностью ортогональные плоскости) или 0 ° (совпадающие плоскости). ^[20] Большинство изоклинических плоскостей соединяются только за счет левого изоклинического вращения или правого изоклинического вращения соответственно. Полностью ортогональные плоскости являются особенными: пара плоскостей представляет собой одновременно левую и правую пару, поэтому либо левое, либо правое изоклиническое вращение объединит их. Поскольку плоскости, разделенные изоклиническим поворотом на 90 °, находятся на расстоянии 180 ° друг от друга, плоскость слева и плоскость справа являются одной и той же плоскостью. ^[р]

[Clifford_parallels-20] Перейти обратно: Перейти обратно: ^а ^б ^с Параллели Клиффорда — это непересекающиеся кривые линии, параллельные в том смысле, что перпендикулярное (кратчайшее) расстояние между ними одинаково в каждой точке. ^[7] Двойная спираль является примером параллелизма Клиффорда в обычном трехмерном евклидовом пространстве. В 4-мерном пространстве параллели Клиффорда представляют собой большие геодезические круги на 3-сфере . ^[8] В 16-ячейке соответствующие вершины полностью ортогональных квадратов большого круга находятся на расстоянии √ 2 друг от друга, поэтому эти квадраты представляют собой параллельные многоугольники Клиффорда. ^[к] Обратите внимание, что только вершины больших квадратов (точки большого круга) находятся на расстоянии √ 2 друг от друга; точки на краях квадратов (на хордах круга) расположены ближе друг к другу.

[long_diagonal_of_the_4-cube-21] Противоположные вершины 4-многогранника единичного радиуса соответствуют противоположным вершинам 8-клеточного гиперкуба (тессеракта). Длинная диагональ этого радиально равностороннего 4-куба равна √ 4 . При изоклиническом вращении на 90° каждая вершина 16-ячейки смещается к своей антиподальной вершине, путешествуя по винтовой геодезической дуге длиной 𝝅 (180°), к вершине √ 4 по длинному диаметру единичного радиуса 4. -многогранник (16-ячеечный или тессеракт), такое же полное смещение, как если бы он был смещен √ 1 четыре раза, путешествуя по пути из четырех последовательных ортогональных ребер тессеракта.

[22] Существует шесть различных путей с двумя ребрами, соединяющих пару противоположных вершин по краям большого квадрата. Левое изоклиническое вращение проходит по диагонали между тремя из них, а правое изоклиническое вращение проходит по диагонали между тремя другими. Эти диагонали представляют собой прямые линии (геодезические), соединяющие противоположные вершины граничных тетраэдрических ячеек в левом восьмиклеточном кольце и правом восьмиклеточном кольце соответственно.

[isocline-23] Перейти обратно: Перейти обратно: ^а ^б ^с В 16-ячейке две антиподальные вершины являются противоположными вершинами двух тетраэдрических ячеек, связанных гранями. Две антиподальные вершины соединены (тремя разными) двуреберными путями большого круга вдоль ребер тетраэдрических ячеек, различными трехреберными путями и четырехреберными путями на изоклинах и многоугольниках Петри. ^[п]

[Möbius_circle-24] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Изоклина — это окружность особого вида, соответствующая паре окружностей Вильярсо, связанных в петлю Мёбиуса . Он проходит через четыре измерения вместо двух. Все обычные круги имеют длину окружности 2𝝅, но изоклина из 16 ячеек представляет собой круг с длиной окружности 4𝝅 (более восьми хорд 90°). Изоклина — это круг, который не лежит на плоскости, но во избежание путаницы мы всегда называем ее изоклиной и оставляем термин «круг» для обычного круга на плоскости.

[isoclinic_rotation-25] Перейти обратно: Перейти обратно: ^а ^б При изоклиническом вращении все 6 ортогональных плоскостей смещаются сразу в двух ортогональных направлениях: они поворачиваются на один и тот же угол и в то же время наклоняются вбок на тот же угол. Изоклиническое смещение (также известное как смещение Клиффорда ) представляет собой четырехмерную диагональ. Точки смещаются на одинаковое расстояние одновременно в четырех ортогональных направлениях и смещаются на общее пифагорово расстояние, равное квадратному корню из четырехкратного квадрата этого расстояния. Все вершины правильного 4-многогранника смещаются в вершину, расположенную на расстоянии не менее двух ребер. Например, когда 16-ячейка с единичным радиусом изоклинически поворачивается на 90 ° в инвариантной плоскости большого квадрата, она также поворачивается на 90 ° в полностью ортогональной инвариантной плоскости большого квадрата. ^[с] Плоскость большого квадрата также наклоняется на 90°, занимая полностью ортогональную плоскость. (В соответствии с изоклинической симметрией каждый большой квадрат вращается на 90 ° и наклоняется на 90 ° в сторону в свою полностью ортогональную плоскость.) Каждая вершина (в каждом большом квадрате) перемещается к своей противоположной вершине на расстояние √ 1 в каждом из четырех ортогональных направлений. , общее расстояние √ 4 . ^[м] Исходная и смещенная вершины находятся на расстоянии двух длин ребра на три. ^[н] разные пути по двум краям большой площади. Но изоклина (спиральная дуга, по которой вершина следует во время изоклинического вращения) не проходит вдоль ребер: она проходит между этими разными путями ребер по диагонали, по геодезической (кратчайшей дуге) между исходной и смещенной вершинами. ^[the] Эта изоклиническая геодезическая дуга не является сегментом обычного большого круга; он не лежит в плоскости какого-либо большого квадрата. Это винтовая дуга 180°, изгибающаяся по окружности сразу в двух совершенно ортогональных плоскостях. Этот круг Мёбиуса не лежит ни в одной плоскости и не пересекает какие-либо вершины между исходной и смещенной вершиной. ^[п]

[exchange_of_completely_orthogonal_planes-27] Перейти обратно: Перейти обратно: ^а ^б ^с Изоклиническое вращение на 90 градусов двух полностью ортогональных плоскостей приводит их друг к другу. При таком вращении жесткой 16-клетки все 6 ортогональных плоскостей поворачиваются на 90 градусов, а также наклоняются вбок на 90 градусов до их полной ортогонализации (параллели Клиффорда). ^[л] самолет. ^[9] Соответствующие вершины двух полностью ортогональных больших квадратов находятся на расстоянии √ 4 (180 °) друг от друга; большие квадраты (параллельные многогранники Клиффорда) находятся на расстоянии √ 4 (180 °) друг от друга; но две полностью ортогональные плоскости находятся на расстоянии 90 ° друг от друга в двух ортогональных углах, которые их разделяют. Если изоклиническое вращение продолжится еще на 90°, каждая вершина завершит поворот на 360°, и каждый большой квадрат вернется в свою исходную плоскость, но в другой ориентации (поменялись оси): он был перевернут «вверх тормашками» на поверхности 16-ячеечный (который теперь «наизнанку»). Продолжение второго изоклинического поворота на 360° (через четыре изоклинических шага 90° на 90°, поворот на 720°) возвращает все в исходное место и ориентацию.

[characteristic_orthoscheme-30] Ортосхема киральный — это неправильный симплекс с прямоугольными гранями , который характерен для некоторого многогранника, если он точно заполняет этот многогранник отражениями себя в своих собственных гранях (его зеркальных стенках ). Каждый правильный многогранник можно разрезать радиально на экземпляры его характерной ортосхемы, окружающей его центр. Характеристическая ортосхема имеет форму, описываемую той же диаграммой Кокстера-Дынкина, что и правильный многогранник без образующего точечного кольца.

[32] Правильный многогранник размерности k имеет характеристическую k -ортосхему, а также характеристическую ( k -1)-ортосхему. Правильный 4-многогранник имеет характерную 5-ячейку (4-ортосхему), на которую он подразделяется своими (3-мерными) гиперплоскостями симметрии, а также характерный тетраэдр (3-ортосхему), на который подразделяется его поверхность (2-мерные) плоскости симметрии ячеек. После разделения его (3-мерной) поверхности на характеристические тетраэдры, окружающие центр каждой ячейки, его (4-мерную) внутреннюю часть можно разделить на характеристические 5-ячейки путем добавления радиусов, соединяющих вершины характеристических тетраэдров поверхности с центром 4-мерного многогранника. ^[12] Образовавшиеся таким образом внутренние тетраэдры и треугольники также будут ортосхемами.

[reversed_greek_symbols-36] Перейти обратно: Перейти обратно: ^а ^б ( Коксетер 1973 ) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы переворачиваем соглашения Кокстера и используем 𝝉 для обозначения характеристического угла.

[characteristic_radii-37] Четыре ребра каждой 4-ортосхемы, которые встречаются в центре правильного 4-многогранника, имеют неравную длину, поскольку они представляют собой четыре характерных радиуса правильного 4-многогранника: радиус вершины, радиус центра ребра, грань радиус центра и радиус центра ячейки. Пять вершин 4-ортосхемы всегда включают в себя одну вершину правильного 4-многогранника, один центр ребра правильного 4-многогранника, один центр грани правильного 4-многогранника, один центр ячейки правильного 4-многогранника и центр правильного 4-многогранника. Эти пять вершин (именно в таком порядке) составляют путь вдоль четырех взаимно перпендикулярных ребер (что делает три поворота под прямым углом), что является характерной особенностью 4-ортосхемы. 4-ортосхема имеет пять различных граней 3-ортосхемы.

[only_one_disjoint_pair_of_eight-cell_rings-40] Перейти обратно: Перейти обратно: ^а ^б 16-ячеечная структура может быть построена из двух непересекающихся восьмиячеечных колец тремя различными способами; он имеет три ориентации своей пары колец. Каждая ориентация «содержит» отдельную пару изоклинических вращений слева направо, а также пару полностью ортогональных больших квадратов (параллельных слоев Клиффорда), поэтому каждая ориентация представляет собой дискретное расслоение 16-клеток. Каждое восьмиклеточное кольцо содержит три осевые октаграммы, которые имеют разную ориентацию (они обмениваются ролями) в трех дискретных расслоениях и шесть различных изоклинических вращений (три левых и три правых) через клеточные кольца. Три октаграммы (разных цветов) можно увидеть на иллюстрации одного клеточного кольца: одна в роли многоугольника Петри, одна в качестве правой изоклины и одна в качестве левой изоклины. Поскольку каждая октаграмма играет три роли, в 16-ячейке имеется ровно шесть различных изоклин, а не 18.

[41] Все пять видов представляют собой одну и ту же ортогональную проекцию 16-ячеечного цилиндра на одну и ту же плоскость (круглое поперечное сечение кольцевого цилиндра с восемью ячейками), если смотреть вдоль центральной оси разрезанного кольцевого цилиндра, изображенного выше, с одного конца цилиндр. Единственная разница состоит в том, какие √ 2 ребра и √ 4 хорды опущены для фокуса. Разные цвета √ 2 ребер кажутся разной длины, поскольку они наклонены к зрителю под разными углами. Вершины пронумерованы от 1 (сверху) до 8 в порядке против часовой стрелки.

[isocline_curve-44] Перейти обратно: Перейти обратно: ^а ^б Каждая изоклина имеет восемь хорд √ 2 ребра, а также четыре хорды диаметром √ 4 , которые соединяют каждую четвертую вершину гексаграммы _{8/3} . Антиподальные вершины также имеют соединяющий их скрученный путь из четырех взаимно ортогональных √ 2 ребер. Между противоположными вершинами изоклина плавно изгибается по спирали на протяжении √ 2 хорд своего реберного пути, затрагивая три промежуточные вершины. Каждое ребро √ 2 является ребром большого квадрата, полностью ортогонального другому большому квадрату, в котором хорда √ 4 является диагональю.

[two_special_cases-45] Перейти обратно: Перейти обратно: ^а ^б Другой пример левой и правой изоклин вращения, посещающих один и тот же набор вершин, см. в характерном изоклиническом вращении 5-ячейки . Хотя в этих двух особых случаях левая и правая изоклины одного и того же вращения посещают один и тот же набор вершин, они все равно выбирают совершенно разные траектории вращения, поскольку посещают одни и те же вершины в разных последовательностях.

[counter-rotating_double_helix-46] Перейти обратно: Перейти обратно: ^а ^б За исключением 5- и 16-клеточных, ^[С] пара левых и правых изоклинных кругов имеет непересекающиеся вершины: левая и правая спирали изоклин представляют собой непересекающиеся параллели, но вращаются в противоположных направлениях, образуя особый вид двойной спирали, которая не может возникнуть в трех измерениях (где вращающиеся в противоположных направлениях спирали одной и той же радиус должен пересекаться).

[each_16-cell_isocline_reaches_all_8_vertices-47] Перейти обратно: Перейти обратно: ^а ^б В 16-ячейке каждая отдельная изоклина проходит через все 8 вершин: целое расслоение двух полностью ортогональных больших квадратов. ^[к] 5-клеточный и 16-клеточный — единственные правильные 4-многогранники, в которых каждое дискретное расслоение имеет только один изоклинный слой. ^[аа]

[48] Левая и правая изоклины пересекаются в каждой вершине. Это разные последовательности одного и того же набора из 8 вершин. Только относительно набора из 4 пар вершин, которые находятся на расстоянии √ 2 друг от друга, их можно считать клиффордовскими параллельными. Только относительно набора из 4 пар вершин, находящихся на расстоянии √ 4 друг от друга, их можно считать полностью ортогональными. ^[к]

[50] В целом это нетипично для изоклинических вращений; обычно левая и правая изоклины не встречаются в одной и той же вершине: существует два непересекающихся набора вершин, достижимых только путем вращения влево или вправо соответственно. ^[аа] Левая и правая изоклины 16-клеточной ячейки образуют особую двойную спираль: необычную не только потому, что она круглая, но и потому, что ее разные левая и правая спирали закручиваются друг вокруг друга через один и тот же набор противоположных вершин. ^[аб] а не через два непересекающихся подмножества антиподальных вершин, как это происходит с парами изоклин в большинстве изоклинических вращений, встречающихся в природе. ^[С] Изоклинические вращения в полностью ортогональных инвариантных плоскостях являются особыми. ^[к] Чтобы понять, как и почему они особенные, визуализируйте две полностью ортогональные инвариантные плоскости вращения, каждая из которых вращается на некоторый угол вращения и наклоняется вбок на тот же угол вращения в совершенно другую плоскость. ^[д] Только когда угол поворота равен 90 °, та другая плоскость, в которой приземляется инвариантная плоскость наклона, сама будет полностью ортогональной инвариантной плоскостью. Целевой плоскостью вращения является полностью ортогональная инвариантная плоскость. Изоклиническое вращение на 90° — единственное вращение, при котором инвариантные плоскости полностью ортогональны друг другу. ^[р] Эта взаимность является причиной того, что и левое, и правое вращения идут в одно и то же место.

[FOOTNOTECoxeter1973141§&nbsp;7-x._Historical_remarks-1] Коксетер 1973 , с. 141, § 7-х. Исторические замечания.

[2] Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.5 Сферические группы Кокстера , стр.249

[3] Матила Гика, Геометрия искусства и жизни (1977), стр.68

[FOOTNOTECoxeter1973120=121§&nbsp;7.2._See_illustration_Fig_7.2<small>B</small>-4] Коксетер 1973 , стр. 120=121, § 7.2. рисунок Рис. 7.2 B. См .

[FOOTNOTECoxeter1973292–293Table_I(ii):_The_sixteen_regular_polytopes_{''p,q,r''}_in_four_dimensions-5] Coxeter 1973 , стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях; Бесценная таблица, предоставляющая все 20 метрик каждого 4-многогранника в единицах длины ребра. Их необходимо алгебраически преобразовать для сравнения многогранников единичного радиуса.

[FOOTNOTEKimRote20166§&nbsp;5._Four-Dimensional_Rotations-12] Ким и Роте 2016 , с. 6, § 5. Четырехмерные вращения.

[FOOTNOTETyrrellSemple19715–6§&nbsp;3._Clifford's_original_definition_of_parallelism-17] Tyrrell & Semple 1971 , стр. 5–6, § 3. Первоначальное определение параллелизма, данное Клиффордом.

[FOOTNOTEKimRote20167–10§&nbsp;6._Angles_between_two_Planes_in_4-Space-18] Kim & Rote 2016 , стр. 7–10, § 6. Углы между двумя плоскостями в 4-пространстве.

[FOOTNOTEKimRote20168–10Relations_to_Clifford_Parallelism-26] Kim & Rote 2016 , стр. 8–10, Связь с параллелизмом Клиффорда.

[FOOTNOTECoxeter1973121§&nbsp;7.21._See_illustration_Fig_7.2<small>B</small>-28] Коксетер 1973 , с. 121, § 7.21. См. рисунок Рис. 7.2 B : « $\beta _{4}$ представляет собой четырехмерную дипирамиду, основанную на $\beta _{3}$ (с двумя вершинами в противоположных направлениях по четвёртому измерению)».

[FOOTNOTETyrrellSemple1971-29] Тиррелл и Семпл 1971 .

[FOOTNOTECoxeter1973130§&nbsp;7.6-31] Коксетер 1973 , с. 130, § 7.6; «симплициальное подразделение».

[FOOTNOTECoxeter1973292–293Table_I(ii);_"16-cell,_𝛽<sub>4</sub>"-33] Коксетер 1973 , стр. 292–293, Таблица I (ii); «16-клеточный, 𝛽 ₄ ».

[FOOTNOTECoxeter1973139§&nbsp;7.9_The_characteristic_simplex-34] Коксетер 1973 , с. 139, § 7.9 Характеристический симплекс.

[FOOTNOTECoxeter1973290Table_I(ii);_"dihedral_angles"-35] Коксетер 1973 , с. 290, таблица I(ii); «двугранные углы».

[FOOTNOTECoxeter197045Table_2:_Reflexible_honeycombs_and_their_groups-38] Коксетер 1970 , с. 45, Таблица 2: Поворотные соты и их группы; Соты [3,3,4] ₄ — это замощение 3-сферы 2 кольцами из 8 тетраэдрических ячеек.

[FOOTNOTEBanchoff2013-39] Банчофф 2013 .

[FOOTNOTECoxeter1973292–293Table_I(ii);_24-cell_''h<sub>1</sub>''-42] Коксетер 1973 , стр. 292–293, Таблица I (ii); 24-клеточный h ₁ .

[FOOTNOTECoxeter1973292–293Table_I(ii);_24-cell_''h<sub>2</sub>''-43] Коксетер 1973 , стр. 292–293, Таблица I (ii); 24-клеточный h ₂ .

[FOOTNOTEKimRote20167–8§&nbsp;6_Angles_between_two_Planes_in_4-Space-49] Kim & Rote 2016 , стр. 7–8, § 6 Углы между двумя плоскостями в 4-пространстве; Левая и правая пары изоклинических плоскостей.

[FOOTNOTECoxeter1973293-51] Коксетер 1973 , с. 293.

[FOOTNOTECoxeter199130,_47-52] Коксетер 1991 , стр. 30, 47.

[FOOTNOTECoxeterShephard1992-53] Коксетер и Шепард 1992 .

[FOOTNOTECoxeter1991108-54] Коксетер 1991 , с. 108.

[FOOTNOTECoxeter1991114-55] Коксетер 1991 , с. 114.

[1]

[2]

[3]

[4]

[а]

[б]

[с]

[и]

[ф]

[д]

[6]

[Дж]

[г]

[д]

[р]

[10]

[час]

[л]

[11]

[с]

[т]

[13]

[14]

[15]

[в]

[v]

[the]

[16]

[17]

[п]

[В]

[х]

[18]

[19]

[и]

[аб]

[и]

[объявление]

[21]

[22]

[23]

[24]

[25]

[5]

[я]

[20]

[7]

[8]

[к]

[м]

[н]

[9]

[12]

[С]

[аа]