Гиперпрямоугольник

Гиперпрямоугольник Ортотоп
Прямоугольный кубоид представляет собой 3-ортотоп.
Тип	Призма
Лица	22н
Края	п × 2 п -1
Вершины	2 н
Символ Шлефли	{}×{}×···×{} = {} н
Диаграмма Кокстера	···
Группа симметрии	[2 п -1 ] , порядок 2 н
Двойной многогранник	Прямоугольная н- винтовка
Характеристики	выпуклый , зоноэдр , изогональный

В геометрии гиперпрямоугольник . (также называемый параллелепипедом , гипербоксом или ортотопом) ), является обобщением прямоугольника ( плоской фигуры ) и прямоугольного кубоида ( сплошной фигуры ) на более высокие измерения .Необходимым и достаточным условием является то, что оно конгруэнтно произведению декартову конечных интервалов . Если все ребра одинаковой длины, это гиперкуб .Гиперпрямоугольник — частный случай параллелоэдра .

Типы

Четырехмерный ортотоп, скорее всего, представляет собой гиперкубоид.

Частным случаем n -мерного ортотопа, где все ребра имеют одинаковую длину, является n - куб или гиперкуб.

По аналогии, термин «гиперпрямоугольник» может относиться к декартовым произведениям ортогональных интервалов других видов, таких как диапазоны ключей в теории баз данных или диапазоны целых чисел , а не действительных чисел .

Двойной многогранник

н- пистолет
Пример: 3 пистолета
Тип	Призма
Лица	22н
Вершины	2 н
Символ Шлефли	{}+{}+···+{} = n {}
Диаграмма Кокстера	...
Группа симметрии	[2 п -1 ] , порядок 2 н
Двойной многогранник	n- ортотоп
Характеристики	выпуклый , изотопический

Двойственный многогранник - ортотопа n по-разному называли прямоугольным n - ортоплексом , ромбическим n - фусилем или n - ромбовидным . Он строится по 2 n точкам, расположенным в центре прямоугольных граней ортотопа.

быть может n -фузиля Символ Шлефли представлен суммой n ортогональных отрезков: { } + { } + ... + { } или n { }.

1-фузиль — это отрезок прямой . 2-фузиль — это ромб . Его плоские поперечные выделения по всем парам осей являются ромбами .

н	Пример изображения
1	Отрезок линии { }
2	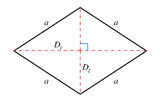Ромб { } + { } = 2{ }
3	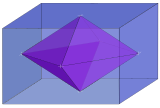Ромбический 3-ортоплекс внутри 3-ортотопа { } + { } + { } = 3{ }

См. также

• Минимальный ограничивающий прямоугольник
• Кубовидный

Ссылки

• Коксетер, Гарольд Скотт Макдональд (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр. стр. 122–123 . ISBN  0-486-61480-8 .

Внешние ссылки

• Вайсштейн, Эрик В. «Ортотоп» . Математический мир .