Шестимерное пространство

«Шестое измерение» перенаправляется сюда. Чтобы узнать о других значениях, см. «Шестое измерение» .

Шестимерное пространство — это любое пространство, имеющее шесть измерений, шесть степеней свободы и требующее шесть фрагментов данных или координат для указания местоположения в этом пространстве. Их бесконечное множество, но наибольший интерес представляют более простые модели, моделирующие некоторые аспекты окружающей среды. Особый интерес представляет шестимерное евклидово пространство , в котором построены 6-многогранники и 5-сфера. шестимерное эллиптическое пространство и гиперболические пространства Также изучаются с постоянной положительной и отрицательной кривизной.

Формально шестимерное евклидово пространство, $\mathbb {R} ^{6}$, генерируется путем рассмотрения всех действительных 6- кортежей как 6- векторов в этом пространстве. Как таковое оно обладает свойствами всех евклидовых пространств, поэтому оно линейно, имеет метрику и полный набор векторных операций. В частности, скалярное произведение между двумя 6-векторами легко определяется и может использоваться для вычисления метрики. 6 × 6 Матрицы можно использовать для описания преобразований, таких как повороты , которые сохраняют начало координат фиксированным.

В более общем смысле любое пространство, которое можно локально описать шестью координатами (не обязательно евклидовыми), является шестимерным. Одним из примеров является поверхность 6-сферы S. ⁶ . Это совокупность всех точек семимерного пространства (евклидова). $\mathbb {R} ^{7}$которые находятся на фиксированном расстоянии от начала координат. Это ограничение уменьшает количество координат, необходимых для описания точки на шестимерной сфере, на одну, поэтому она имеет шесть измерений. Такие неевклидовы пространства встречаются гораздо чаще, чем евклидовы, и в шести измерениях они имеют гораздо больше приложений.

Геометрия

6-многогранник

Основная статья: 6-многогранник

называется Шестимерный многогранник 6-мерным многогранником. Наиболее изученными являются правильные многогранники , которых в шести измерениях всего три : 6-симплекс , 6-куб и 6-ортоплекс . Более широкое семейство — это однородные 6-многогранники , построенные из фундаментальных областей симметрии отражения, каждая из которых определяется группой Коксетера . Каждый однородный многогранник определяется кольцевой диаграммой Кокстера–Дынкина . 6 -демикуб — ​​уникальный многогранник из семейства D ₆ , а также 2 ₂₁ и 1 ₂₂ многогранники из семейства E ₆ .

Однородные многогранники в шести измерениях
(Отображается в виде ортогональных проекций в каждой плоскости симметрии Кокстера)

А 6	Б 6		DД6	EЕ6
6-симплекс {3,3,3,3,3}	6-куб. {4,3,3,3,3}	6-ортоплекс {3,3,3,3,4}	6-демикуб = {3,3 3,1 } = ч{4,3,3,3,3}	2 21 = {3,3,3 2,1 }	1 22 = {3,3 2,2 }

5-сфера

Пятимерная сфера, или шестимерная гиперсфера, представляет собой пятимерную поверхность, равноудалённую от точки. Имеет символ S ⁵ , а уравнение для 5-сферы радиуса r , центр начала координат

$S^{5}=\left\{x\in \mathbb {R} ^{6}:\|x\|=r\right\}.$

Объем шестимерного пространства, ограниченного этой 5-сферой, равен

$V_{6}={\frac {\pi ^{3}r^{6}}{6}}$

что составляет 5,16771 × r ⁶ , или 0,0807 наименьшего 6-куба , содержащего 5-сферу.

6-сфера

Шестимерная сфера, или семимерная гиперсфера, представляет собой шестимерную поверхность, равноудалённую от точки. Имеет символ S ⁶ , а уравнение для 6-сферы радиуса r , центр начала координат

$S^{6}=\left\{x\in \mathbb {R} ^{7}:\|x\|=r\right\}.$

Объем пространства, ограниченного этой 6-сферой, равен

$V_{7}={\frac {16\pi ^{3}r^{7}}{105}}$

что составляет 4,72477 × r ⁷ , или 0,0369 наименьшего 7-куба , содержащего 6-сферу.

Приложения

Трансформации в трех измерениях

В трехмерном пространстве жесткое преобразование имеет шесть степеней свободы , три перемещения по трем координатным осям и три по группе вращения SO(3) . Часто эти преобразования обрабатываются отдельно, поскольку они имеют очень разные геометрические структуры, но существуют способы справиться с ними, рассматривая их как один шестимерный объект.

Теория винта

Основная статья: Теория винта

В теории винта угловая и линейная скорости объединены в один шестимерный объект, называемый твистом . Подобный объект, называемый гаечным ключом , сочетает в себе силы и крутящие моменты в шести измерениях. Их можно рассматривать как шестимерные векторы, которые линейно преобразуются при изменении системы отсчета. Переводы и повороты не могут быть выполнены таким образом, но связаны с поворотом возведением в степень .

Фазовое пространство

Основная статья: Фазовое пространство

Фазовый портрет генератора Ван дер Поля

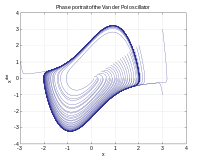
Фазовое пространство — это пространство, состоящее из положения и импульса частицы, которые можно изобразить вместе на фазовой диаграмме , чтобы подчеркнуть взаимосвязь между величинами. Обычная частица, движущаяся в трех измерениях, имеет фазовое пространство с шестью измерениями, их слишком много, чтобы их можно было построить, но их можно проанализировать математически.

Вращения в четырех измерениях

Основная статья: Вращения в 4-мерном евклидовом пространстве

Группа вращения в четырех измерениях, SO(4), имеет шесть степеней свободы. В этом можно убедиться, рассмотрев матрицу 4 × 4, которая представляет вращение: поскольку это ортогональная матрица, матрица определяется, с точностью до изменения знака, например, шестью элементами над главной диагональю. Но эта группа не является линейной и имеет более сложную структуру, чем другие приложения, замеченные до сих пор.

Другой способ взглянуть на эту группу — умножение кватернионов . Каждое вращение в четырех измерениях может быть достигнуто путем умножения на пару единичных кватернионов , один до и один после вектора. Эти кватернионы уникальны, с точностью до смены знака для них обоих, и при таком использовании генерируют все вращения, поэтому произведение их групп S ³ × С ³ , является двойным покрытием SO(4), которое должно иметь шесть измерений.

Хотя пространство, в котором мы живем, считается трехмерным, четырехмерное пространство имеет практическое применение. Кватернионы, один из способов описания трехмерного вращения, состоят из четырехмерного пространства. Вращения между кватернионами, например, для интерполяции, происходят в четырех измерениях. Пространство-время , имеющее три пространственных измерения и одно временное измерение, также является четырехмерным, хотя и имеет структуру, отличную от евклидова пространства .

Электромагнетизм

В электромагнетизме электромагнитное поле обычно рассматривается как состоящее из двух частей: электрического поля и магнитного поля . Оба они представляют собой трехмерные векторные поля , связанные друг с другом уравнениями Максвелла . Второй подход состоит в том, чтобы объединить их в один объект, шестимерный электромагнитный тензор , тензорное или бивекторное представление электромагнитного поля. Используя это, уравнения Максвелла можно объединить из четырех уравнений в одно особенно компактное одно уравнение:

$\partial \mathbf {F} =\mathbf {J} \,$

где F — бивекторная форма электромагнитного тензора, J — четырехток и ∂ — подходящий дифференциальный оператор .

Теория струн

Многообразие Калаби – Яу ( 3D-проекция )

В физике теория струн — это попытка описать общую теорию относительности и квантовую механику с помощью единой математической модели. Хотя это попытка смоделировать нашу Вселенную, она происходит в пространстве с большим количеством измерений, чем четыре привычных нам пространства-времени. В частности, ряд теорий струн действуют в десятимерном пространстве, добавляя дополнительные шесть измерений. Эти дополнительные измерения требуются теорией, но, поскольку их нельзя наблюдать, они считаются совершенно другими, возможно, компактизированными , чтобы сформировать шестимерное пространство с определенной геометрией, слишком маленькой, чтобы ее можно было наблюдать.

С 1997 года появилась еще одна теория струн, работающая в шести измерениях. Маленькие теории струн — это негравитационные теории струн в пяти и шести измерениях, возникающие при рассмотрении пределов десятимерной теории струн.

Теоретическая основа

Бивекторы в четырёх измерениях

Ряд вышеупомянутых приложений можно алгебраически связать друг с другом, рассматривая действительные шестимерные бивекторы в четырех измерениях. Они могут быть написаны $\Lambda ^{2}\mathbb {R} ^{4}$ для множества бивекторов в евклидовом пространстве или $\Lambda ^{2}\mathbb {R} ^{3,1}$для множества бивекторов в пространстве-времени. Координаты Плюкера являются бивекторами в $\mathbb {R} ^{4}$ в то время как электромагнитный тензор, обсуждавшийся в предыдущем разделе, является бивектором в $\mathbb {R} ^{3,1}$. Бивекторы можно использовать для генерации вращений в любом $\mathbb {R} ^{4}$ или $\mathbb {R} ^{3,1}$ через экспоненциальную карту (например, применяя экспоненциальную карту всех бивекторов в $\Lambda ^{2}\mathbb {R} ^{4}$ генерирует все вращения в $\mathbb {R} ^{4}$). Их также можно связать с общими преобразованиями в трех измерениях через однородные координаты, которые можно рассматривать как модифицированные вращения в пространстве. $\mathbb {R} ^{4}$.

Бивекторы возникают из сумм всех возможных клиновых произведений между парами 4-векторов. Поэтому они имеют C 4
2   = 6 компонентов, и в наиболее общем виде его можно записать как

$\mathbf {B} =B_{12}\mathbf {e} _{12}+B_{13}\mathbf {e} _{13}+B_{14}\mathbf {e} _{14}+B_{23}\mathbf {e} _{23}+B_{24}\mathbf {e} _{24}+B_{34}\mathbf {e} _{34}$

Это первые бивекторы, которые не могут быть порождены произведениями пар векторов. Те, которые могут это сделать, — это простые бивекторы , а вращения, которые они генерируют, — это простые вращения . Другие вращения в четырех измерениях представляют собой двойные и изоклинические вращения и соответствуют непростым бивекторам, которые не могут быть созданы с помощью одного клинового произведения.

6-векторы

6-векторы — это просто векторы шестимерного евклидова пространства. Как и другие подобные векторы, они линейны , их можно складывать, вычитать и масштабировать, как и в других измерениях. Вместо использования букв алфавита в более высоких измерениях для обозначения измерений обычно используются суффиксы, поэтому общий шестимерный вектор можно записать a = (a ₁ , a ₂ , a ₃ , a ₄ , a ₅ , a ₆ ) . Записанные таким образом, шесть базисных векторов : (1, 0, 0, 0, 0, 0) , (0, 1, 0, 0, 0, 0) , (0, 0, 1, 0, 0, 0) , (0, 0, 0, 1, 0, 0) , (0, 0, 0, 0, 1, 0) и (0, 0, 0, 0, 0, 1) .

Из векторных операторов векторное произведение нельзя использовать в шести измерениях; вместо этого произведение клина двух 6-векторов дает бивектор с 15 измерениями. Скалярное произведение двух векторов равно

$\mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+a_{4}b_{4}+a_{5}b_{5}+a_{6}b_{6}.$

Его можно использовать для нахождения угла между двумя векторами и нормой .

$\left|\mathbf {a} \right\vert ={\sqrt {\mathbf {a} \cdot \mathbf {a} }}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}+{a_{4}}^{2}+{a_{5}}^{2}+{a_{6}}^{2}}}.$

Это можно использовать, например, для вычисления диагонали 6-куба ; с одним углом в начале координат, краями, выровненными по осям и длиной стороны 1, противоположный угол может находиться в точке (1, 1, 1, 1, 1, 1) , норма которого равна

${\sqrt {1+1+1+1+1+1}}={\sqrt {6}}=2.4495,$

что является длиной вектора и, следовательно, диагонали 6-куба.

Бивекторы Гиббса

В 1901 году Дж. Гиббс опубликовал работу о векторах, включающую шестимерную величину, которую он назвал бивектором . Он состоял из двух трехмерных векторов в одном объекте, который он использовал для описания эллипсов в трех измерениях. Он вышел из употребления по мере развития других методов, и теперь название бивектор более тесно связано с геометрической алгеброй.

Ссылки

• Лунесто, Пертти (2001). Алгебры Клиффорда и спиноры . Кембридж: Издательство Кембриджского университета . ISBN  978-0-521-00551-7 .

• Ахарони, Офер (2000). «Краткий обзор «маленьких теорий струн» ». Классическая и квантовая гравитация . 17 (5). arXiv : hep-th/9911147 . Бибкод : 2000CQGra..17..929A . дои : 10.1088/0264-9381/17/5/302 .