Возведение в степень

$б н$
б н
обозначение
	основание b и показатель степени n

Графики $y = b Икс$ для различных баз $b$ : основание $10$ , база $и$ , база $2$ , база $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2 $ . Каждая кривая проходит через точку $(0, 1),$ поскольку любое ненулевое число, возведенное в степень $0,$ равно $1$ . При $x = 1$ значение $y$ равно основанию, поскольку любое число, возведенное в степень $1,$ является самим числом.

В математике , возведение в степень — это операция включающая два числа : основание и показатель степени или степень . Возведение в степень записывается как $b н$ , где $b$ — основание , а $n$ — степень ; это произносится как « $b$ (возведенный) в (степень) $n$ ». ^[1] Когда $n$ — положительное целое число , возведение в степень соответствует повторному умножению основания: то есть $b н$ является продуктом умножения $n$ оснований: ^[1]

b^{n}=\underbrace {b\times b\times \dots \times b\times b} _{n{\text{ times}}}.

Показатель степени обычно отображается в виде верхнего индекса справа от основания. В этом случае $б н$ называется « b в n- й степени», « b степень (возведенный) в n-ю », « в n- й степени b », « b в n- ю степень», ^[2] или наиболее кратко как « б к н (ому)».

Исходя из изложенного выше основного факта, что для любого положительного целого числа $n$ , $b^{n}$ является $n$ случаи $b$ все умножаются друг на друга, из чего непосредственно следуют некоторые другие свойства возведения в степень. В частности: ^{[номер 1]}

{\begin{aligned}b^{n+m}&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=b^{n}\times b^{m}\end{aligned}}

Другими словами, при умножении основания, возведенного в одну степень, на то же самое основание, возведенное в другую степень, показатели степени складываются. Из этого основного правила, которое добавляют показатели, мы можем вывести, что $b^{0}$ должно быть равно 1 для любого $b\neq 0$ , следующее. Для любого $n$ , $b^{0}\times b^{n}=b^{0+n}=b^{n}$ . Разделив обе части на $b^{n}$ дает $b^{0}=b^{n}/b^{n}=1$ .

Дело в том, что $b^{1}=b$ можно аналогичным образом вывести из того же правила. Например, $(b^{1})^{3}=b^{1}\times b^{1}\times b^{1}=b^{1+1+1}=b^{3}$ . Извлечение кубического корня из обеих частей дает $b^{1}=b$ .

Правило, согласно которому при умножении показатели суммируются, также можно использовать для получения свойств отрицательных целочисленных показателей. Рассмотрим вопрос о том, что $b^{-1}$ должно означать. Чтобы соблюдать правило «добавления показателей», должно быть так, что $b^{-1}\times b^{1}=b^{-1+1}=b^{0}=1$ . Разделив обе части на $b^{1}$ дает $b^{-1}=1/b^{1}$ , что проще записать как $b^{-1}=1/b$ , используя результат выше, который $b^{1}=b$ . По аналогичному аргументу, $b^{-n}=1/b^{n}$ .

Из этого же правила следуют и свойства дробных показателей. Например, предположим, что мы рассматриваем ${\sqrt {b}}$ и спросим, существует ли какой-нибудь подходящий показатель степени, который мы можем назвать $r$ , такой, что $b^{r}={\sqrt {b}}$ . Из определения квадратного корня мы имеем, что ${\sqrt {b}}\times {\sqrt {b}}=b$ . Следовательно, показатель $r$ должно быть таким, что $b^{r}\times b^{r}=b$ . Используя тот факт, что умножение приводит к сложению показателей, дает $b^{r+r}=b$ . $b$ в правой части также можно записать как $b^{1}$ , давая $b^{r+r}=b^{1}$ . Приравнивая показатели обеих частей, имеем $r+r=1$ . Поэтому, $r={\frac {1}{2}}$ , так ${\sqrt {b}}=b^{1/2}$ .

Определение возведения в степень можно расширить, чтобы разрешить любой действительный или комплексный показатель. Возведение в степень целочисленными показателями также может быть определено для широкого спектра алгебраических структур, включая матрицы .

Возведение в степень широко используется во многих областях, включая экономику , биологию , химию , физику и информатику , с такими приложениями, как сложные проценты , рост населения , кинетика химических реакций , волновое поведение и криптография с открытым ключом .

Этимология [ править ]

Термин « экспонента» происходит от латинского expontem , причастия настоящего времени от exponere , что означает «выдвигать». ^[3] Термин власть ( лат . potentia, potestas, dignitas ) является неправильным переводом. ^[4]^[5] древнегреческого , здесь: « δύναμις ( dúnamis усиление» ^[4]), используемый греческим математиком Евклидом для обозначения квадрата прямой, ^[6] вслед за Гиппократом Хиосским . ^[7]

История [ править ]

Античность [ править ]

Счетчик песка [ править ]

В «Счетчике песка» Архимед доказал закон экспоненты, $10 а \cdot 10 б = 10 а + б$ , необходимые для манипулирования степенями $10$ . ^[8] Затем он использовал степень $10$ , чтобы оценить количество песчинок, которые могут содержаться во Вселенной.

ислама век Золотой

Мал и Кааба («квадрат» и «куб») [ править ]

В IX веке персидский математик Аль-Хорезми использовал термины مَال ( māl , «имущество», «собственность») для обозначения квадрата — мусульмане, «как и большинство математиков того и более раннего времени, думали о квадрате числа как о изображение местности, особенно земли, следовательно, собственности» ^[9]- и كَعْبَة ( Кааба , «куб») для куба , который позже исламские математики представили в математических обозначениях как буквы мим (м) и каф (к) соответственно, к 15 веку, как видно из работы Абу' л-Хасан ибн Али аль-Каласади . ^[10]

15–18 века [ править ]

Знакомство с показателями [ править ]

Николя Шуке использовал форму экспоненциальной записи в 15 веке, например $122$ представлять $12 х 2$ . ^[11]Позже это использовалось Хенриком Грамматеусом и Майклом Стифелем в 16 веке. В конце 16 века Йост Бюрги использовал римские цифры для показателей степени, аналогично тому, как это делал Шюке, например, iii 4 для $4 x. 3$ . ^[12]

«Экспонента»; «квадрат» и «куб» [ править ]

Слово экспонента было придумано в 1544 году Майклом Стифелем. ^[13]^[14] В 16 веке Роберт Рекорд использовал термины «квадрат», «куб», «зензизензический» ( четвертая степень ), «сурсолид» (пятый), «зензикуб» (шестой), «второй сурсолид» (седьмой) и «зензизензизензический» (восьмой). ^[9] Биквадрат также использовался для обозначения четвертой степени.

экспоненциальная запись Современная

В 1636 году Джеймс Юм использовал, по существу, современную систему обозначений, когда в «Алгебре Вьете» он написал $А. III$ для $ 3$ . ^[15]В начале 17 века первая форма нашей современной экспоненциальной записи была введена Рене Декартом в его тексте под названием «Геометрия» ; там обозначения введены в I книге. ^[16]

Я обозначаю... $аа$ , или $а 2$ при умножении $a$ на себя; и $ 3$ умножив его еще раз на $a$ и, таким образом, до бесконечности.
— Рене Декарт, Геометрия

Некоторые математики (например, Декарт) использовали показатели степени только для степеней больше двух, предпочитая представлять квадраты как многократное умножение. Таким образом, они будут писать многочлены , например, как $ax + bxx + cx. 3 + д$ .

«Индексы» [ править ]

Сэмюэл Джик ввел термин « индексы» в 1696 году. ^[6] Термин «инволюция» использовался как синоним термина « индексы» , но его использование сократилось. ^[17] и его не следует путать с его более общим значением .

Переменные показатели степени, нецелые показатели степени [ править ]

В 1748 году Леонард Эйлер ввел переменные показатели степени и, косвенно, нецелые показатели степени, написав:

Рассмотрим экспоненты или степени, в которых показатель степени сам является переменной. Ясно, что величины такого рода не являются алгебраическими функциями , так как в них показатели степени должны быть постоянными. ^[18]

Терминология [ править ]

Выражение $б 2 = b \cdot b$ называется « квадратом b $»$ или « $b$ в квадрате», поскольку площадь квадрата со стороной $b$ равна $b. 2$ . (Это правда, что его также можно было бы назвать « $b$ во второй степени», но «квадрат $b$ » и « $b$ в квадрате» настолько укоренились в традициях и удобствах, что « $b$ во второй степени» имеет тенденцию звучать необычно или неуклюжий.)

Аналогично, выражение $b 3 = b \cdot b \cdot b$ называется « кубом b $»$ или « $b$ в кубе», поскольку объем куба с длиной стороны $b$ равен $b. 3$ .

Когда показатель степени является положительным целым числом , он указывает, сколько копий основания умножается вместе. Например, $35 = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = 243$ . Основание $3$ появляется $5$ при умножении $раз, поскольку показатель степени равен 5$ . Здесь $243$ — это 5-я степень числа 3 или 3, возведенная в 5-ю степень .

Слово «поднятый» обычно опускается, а иногда и «власть», поэтому $35$ можно просто прочитать «3 к 5» или «3 к 5». Следовательно, возведение в степень $b н$ может быть выражено как « b в степени n », « b в n -й степени», « b в n-й степени» или, наиболее кратко, как « b в n ».

Целочисленные показатели [ править ]

Операцию возведения в степень с целочисленными показателями можно определить непосредственно из элементарных арифметических операций .

Положительные показатели [ править ]

Определение возведения в степень как повторного умножения можно формализовать с помощью индукции . ^[19] и это определение можно использовать, как только появится ассоциативное умножение:

Базовый случай

b^{1}=b

и повторение

b^{n+1}=b^{n}\cdot b.

Ассоциативность умножения означает, что для любых натуральных чисел $m$ и $n$ ,

b^{m+n}=b^{m}\cdot b^{n},

и

(b^{m})^{n}=b^{mn}.

Нулевой показатель [ править ]

Как упоминалось ранее, (ненулевое) число, возведенное в $степень 0$ , равно $1$ : ^[20]^[1]

b^{0}=1.

Это значение также получается с помощью соглашения о пустом произведении , которое можно использовать в каждой алгебраической структуре с умножением, имеющим единицу . Таким образом, формула

b^{m+n}=b^{m}\cdot b^{n}

также справедливо для $n=0$ .

Случай $00$ является спорным. В контекстах, где рассматриваются только целые степени, значению $1$ обычно присваивается $0. 0$ но в противном случае выбор того, присвоить ли ему значение и какое значение присвоить, может зависеть от контекста. Дополнительные сведения см. в разделе Ноль в степени нуля .

Отрицательные показатели [ править ]

Возведение в степень с отрицательными показателями определяется следующим тождеством, которое справедливо для любого целого числа $n$ и ненулевого $b$ :

b^{-n}={\frac {1}{b^{n}}}

. ^[1]

Возведение 0 в отрицательную степень не определено, но в некоторых случаях это можно интерпретировать как бесконечность ( $\infty$ ). ^[21]

Это определение возведения в степень с отрицательными показателями является единственным, которое позволяет расширить тождество. $b^{m+n}=b^{m}\cdot b^{n}$ к отрицательным показателям (рассмотрим случай $m=-n$ ).

То же самое определение применимо и к обратимым элементам в мультипликативном моноиде , то есть алгебраической структуре , с ассоциативным умножением и мультипликативным тождеством, обозначаемым $1$ (например, квадратные матрицы заданной размерности). В частности, в такой структуре обратный обратимому элементу $x$ стандартно обозначается $x^{-1}.$

Личности и свойства [ править ]

Следующие личности , часто называемые Правила экспоненты действуют для всех целочисленных экспонент при условии, что основание не равно нулю: ^[1]

{\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}

В отличие от сложения и умножения, возведение в степень не является коммутативным . Например, $23 = 8 \neq 3 2 = 9$ . Кроме того, в отличие от сложения и умножения, возведение в степень не является ассоциативным . Например, $(2 3) 2 = 8 2 = 64$ , тогда как $2 (3 2) = 2 9 = 512$ . Без круглых скобок обычный порядок операций в последовательного возведения степень в надстрочной нотации - сверху вниз (или правоассоциативный ), а не снизу вверх. ^[22]^[23]^[24](или левоассоциативный ). То есть,

b^{p^{q}}=b^{\left(p^{q}\right)},

что в целом отличается от

\left(b^{p}\right)^{q}=b^{pq}.

Степени суммы [ править ]

Степени суммы обычно можно вычислить по степеням слагаемых по биномиальной формуле

(a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.

Однако эта формула верна только в том случае, если слагаемые коммутируют (т. е. $ab = ba$ ), что подразумевается, если они принадлежат структуре коммутативной к . В противном случае, если $a$ и $b$ — скажем, квадратные матрицы одинакового размера, эту формулу использовать нельзя. Отсюда следует, что в компьютерной алгебре многие алгоритмы , включающие целочисленные показатели степени, должны быть изменены, когда основания возведения в степень не коммутируют. Некоторые системы компьютерной алгебры общего назначения используют другое обозначение (иногда $^^$ вместо $^$ ) для возведения в степень с некоммутативными основаниями, которое затем называется некоммутативным возведением в степень .

Комбинаторная интерпретация

Для неотрицательных целых чисел $n$ и $m$ значение $n м$ — это количество функций от набора из $m$ элементов до набора из $n$ элементов (см. кардинальное возведение в степень ). Такие функции можно представить в виде $m$ - кортежей из $n$ -элементного множества (или в виде $m$ -буквенных слов из $n$ -буквенного алфавита). Некоторые примеры конкретных значений $m$ и $n$ приведены в следующей таблице:

$н м$	Затем $ м$ возможных $m$ -кортежей элементов из множества ${1, ..., n}$
0 ⁵ = 0	никто
1 ⁴ = 1	(1, 1, 1, 1)
2 ³ = 8	(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)
3 ² = 9	(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)
4 ¹ = 4	(1), (2), (3), (4)
5 ⁰ = 1	()

Особые базы [ править ]

Степени десяти [ править ]

В десятичной , системе счисления целые степени $10$ записываются как цифра $1$ за которой или перед которой следует количество нулей, определяемое знаком и величиной показателя степени. Например, $103 = 1000$ и $10 -4 = 0.0001$ .

Возведение в степень с основанием $10$ используется в научной записи для обозначения больших или малых чисел. Например, 299 792 458 м/с ( скорость света в вакууме, в метрах в секунду ) можно записать как 2,997 924 58 × 10. ⁸ м/с , а затем аппроксимируется как 2,998 × 10 ⁸ РС .

Префиксы СИ, основанные на степени $10,$ также используются для описания малых или больших величин. Например, приставка килограмм означает $10. 3 = 1000$ , значит километр равен 1000 м .

Степени двойки [ править ]

Первые отрицательные степени $двойки$ обычно используются и имеют специальные названия, например: половина и четверть .

Степени $двойки$ появляются в теории множеств , поскольку множество из $n$ членов имеет набор степеней , набор всех его подмножеств , который имеет $2 н$ члены.

Целые степени $2$ важны в информатике . Целые положительные степени $2 н$ указать количество возможных значений $n$ - битного целого двоичного числа ; например, байт может занимать $28 = 256$ различных значений. Двоичная система счисления выражает любое число как сумму степеней $2$ и обозначает его как последовательность $0$ и $1$ , разделенных двоичной точкой , где $1$ указывает степень $2$ , которая появляется в сумме; показатель степени определяется местом этой $1$ : неотрицательные показатели степени представляют собой ранг единицы $слева$ от точки (начиная с $0$ ), а отрицательные показатели степени определяются рангом справа от точки.

Полномочия одного [ править ]

Каждая степень единицы равна: $1 н = 1$ . Это верно, даже если $n$ отрицательно.

Первая степень числа — это само число: $n 1 = п$ .

Степени нуля [ править ]

Если показатель степени $n$ положителен ( $n > 0$ ), $n-$ я степень нуля равна нулю: $0 н = 0$ .

Если показатель степени $n$ отрицателен ( $n < 0$ ), $n-$ я степень нуля равна $0. н$ не определено, поскольку оно должно равняться $1/0^{-n}$ с $- n > 0$ , и это будет $1/0$ согласно вышеизложенному.

Выражение $00$ либо определяется как $1$ , либо остается неопределенным.

Полномочия отрицательного [ править ]

Если $n$ — четное целое число, то $(-1) н = 1$ . Это связано с тем, что отрицательное число, умноженное на другое отрицательное число, отменяет знак и, таким образом, дает положительное число.

Если $n$ — нечетное целое число, то $(-1) н = -1$ . останется $-1$ Это связано с тем, что после удаления $пар -1$ .

По этой причине степени $-1$ полезны для выражения чередующихся последовательностей . Аналогичное обсуждение степеней комплексного числа $i$ см. в § корнях комплексного числа n-й степени .

Большие показатели [ править ]

Предел последовательности степеней числа, большего единицы, расходится; другими словами, последовательность растет неограниченно:

б н \to \infty

при

n \to \infty,

когда

b > 1

Это можно прочитать как « b в степени n стремится к +∞, поскольку n стремится к бесконечности, когда b больше единицы».

Степени числа с абсолютным значением меньше единицы стремятся к нулю:

б н \to 0

при

n \to \infty,

когда

| б | < 1

Любая сила единицы всегда одна:

б н = 1

для всех

n

, если

b = 1

Степени $-1$ чередуются между $1$ и $-1$ , поскольку $n$ чередуется между четным и нечетным, и, таким образом, не стремятся к какому-либо пределу по мере $роста n$ .

Если $b < -1$ , $b н$ чередуется между все большими и большими положительными и отрицательными числами по мере того, как $n$ чередуется между четными и нечетными, и, таким образом, не стремится к какому-либо пределу по мере $роста n$ .

Если возведенное в степень число изменяется, стремясь к $1,$ поскольку показатель степени стремится к бесконечности, то предел не обязательно является одним из указанных выше. Особо важным случаем является

(1 + 1/ п) н \to е

при

n \to \infty

См. § Экспоненциальную функцию ниже.

Другие ограничения, в частности ограничения на выражения, принимающие неопределенную форму , описаны в § Пределы полномочий ниже.

Силовые функции [ править ]

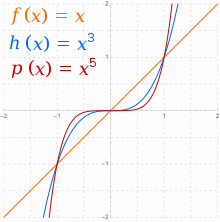
Действительные функции формы $f(x)=cx^{n}$ , где $c\neq 0$ , иногда называют степенными функциями. ^[25] Когда $n$ является целым числом и $n\geq 1$ существуют два основных семейства: для $n$ даже и для $n$ странный. В целом для $c>0$ , когда $n$ даже $f(x)=cx^{n}$ будет стремиться к положительной бесконечности с увеличением $x$ , а также в сторону положительной бесконечности с уменьшением $x$ . Все графики семейства четных степенных функций имеют общий вид $y=cx^{2}$ , сглаживая больше в середине, так как $n$ увеличивается. ^[26] Функции с такой симметрией ( $f(-x)=f(x)$ ) называются четными функциями .

Когда $n$ странно, $f(x)$ асимптотическое поведение меняется с положительного $x$ к отрицательному $x$ . Для $c>0$ , $f(x)=cx^{n}$ также будет стремиться к положительной бесконечности с увеличением $x$ , но в сторону отрицательной бесконечности с уменьшением $x$ . Все графики семейства нечетных степенных функций имеют общий вид $y=cx^{3}$ , сглаживая больше в середине, так как $n$ увеличивается и теряет всякую плоскостность там, на прямой, для $n=1$ . Функции с такой симметрией ( $f(-x)=-f(x)$ ) называются нечетными функциями .

Для $c<0$ , в каждом случае верно противоположное асимптотическое поведение. ^[26]

Таблица степеней десятичных цифр [ править ]

н	н ²	н ³	н ⁴	н ⁵	н ⁶	н ⁷	н ⁸	н ⁹	н ¹⁰
1	1	1	1	1	1	1	1	1	1
2	4	8	16	32	64	128	256	512	1024
3	9	27	81	243	729	2187	6561	19 683	59 049
4	16	64	256	1024	4096	16 384	65 536	262 144	1 048 576
5	25	125	625	3125	15 625	78 125	390 625	1 953 125	9 765 625
6	36	216	1296	7776	46 656	279 936	1 679 616	10 077 696	60 466 176
7	49	343	2401	16 807	117 649	823 543	5 764 801	40 353 607	282 475 249
8	64	512	4096	32 768	262 144	2 097 152	16 777 216	134 217 728	1 073 741 824
9	81	729	6561	59 049	531 441	4 782 969	43 046 721	387 420 489	3 486 784 401
10	100	1000	10 000	100 000	1 000 000	10 000 000	100 000 000	1 000 000 000	10 000 000 000

Рациональные показатели [ править ]

Если $x$ — неотрицательное действительное число , а $n$ — целое положительное число, $x^{1/n}$ или ${\sqrt[{n}]{x}}$ обозначает уникальный положительный действительный $n-й$ корень степени из $x$ , то есть уникальное положительное действительное число $y$ такое, что $y^{n}=x.$

Если $x$ — положительное действительное число и ${\frac {p}{q}}$ — рациональное число с $целыми числами p$ и $q > 0$ , тогда ${\textstyle x^{p/q}}$ определяется как

x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.

Равенство справа можно получить, полагая $y=x^{\frac {1}{q}},$ и писать $(x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.$

Если $r$ — положительное рациональное число, $0 р = 0$ по определению.

Все эти определения необходимы для расширения идентичности. $(x^{r})^{s}=x^{rs}$ рациональным показателям.

С другой стороны, существуют проблемы с распространением этих определений на базы, которые не являются положительными действительными числами. Например, отрицательное действительное число имеет действительный $корень n-й$ степени, который является отрицательным, если $,$ и n нечетное не имеет действительного корня, если $n$ четное. В последнем случае какой бы комплексный $корень n-$ й степени ни был выбран для $x^{\frac {1}{n}},$ личность $(x^{a})^{b}=x^{ab}$ не может быть удовлетворен. Например,

\left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.

См. § Действительные показатели степени и § Нецелые степени комплексных чисел для получения подробной информации о том, как можно решить эти проблемы.

Реальные показатели [ править ]

Для положительных действительных чисел возведение в степень до вещественных степеней можно определить двумя эквивалентными способами: либо путем расширения рациональных степеней до действительных чисел по непрерывности ( § Пределы рациональных показателей степени , ниже), либо с помощью логарифма основания и экспоненциальной функции. ( § Степени через логарифмы ниже). Результатом всегда является положительное действительное число, а тождества и свойства , показанные выше для целочисленных показателей, остаются верными и с этими определениями для действительных показателей. Второе определение используется чаще, поскольку оно напрямую обобщается на комплексные показатели.

С другой стороны, возведение в степень отрицательного действительного числа в степень гораздо сложнее определить последовательно, поскольку оно может быть недействительным и иметь несколько значений (см. § Действительные показатели степени с отрицательными основаниями ). Можно выбрать одно из этих значений, называемое главным значением , но нет выбора главного значения, для которого тождество

\left(b^{r}\right)^{s}=b^{rs}

правда; см. § Неисправность степенных и логарифмических тождеств . Поэтому возведение в степень с базисом, не являющимся положительным действительным числом, обычно рассматривается как многозначная функция .

Пределы рациональных показателей [ править ]

Поскольку любое иррациональное число может быть выражено как предел последовательности рациональных чисел, возведение в степень положительного действительного числа $b$ с произвольным действительным показателем $x$ может быть определено непрерывностью по правилу ^[27]

b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),

где предел берется только по рациональным значениям $r$ . Этот предел существует для каждого положительного $b$ и любого действительного $x$ .

Например, если $x = π$ , неограниченное десятичное представление $π = 3,14159...$ и монотонность рациональных степеней можно использовать для получения интервалов, ограниченных рациональными степенями, которые настолько малы, насколько это необходимо и должны содержать $b^{\pi }:$

\left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots

Итак, верхние границы и нижние границы интервалов образуют две последовательности , имеющие один и тот же предел, обозначаемые $b^{\pi }.$

Это определяет $b^{x}$ для каждого положительного $b$ и вещественного $x$ как непрерывной функции от $b$ и $x$ . См. также Четко определенное выражение . ^[28]

Экспоненциальная функция [ править ]

Показательную функцию часто определяют как $x\mapsto e^{x},$ где $e\approx 2.718$ это число Эйлера . Во избежание замкнутого круга рассуждений это определение здесь использовать нельзя. Итак, определение показательной функции, обозначаемой $\exp(x),$ и числа Эйлера, которые основаны только на возведении в степень с положительными целыми показателями. Затем набрасывается доказательство того, что если использовать определение возведения в степень, данное в предыдущих разделах, то

\exp(x)=e^{x}.

Существует много эквивалентных способов определения показательной функции , один из них —

\exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.

Надо $\exp(0)=1,$ и экспоненциальное тождество $\exp(x+y)=\exp(x)\exp(y)$ также имеет место, поскольку

\exp(x)\exp(y)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}\left(1+{\frac {y}{n}}\right)^{n}=\lim _{n\rightarrow \infty }\left(1+{\frac {x+y}{n}}+{\frac {xy}{n^{2}}}\right)^{n},

и член второго порядка ${\frac {xy}{n^{2}}}$ не влияет на предел, что дает $\exp(x)\exp(y)=\exp(x+y)$ .

Число Эйлера можно определить как $e=\exp(1)$ . Из предыдущих уравнений следует, что $\exp(x)=e^{x}$ когда $x$ является целым числом (это следует из определения возведения в степень с помощью многократного умножения). Если $х$ действительно, $\exp(x)=e^{x}$ является результатом определений, данных в предыдущих разделах, с использованием показательного тождества, если $x$ рационально, и непрерывности показательной функции в противном случае.

Предел, определяющий показательную функцию, сходится для каждого комплексного значения $x$ , и поэтому его можно использовать для расширения определения экспоненциальной функции. $\exp(z)$ , и поэтому $e^{z},$ от действительных чисел до любого комплексного аргумента $z$ . Эта расширенная экспоненциальная функция по-прежнему удовлетворяет экспоненциальному тождеству и обычно используется для определения возведения в степень для комплексного основания и показателя степени.

Степени через логарифмы [ править ]

Определение $е Икс$ поскольку показательная функция позволяет определить $b Икс$ для каждого положительного действительного числа $b$ в терминах экспоненты и логарифма . В частности, тот факт, что натуральный логарифм $ln(x)$ является обратным показательной функции $e Икс$ означает, что у человека есть

b=\exp(\ln b)=e^{\ln b}

для каждого $b > 0$ . За сохранение идентичности $(e^{x})^{y}=e^{xy},$ нужно иметь

b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}

Так, $e^{x\ln b}$ может использоваться как альтернативное определение $b Икс$ для любого положительного действительного $b$ . Это согласуется с определением, данным выше, с использованием рациональных показателей и непрерывности, с преимуществом прямого распространения на любой комплексный показатель.

показатели с положительной базой Комплексные действительной

Если $b$ — положительное действительное число, возведение в степень с основанием $b$ и комплексным показателем $z$ определяется с помощью экспоненциальной функции с комплексным аргументом (см. конец § Экспоненциальная функция выше) как

b^{z}=e^{(z\ln b)},

где $\ln b$ обозначает натуральный логарифм числа $b$ .

Это удовлетворяет тождеству

b^{z+t}=b^{z}b^{t},

В общем, ${\textstyle \left(b^{z}\right)^{t}}$ не определено, поскольку $b С$ это не действительное число. Если придается значение возведению комплексного числа в степень (см. § Нецелые степени комплексных чисел ниже), то, как правило, имеем

\left(b^{z}\right)^{t}\neq b^{zt},

если только $z$ не является вещественным или $t не$ является целым числом.

Формула Эйлера ,

e^{iy}=\cos y+i\sin y,

позволяет выразить форму полярную $b^{z}$ в терминах действительной и мнимой частей z $,$ а именно

b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),

где абсолютное значение тригонометрического коэффициента равно единице. Это является результатом

b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).

Нецелые степени комплексных чисел [ править ]

В предыдущих разделах возведение в степень с нецелыми показателями было определено только для положительных действительных оснований. Для других базисов трудности возникают уже в, казалось бы, простом случае $корней n-$ й степени, т. е. показателей степени $1/n,$ где $n$ — положительное целое число. Хотя общая теория возведения в степень с нецелыми показателями применима к $корням n-$ й степени, этот случай заслуживает рассмотрения в первую очередь, поскольку в нем нет необходимости использовать комплексные логарифмы , и поэтому его легче понять.

$n-$ ные корни комплексного числа [ править ]

Каждое ненулевое комплексное число $z$ можно записать в полярной форме как

z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),

где $\rho$ является абсолютным значением z $,$ и $\theta$ это его аргумент . Аргумент определяется до целого числа, кратного $2 π$ ; это означает, что если $\theta$ является аргументом комплексного числа, то $\theta +2k\pi$ также является аргументом одного и того же комплексного числа для каждого целого числа $k$ .

Полярная форма произведения двух комплексных чисел получается путем умножения абсолютных значений и сложения аргументов. Отсюда следует, что полярную форму $корня n$ -й степени комплексного числа можно получить, взяв $корень n$ -й степени из абсолютного значения и разделив его аргумент на $n$ :

\left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.

Если $2\pi$ добавляется в $\theta$ , комплексное число не меняется, но при этом добавляется $2i\pi /n$ к аргументу корня $n-$ й степени и предоставляет новый $корень n-$ й степени. Это можно сделать $n$ раз и получить $корни n$ $-й$ степени комплексного числа.

Обычно $выбирают один из корней n$ $-й$ в качестве главного корня степени . Обычно выбирают $корень n-й$ степени, для которого $-\pi <\theta \leq \pi ,$ то есть $корень n-$ й степени, имеющий наибольшую действительную часть, а если их два, то корень с положительной мнимой частью. Это делает главный $n-й$ корень степени непрерывной функцией во всей комплексной плоскости, за исключением отрицательных действительных значений подкоренного выражения . Эта функция равна обычному $корню n-$ й степени для положительных действительных подкоренных чисел. Для отрицательных вещественных подкоренных чисел и нечетных показателей главный $корень n-$ й степени недействителен, хотя обычный $корень n-$ й степени действителен. Аналитическое продолжение показывает, что главный $корень n-$ й степени представляет собой уникальную комплексную дифференцируемую функцию, продолжающую обычный $корень n-$ й степени на комплексную плоскость без неположительных действительных чисел.

Если комплексное число перемещается вокруг нуля путем увеличения его аргумента, после приращения $2\pi ,$ комплексное число возвращается в исходное положение, а его $n-$ корни й степени переставляются по кругу (они умножаются на $e^{2i\pi /n}$ ). Это показывает, что невозможно определить $корневую функцию n-$ й степени, непрерывную во всей комплексной плоскости.

Корни единства [ править ]

Корни $n-$ й степени из единицы — это $n$ комплексных чисел таких, что $w н = 1$ , где $n$ — положительное целое число. Они возникают в различных областях математики, например, в дискретном преобразовании Фурье или алгебраических решениях алгебраических уравнений ( резольвента Лагранжа ).

Корни $n$ $-й$ степени из единицы — это $n$ первых степеней числа. $\omega =e^{\frac {2\pi i}{n}}$ , то есть $1=\omega ^{0}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1}.$ Корни $n-$ й степени из единицы, обладающие этим порождающим свойством, называются примитивными $n-$ корнями й степени из единицы ; они имеют форму $\omega ^{k}=e^{\frac {2k\pi i}{n}},$ с $k$ взаимно простым с $n$ . Уникальный примитивный квадратный корень из единицы равен $-1;$ примитивные четвертые корни из единицы - это $i$ и $-i.$

Корни $n-$ й степени из единицы позволяют выразить все $корни n-$ й степени комплексного числа $z$ как $произведения n$ заданных $n-й$ корней $степени из z$ на $корень n-$ й степени из единицы.

Геометрически $корни n-$ й степени из единицы лежат на единичной окружности комплексной плоскости в вершинах правильного n $-$ угольника с одной вершиной, принадлежащей вещественному числу 1.

Как число $e^{\frac {2k\pi i}{n}}$ является примитивным $корнем n-й$ степени из единицы с наименьшим положительным аргументом , его называют главным примитивным $корнем n-$ й степени из единицы , иногда сокращают до главного $корня n-$ й степени из единицы , хотя эту терминологию можно спутать с главным значением $1^{1/n}$ , что равно 1. ^[29]^[30]^[31]

Комплексное возведение в степень [ править ]

Определение возведения в степень с помощью сложных базисов приводит к трудностям, аналогичным описанным в предыдущем разделе, за исключением того, что, как правило, существует бесконечно много возможных значений для $z^{w}$ . Таким образом, либо главное значение определяется $значений z , либо$ , которое не является непрерывным для вещественных и неположительных $z^{w}$ определяется как многозначная функция .

Во всех случаях комплексный логарифм используется для определения комплексного возведения в степень как

z^{w}=e^{w\log z},

где $\log z$ - это используемый вариант комплексного логарифма, то есть функция или многозначная функция , такая что

e^{\log z}=z

для каждого $z$ в своей области определения .

Основная ценность [ править ]

Главное значение комплексного логарифма — это уникальная непрерывная функция, обычно обозначаемая $\log ,$ такой, что для любого ненулевого комплексного числа $z$ ,

e^{\log z}=z,

и аргумент z $$ удовлетворяет

-\pi <\operatorname {Arg} z\leq \pi .

Главное значение комплексного логарифма не определено для $z=0,$ он разрывен при отрицательных действительных значениях $z$ и голоморфен ( т. е. комплексно дифференцируем) в других местах. Если $z$ действительное и положительное значение, главным значением комплексного логарифма является натуральный логарифм: $\log z=\ln z.$

Основная ценность $z^{w}$ определяется как $z^{w}=e^{w\log z},$ где $\log z$ – главное значение логарифма.

Функция $(z,w)\to z^{w}$ голоморфна, за исключением окрестности точек, где $z$ вещественна и неположительна.

Если $z$ действительное и положительное, главное значение $z^{w}$ равно своему обычному значению, определенному выше. Если $w=1/n,$ где $n$ — целое число, это главное значение такое же, как определенное выше.

Многозначная функция [ править ]

В некоторых контекстах существует проблема разрыва основных ценностей $\log z$ и $z^{w}$ при отрицательных действительных значениях $z$ . В этом случае полезно рассматривать эти функции как многозначные функции .

Если $\log z$ обозначает одно из значений многозначного логарифма (обычно его главное значение), остальные значения $2ik\pi +\log z,$ где $k$ — любое целое число. Аналогично, если $z^{w}$ является одним значением возведения в степень, тогда остальные значения определяются выражением

e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},

где $k$ — любое целое число.

Различные значения $k$ дают разные значения $z^{w}$ если только $w$ не является рациональным числом , то есть существует целое число $d$ такое, что $dw$ является целым числом. Это является следствием периодичности показательной функции, точнее, того, что $e^{a}=e^{b}$ если и только если $a-b$ является целым числом, кратным $2\pi i.$

Если $w={\frac {m}{n}}$ - рациональное число с $m$ и $n$ взаимно простыми целыми числами с $n>0,$ затем $z^{w}$ имеет ровно $n$ значений. В случае $m=1,$ эти значения такие же, как те, которые описаны в § $n-$ тых корнях комплексного числа . Если $w$ — целое число, существует только одно значение, согласующееся со значением § Целочисленных показателей .

Многозначное возведение в степень голоморфно для $z\neq 0,$ в том смысле, что его график состоит из нескольких листов, каждый из которых определяет голоморфную функцию в окрестности каждой точки. Если $z$ меняется непрерывно по окружности вокруг $0$ , то после поворота значение $z^{w}$ изменился лист.

Вычисление [ править ]

Каноническая форма $x+iy$ из $z^{w}$ может быть вычислено из канонической формы $z$ и $w$ . Хотя это можно описать одной формулой, удобнее разделить вычисления на несколько этапов.

Полярная z $.$ форма Если $z=a+ib$ является канонической формой $z$ ( $a$ и $b$ действительны), то его полярная форма равна $z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),$ где $\rho ={\sqrt {a^{2}+b^{2}}}$ и $\theta =\operatorname {atan2} (a,b)$ (см. atan2 для определения этой функции).
Логарифм z $$ . Главное значение этого логарифма равно $\log z=\ln \rho +i\theta ,$ где $\ln$ обозначает натуральный логарифм . Остальные значения логарифма получаются сложением $2ik\pi$ для любого целого числа $k$ .
Каноническая форма $w\log z.$ Если $w=c+di$ где $c$ и $d$ действительны, значения $w\log z$ являются $w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),$ главное значение, соответствующее $k=0.$
Конечный результат . Использование личностей $e^{x+y}=e^{x}e^{y}$ и $e^{y\ln x}=x^{y},$ каждый получает $z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),$ с $k=0$ за основную стоимость.

Примеры [ править ]

$i^{i}$
Полярная форма $i$ равна $i=e^{i\pi /2},$ и ценности $\log i$ таким образом $\log i=i\left({\frac {\pi }{2}}+2k\pi \right).$ Следует, что $i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.$ Итак, все значения $i^{i}$ реальны, главным из которых является $e^{-{\frac {\pi }{2}}}\approx 0.2079.$
$(-2)^{3+4i}$
Аналогично, полярная форма $-2$ равна $-2=2e^{i\pi }.$ Итак, описанный выше метод дает значения ${\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}$ В этом случае все значения имеют один и тот же аргумент. $4\ln 2,$ и разные абсолютные значения.

В обоих примерах все значения $z^{w}$ есть тот же аргумент. В более общем смысле это верно тогда и только тогда, когда часть w $действительная$ является целым числом.

Ошибка тождества степени и логарифма [ править ]

Некоторые тождества для степеней и логарифмов для положительных действительных чисел не будут работать для комплексных чисел, независимо от того, насколько комплексные степени и комплексные логарифмы определяются как однозначные функции . Например:

Журнал идентификации $(b Икс) = x \cdot log b$ выполняется всякий раз, когда $b$ — положительное действительное число, а $x$ — действительное число. Но для главной ветви комплексного логарифма имеем
$\log((-i)^{2})=\log(-1)=i\pi \neq 2\log(-i)=2\log(e^{-i\pi /2})=2\,{\frac {-i\pi }{2}}=-i\pi$
Независимо от того, какая ветвь логарифма используется, аналогичный сбой тождества будет существовать. Лучшее, что можно сказать (если использовать только этот результат), это то, что:
$\log w^{z}\equiv z\log w{\pmod {2\pi i}}$
Это тождество не выполняется даже при рассмотрении log как многозначной функции. Возможные значения $log(w С)$ содержат те из $z \cdot log w$ как собственное подмножество . Используя $Log(w)$ для основного значения $log(w)$ и $m$ , $n$ в качестве любых целых чисел, возможные значения обеих сторон таковы:
${\begin{aligned}\left\{\log w^{z}\right\}&=\left\{z\cdot \operatorname {Log} w+z\cdot 2\pi in+2\pi im\mid m,n\in \mathbb {Z} \right\}\\\left\{z\log w\right\}&=\left\{z\operatorname {Log} w+z\cdot 2\pi in\mid n\in \mathbb {Z} \right\}\end{aligned}}$
Личности $(до н.э.) Икс = б Икс с Икс$ и $(б / к) Икс = б Икс / с Икс$ действительны, когда $b$ и $c$ — положительные действительные числа, а $x$ — действительное число. Но для основных ценностей есть $(-1\cdot -1)^{\frac {1}{2}}=1\neq (-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1$ и $\left({\frac {1}{-1}}\right)^{\frac {1}{2}}=(-1)^{\frac {1}{2}}=i\neq {\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i$ С другой стороны, когда $x$ является целым числом, тождества действительны для всех ненулевых комплексных чисел. Если возведение в степень рассматривать как многозначную функцию, то возможные значения $(-1 \cdot -1) 1/2$ являются ${1, -1}$ . Тождество справедливо, но если сказать, что ${1} = {(-1 \cdot -1) 1/2}$ это неверно.
Личность ( e ^Икс) ^и = и ^ху справедливо для действительных чисел x и y , но предположение его истинности для комплексных чисел приводит к следующему парадоксу , открытому в 1827 году Клаузеном : ^[32] Для любого целого числа n мы имеем:
1. $e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e$
2. $\left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad$ (принимая $(1+2\pi in)$ -я мощность обеих сторон)
3. $e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad$ (с использованием $\left(e^{x}\right)^{y}=e^{xy}$ и расширяя показатель степени)
4. $e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad$ (с использованием $e^{x+y}=e^{x}e^{y}$ )
5. $e^{-4\pi ^{2}n^{2}}=1\qquad$ (деление на $е$ )
но это неверно, когда целое число n не равно нулю. Ошибка заключается в следующем: по определению, $e^{y}$ $е^{y}$ это обозначение для $\exp(y),$ $\exp(y),$ истинная функция и $x^{y}$ $x^{y}$ это обозначение для $\exp(y\log x),$ $\exp (y\log x),$ что является многозначной функцией. Таким образом, обозначение неоднозначно, когда x = e . Здесь, прежде чем расширять показатель степени, вторая строка должна быть
$\exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).$
$\exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).$
Поэтому при расширении показателя степени неявно предполагалось, что $\log \exp z=z$ $\log \exp z=z$ для комплексных значений z , что неверно, поскольку комплексный логарифм многозначен. Другими словами, неправильное тождество ( e ^Икс) ^и = и ^ху должно быть заменено идентификатором
$\left(e^{x}\right)^{y}=e^{y\log e^{x}},$
$\left(e^{x}\right)^{y} = e^{y\log e^{x}},$
что является истинным тождеством между многозначными функциями.

и трансцендентность Иррациональность

Если $b$ — положительное действительное алгебраическое число , а $x$ — рациональное число, то $b Икс$ является алгебраическим числом. Это следует из теории алгебраических расширений . Это остается верным, если $b$ — любое алгебраическое число, и в этом случае все значения $b Икс$ (как многозначная функция ) являются алгебраическими. Если $x$ иррационально значения (то есть не рационально ), и $b$ и $x$ алгебраические, теорема Гельфонда – Шнайдера утверждает, что все $b Икс$ являются трансцендентными (то есть не алгебраическими), за исключением случая, когда $b$ равно $0$ или $1$ .

Другими словами, если $x$ иррационально и $b\not \in \{0,1\},$ тогда хотя бы один из $b$ , $x$ и $b Икс$ является трансцендентальным.

Целые степени в алгебре [ править ]

Определение возведения в степень с положительными целыми показателями как повторяющегося умножения может применяться к любой ассоциативной операции, обозначаемой как умножение. ^{[номер 2]} Определение $х 0$ требует, кроме того, существования мультипликативного тождества . ^[33]

Алгебраическая структура , состоящая из множества вместе с ассоциативной операцией, обозначаемой мультипликативно, и мультипликативным тождеством, обозначаемым $1$ , является моноидом . В таком моноиде возведение в степень элемента $x$ определяется индуктивно формулой

$x^{0}=1,$
$x^{n+1}=xx^{n}$ для каждого неотрицательного целого числа $n$ .

Если $n$ — отрицательное целое число, $x^{n}$ определяется только в том случае, если $x$ имеет мультипликативную обратную величину . ^[34] В этом случае инверсия $x$ обозначается $x -1$ , и $х н$ определяется как $\left(x^{-1}\right)^{-n}.$

Возведение в степень с целыми показателями подчиняется следующим законам для $x$ и $y$ в алгебраической структуре и $целых чисел m$ и $n$ :

{\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{if }}xy=yx,{\text{and, in particular, if the multiplication is commutative.}}\end{aligned}}

Эти определения широко используются во многих областях математики, особенно для групп , колец , полей , квадратных матриц (образующих кольцо). Они применимы также к функциям из множества самому себе, которые образуют моноид при композиции функций . Сюда входят, в частности, геометрические преобразования и эндоморфизмы любой математической структуры .

Когда есть несколько операций, которые могут повторяться, обычно повторяющуюся операцию указывают, помещая ее символ в верхнем индексе перед показателем степени. Например, если $f$ — действительная функция , значение которой можно умножать, $f^{n}$ обозначает возведение в степень относительно умножения, а $f^{\circ n}$ может обозначать возведение в степень относительно композиции функций . То есть,

(f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),

и

(f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).

Обычно, $(f^{n})(x)$ обозначается $f(x)^{n},$ пока $(f^{\circ n})(x)$ обозначается $f^{n}(x).$

В группе [ править ]

Мультипликативная группа — это набор с ассоциативной операцией , обозначаемой как умножение, который имеет единичный элемент и такой, что каждый элемент имеет обратный.

Итак, если $G$ — группа, $x^{n}$ определяется для каждого $x\in G$ и каждое целое число $n$ .

Совокупность всех степеней элемента группы образует подгруппу . Группа (или подгруппа), состоящая из всех степеней определенного элемента $x,$ является циклической группой, порожденной $x$ . Если все степени $x$ различны, группа изоморфна аддитивной группе. $\mathbb {Z}$ целых чисел. противном случае циклическая группа конечна (она имеет конечное число элементов), а число ее элементов равно порядку x $В$ . Если порядок $x$ равен $n$ , то $x^{n}=x^{0}=1,$ а циклическая группа, порожденная $x$ , состоит из $n$ первых степеней $x$ (начиная безразлично с показателя $0$ или $1$ ).

Порядок элементов играет фундаментальную роль в теории групп . Например, порядок элемента в конечной группе всегда является делителем числа элементов группы (порядка группы ). Возможные порядки элементов группы важны при изучении строения группы (см. теоремы Силова ), а также при классификации конечных простых групп .

Надстрочные обозначения также используются для спряжения ; то есть $г час = час -1 gh$ , где $g$ и $h$ — элементы группы. Это обозначение нельзя путать с возведением в степень, поскольку верхний индекс не является целым числом. Мотивация этого обозначения состоит в том, что сопряжение подчиняется некоторым законам возведения в степень, а именно $(g^{h})^{k}=g^{hk}$ и $(gh)^{k}=g^{k}h^{k}.$

На ринге [ править ]

В кольце может случиться так, что некоторые ненулевые элементы удовлетворяют условиям $x^{n}=0$ для некоторого целого числа $n$ . Такой элемент называется нильпотентным . В коммутативном кольце нильпотентные элементы образуют идеал , называемый нильрадикалом кольца.

Если нильрадикал привести к нулевому идеалу (т. е. если $x\neq 0$ подразумевает $x^{n}\neq 0$ для любого натурального числа $n$ ) коммутативное кольцо называется приведенным . Приведенные кольца важны в алгебраической геометрии , поскольку координатное кольцо аффинного алгебраического множества всегда является приведенным кольцом.

задан идеал $I$ в коммутативном кольце $R$ , набор элементов $R$ , имеющих степень в $I,$ идеалом, называемым радикалом I. $является$ В более общем смысле, если Нильрадикал – это радикал нулевого идеала . Радикальный идеал — это идеал, равный своему собственному радикалу. В полиномиальном кольце $k[x_{1},\ldots ,x_{n}]$ над полем $k$ идеал радикален тогда и только тогда, когда он представляет собой набор всех полиномов, равных нулю на аффинном алгебраическом множестве (это следствие Nullstellensatz Гильберта ).

Матрицы и линейные операторы [ править ]

Если $A$ — квадратная матрица, то произведение $A$ на саму себя $n$ раз называется степенью матрицы . Также $A^{0}$ определяется как единичная матрица, ^[35] и если $A$ обратимо, то $A^{-n}=\left(A^{-1}\right)^{n}$ .

Степени матрицы часто появляются в контексте дискретных динамических систем , где матрица $A$ выражает переход от вектора состояния $x$ некоторой системы к следующему состоянию $Ax$ системы. ^[36] стандартная интерпретация цепи Маркова Это , например, . Затем $A^{2}x$ — состояние системы после двух временных шагов и т. д.: $A^{n}x$ — состояние системы после $n$ шагов по времени. Сила матрицы $A^{n}$ — матрица перехода между состоянием сейчас и состоянием в момент времени $n$ шагов в будущем. Таким образом, вычисление степеней матрицы эквивалентно решению эволюции динамической системы. Во многих случаях степени матрицы целесообразно вычислять с помощью собственных значений и собственных векторов .

Помимо матриц, более общие линейные операторы можно возводить в степень и . Примером является производный оператор исчисления, $d/dx$ , который является линейным оператором, действующим на функции $f(x)$ дать новую функцию $(d/dx)f(x)=f'(x)$ . я степень $n-$ оператора дифференцирования представляет собой $n-$ ю производную:

\left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).

Эти примеры относятся к дискретным показателям линейных операторов, но во многих случаях желательно также определять степени таких операторов с непрерывными показателями. Это отправная точка математической теории полугрупп . ^[37]Точно так же, как вычисление степеней матрицы с дискретными показателями позволяет решать дискретные динамические системы, так же вычисление степеней матрицы с непрерывными показателями решает системы с непрерывной динамикой. Примеры включают подходы к решению уравнения теплопроводности , уравнения Шредингера , волнового уравнения и других уравнений в частных производных, включая эволюцию во времени. Частный случай возведения оператора производной в степень в нецелую степень называется дробной производной , которая вместе с дробным интегралом является одной из основных операций дробного исчисления .

Конечные поля [ править ]

Поле тому — это алгебраическая структура, в которой определены умножение, сложение, вычитание и деление и удовлетворяют свойствам ассоциативности умножения и , что каждый ненулевой элемент имеет мультипликативный обратный . Это означает, что возведение в степень с целыми показателями четко определено, за исключением неположительных степеней $0$ . Типичными примерами являются поля комплексных чисел , действительные числа и рациональные числа , рассмотренные ранее в этой статье, которые бесконечны .

Конечное поле — это поле с конечным числом элементов. Это количество элементов является либо простым числом , либо степенью простого числа ; то есть имеет вид $q=p^{k},$ где $p$ — простое число, а $k$ — целое положительное число. Для каждого такого $q$ существуют поля с $q$ элементами. Все поля с $q$ элементами изоморфны , что позволяет, в общем, работать так, как если бы существовало только одно поле с $q$ элементами, обозначаемое $\mathbb {F} _{q}.$

Надо

x^{q}=x

для каждого $x\in \mathbb {F} _{q}.$

элемент Примитивный в $\mathbb {F} _{q}$ — это элемент $g$ такой, что набор $q - 1$ первых степеней $g$ (т. е. $\{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}$ ) равно множеству ненулевых элементов $\mathbb {F} _{q}.$ Есть $\varphi (p-1)$ примитивные элементы в $\mathbb {F} _{q},$ где $\varphi$ — это полная функция Эйлера .

В $\mathbb {F} _{q},$ первокурсника мечты личность

(x+y)^{p}=x^{p}+y^{p}

верно для показателя $p$ . Как $x^{p}=x$ в $\mathbb {F} _{q},$ Отсюда следует, что карта

{\begin{aligned}F\colon {}&\mathbb {F} _{q}\to \mathbb {F} _{q}\\&x\mapsto x^{p}\end{aligned}}

линейна по $\mathbb {F} _{q},$ и является полевым автоморфизмом , называемым автоморфизмом Фробениуса . Если $q=p^{k},$ поле $\mathbb {F} _{q}$ имеет $k$ автоморфизмов, которые являются $k$ первыми степенями (при композиции ) $F$ . Другими словами, группа Галуа $\mathbb {F} _{q}$ является циклическим порядка $k$ , порожденным автоморфизмом Фробениуса.

Обмен ключами Диффи -Хеллмана — это применение возведения в степень в конечных полях, которое широко используется для безопасной связи . Он использует тот факт, что возведение в степень требует недорогих вычислений, тогда как обратная операция, дискретный логарифм , требует больших вычислительных затрат. Точнее, если $g$ является примитивным элементом в $\mathbb {F} _{q},$ затем $g^{e}$ может быть эффективно вычислено с возведением в степень путем возведения в квадрат для любого $e$ , даже если $q$ велико, хотя не существует известного практического вычислительного алгоритма, который позволял бы извлекать $e$ из $g^{e}$ если $q$ достаточно велико.

Степени множеств [ править ]

Декартово произведение двух наборов $S$ и $T$ — это набор упорядоченных пар. $(x,y)$ такой, что $x\in S$ и $y\in T.$ Эта операция не является ни коммутативной , ни ассоциативной , но обладает этими свойствами с точностью до канонических изоморфизмов , которые позволяют идентифицировать, например, $(x,(y,z)),$ $((x,y),z),$ и $(x,y,z).$

Это позволяет определить $n-$ ю степень $S^{n}$ множества $S$ как множества всех $n$ - кортежей $(x_{1},\ldots ,x_{n})$ элементов $S$ .

Когда $S$ наделен некоторой структурой, часто бывает, что $S^{n}$ естественно наделен аналогичной структурой. В этом случае термин « прямое произведение » обычно используется вместо «декартово произведение», а возведение в степень обозначает структуру произведения. Например $\mathbb {R} ^{n}$ (где $\mathbb {R}$ обозначает действительные числа) обозначает декартово произведение $n$ копий $\mathbb {R} ,$ а также их прямое произведение в виде векторных пространств , топологических пространств , колец и т. д.

Устанавливается как показатель степени [ править ]

n $$ -кортеж $(x_{1},\ldots ,x_{n})$ элементов $S$ можно рассматривать как функцию от $\{1,\ldots ,n\}.$ Это обобщается до следующих обозначений.

Учитывая два набора $S$ и $T$ , набор всех функций от $T$ до $S$ обозначается $S^{T}$ . Это экспоненциальное обозначение оправдано следующими каноническими изоморфизмами (первый из них см. Карринг ):

(S^{T})^{U}\cong S^{T\times U},

S^{T\sqcup U}\cong S^{T}\times S^{U},

где $\times$ обозначает декартово произведение, а $\sqcup$ непересекающийся союз .

Можно использовать множества в качестве показателей для других операций над множествами, обычно для прямых сумм абелевых групп , векторных пространств или модулей . Чтобы отличить прямые суммы от прямых произведений, показатель прямой суммы ставится в круглые скобки. Например, $\mathbb {R} ^{\mathbb {N} }$ обозначает векторное пространство бесконечных последовательностей действительных чисел, а $\mathbb {R} ^{(\mathbb {N} )}$ векторное пространство тех последовательностей, которые имеют конечное число ненулевых элементов. Последний имеет базис , состоящий из последовательностей ровно с одним ненулевым элементом, равным $1$ , тогда как базисы Гамеля первого не могут быть явно описаны (поскольку их существование предполагает лемму Цорна ).

В этом контексте $2$ может представлять набор $\{0,1\}.$ Так, $2^{S}$ обозначает набор степеней S $,$ то есть набор функций от $S$ до $\{0,1\},$ можно отождествить с набором подмножеств S путем $который$ сопоставления каждой функции прообразом 1 $с$ .

Это согласуется с возведением в степень кардинальных чисел в том смысле, что $| С Т | = | С | | Т |$ , где $| Х |$ является мощностью $X$ .

В теории категорий [ править ]

В категории множеств морфизмы собой между множествами $X$ и $Y$ функции из $X$ в $Y.$ представляют В результате множество функций от $X$ до $Y$ , которое обозначается $Y^{X}$ в предыдущем разделе также можно обозначить $\hom(X,Y).$ Изоморфизм $(S^{T})^{U}\cong S^{T\times U}$ можно переписать

\hom(U,S^{T})\cong \hom(T\times U,S).

Это означает, что функтор «возведение в степень $Т$ » является правосопряженным к функтору «прямое произведение на $Т$ ».

Это обобщается до определения возведения в степень в категории , в которой существуют конечные прямые произведения : в такой категории функтор $X\to X^{T}$ является, если он существует, правосопряженным функтором $Y\to T\times Y.$ Категория называется декартовой замкнутой категорией , если существуют прямые произведения и функтор $Y\to X\times Y$ имеет правый сопряженный для каждого $T$ .

Повторное возведение в степень [ править ]

Так же, как возведение в степень натуральных чисел обусловлено повторным умножением, можно определить операцию, основанную на повторном возведении в степень; эту операцию иногда называют гипер-4 или тетрацией . Итерация тетрации приводит к другой операции и так далее, концепции, называемой гипероперацией . Эта последовательность операций выражается функцией Аккермана и обозначением стрелки вверх Кнута . Точно так же, как возведение в степень растет быстрее, чем умножение, которое растет быстрее, чем сложение, так и тетрация растет быстрее, чем возведение в степень. При оценке $(3, 3)$ функции сложения, умножения, возведения в степень и тетрации дают 6, 9, 27 и 7 625 597 484 987 ( $=3 27 = 3 33 = 33$ ) соответственно.

Пределы полномочий [ править ]

Ноль в нулевой степени дает ряд примеров пределов неопределенного вида 0 ⁰. Пределы в этих примерах существуют, но имеют разные значения, что показывает, что функция двух переменных $x и$ не имеет предела в точке $(0,0)$ . Можно рассмотреть, в каких точках эта функция имеет предел.

Точнее, рассмотрим функцию $f(x,y)=x^{y}$ определено на $D=\{(x,y)\in \mathbf {R} ^{2}:x>0\}$ . Тогда $D$ можно рассматривать как подмножество $R 2$ (то есть набор всех пар $(x, y)$ с $x$ , $y$ , принадлежащими расширенной прямой действительных чисел $R = [-\infty, +\infty]$ , наделенной топологией произведения ), которая будет содержать точки, в которых функция $f$ имеет предел.

Фактически, $f$ имеет предел во всех точках накопления D $,$ , кроме $(0, 0)$ , $(+\infty, 0)$ ( $1, +\infty)$ и $(1, -\infty)$ . ^[38] Соответственно, это позволяет определить степени $x и$ по непрерывности всякий раз, когда $0 \leq x \leq +\infty$ , $-\infty \leq y \leq +\infty$ , за исключением $00$ , $(+\infty) 0$ , $1 +\infty$ и $1 -\infty$ , которые остаются неопределенными формами.

При этом определении по непрерывности получаем:

$Икс +\infty = +\infty$ и $x -\infty знак равно 0$ , когда $1 < x \leq +\infty$ .
$Икс +\infty = 0$ и $х -\infty = +\infty$ , когда $0 \leq x < 1$ .
$0 и = 0$ и $(+\infty) и = +\infty$ , когда $0 < y \leq +\infty$ .
$0 и = +\infty$ и $(+\infty) и знак равно 0$ , когда $-\infty \leq y < 0$ .

Эти степени получаются путем установления пределов $x и$ для положительных значений $x$ . Этот метод не позволяет определить $x и$ когда $x < 0$ , поскольку пары $(x, y)$ с $x < 0$ не являются точками накопления $D$ .

С другой стороны, когда $n$ — целое число, степень $x н$ уже имеет смысл для всех значений $x$ , включая отрицательные. Это может сделать определение $0 н = +\infty$ , полученное выше для отрицательного $n,$ проблематично, когда $n$ нечетно, поскольку в этом случае $x н \to +\infty,$ поскольку $x$ стремится к $0$ через положительные значения, но не через отрицательные.

Эффективные вычисления с целочисленными показателями [ править ]

Вычисление $б н$ использование повторного умножения требует $n - 1$ операций умножения, но его можно вычислить более эффективно, как показано в следующем примере. Чтобы вычислить $2100$ , примените правило Горнера к показателю степени 100, записанному в двоичном формате:

100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2))

.

Затем вычислите следующие члены по порядку, читая правило Горнера справа налево.

2 ² = 4
2 (2 ²) = 2 ³ = 8
(2 ³) ² = 2 ⁶ = 64
(2 ⁶) ² = 2 ¹² = 4096
(2 ¹²) ² = 2 ²⁴ = 16 777 216
2 (2 ²⁴) = 2 ²⁵ = 33 554 432
(2 ²⁵) ² = 2 ⁵⁰ = 1 125 899 906 842 624
(2 ⁵⁰) ² = 2 ¹⁰⁰ = 1 267 650 600 228 229 401 496 703 205 376

Для этой серии шагов требуется всего 8 умножений вместо 99.

В общем, количество операций умножения, необходимых для вычисления $b н$ можно свести к $\sharp n+\lfloor \log _{2}n\rfloor -1,$ с помощью возведения в степень возведением в квадрат , где $\sharp n$ количество $единиц$ в двоичном представлении n $.$ обозначает Для некоторых показателей степени (100 в их число не входит) количество умножений можно дополнительно уменьшить путем вычисления и использования минимального возведения в степень цепочки сложения . Нахождение минимальной последовательности умножений (цепочки сложения показателя минимальной длины) для $b н$ — сложная задача, для которой в настоящее время не известны эффективные алгоритмы (см. Задача о сумме подмножества ), но доступно множество достаточно эффективных эвристических алгоритмов. ^[39] Однако в практических вычислениях возведение в степень возведением в степень достаточно эффективно, и его гораздо проще реализовать.

Итерированные функции [ править ]

Композиция функций — это бинарная операция , определенная для функций таким образом, что кодомен функции, написанной справа, включается в домен функции, написанной слева. Он обозначается $g\circ f,$ и определяется как

(g\circ f)(x)=g(f(x))

для каждого $x$ в области $f$ .

Если область определения функции $f$ равна ее кодомену, можно составлять функцию сама с собой произвольное количество раз, и это определяет $n$ -ю степень компонуемой функции, обычно называемую $n-$ й итерацией функции. Таким образом $f^{n}$ обычно обозначает $n-ю$ итерацию $f$ ; например, $f^{3}(x)$ означает $f(f(f(x))).$ ^[40]

Когда умножение определено в кодомене функции, это определяет умножение на функции, поточечное умножение , которое вызывает другое возведение в степень. При использовании функциональной записи два вида возведения в степень обычно различаются путем размещения показателя функциональной итерации перед круглыми скобками, заключающими в себе аргументы функции, и помещения показателя поточечного умножения после круглых скобок. Таким образом $f^{2}(x)=f(f(x)),$ и $f(x)^{2}=f(x)\cdot f(x).$ Когда функциональная нотация не используется, устранение неоднозначности часто достигается путем помещения символа композиции перед показателем степени; например $f^{\circ 3}=f\circ f\circ f,$ и $f^{3}=f\cdot f\cdot f.$ По историческим причинам показатель степени повторного умножения ставится перед аргументом некоторых конкретных функций, обычно тригонометрических функций . Так, $\sin ^{2}x$ и $\sin ^{2}(x)$ оба означают $\sin(x)\cdot \sin(x)$ и не $\sin(\sin(x)),$ что, во всяком случае, редко учитывается. Исторически сложилось так, что разные авторы использовали несколько вариантов этих обозначений. ^[41]^[42]^[43]

В этом контексте показатель $-1$ обозначает всегда обратную функцию , если она существует. Так $\sin ^{-1}x=\sin ^{-1}(x)=\arcsin x.$ Для мультипликативных обратных дробей обычно используются, как в $1/\sin(x)={\frac {1}{\sin x}}.$

В языках программирования [ править ]

Языки программирования обычно выражают возведение в степень либо как инфиксный оператор , либо как приложение функции, поскольку они не поддерживают верхние индексы. Наиболее распространенным символом оператора возведения в степень является каретка ( ^). Исходная версия ASCII включала символ стрелки вверх ( ↑), предназначенный для возведения в степень, но в 1967 году он был заменен на каретку , поэтому каретка стала обычным явлением в языках программирования. ^[44] Обозначения включают в себя:

x ^ y: AWK , BASIC , J , MATLAB , Wolfram Language ( Mathematica ), R , Microsoft Excel , Analytica , TeX (и его производные), TI-BASIC , bc (для целочисленных показателей), Haskell (для неотрицательных целочисленных показателей), Lua , и большинство систем компьютерной алгебры .
x ** y. Набор символов Фортрана не включал строчные буквы или знаки препинания, кроме +-*/()&=.,' и так использовал ** для возведения в степень ^[45]^[46] (первоначальная версия использовалась a xx b вместо. ^[47]). Многие другие языки последовали этому примеру: Ada , Z Shell , KornShell , Bash , COBOL , CoffeeScript , Fortran , FoxPro , Gnuplot , Groovy , JavaScript , OCaml , F# , Perl , PHP , PL/I , Python , Rexx , Ruby , SAS , Seed7. , Tcl , ABAP , Mercury , Haskell (для показателей с плавающей запятой), Turing и VHDL .
x ↑ y: Алгол Справочный язык , Commodore BASIC , TRS-80 Level II/III BASIC . ^[48]^[49]
x ^^ y: Haskell (для дробной базы, целых показателей), D .
x⋆y: АПЛ .

В большинстве языков программирования с инфиксным оператором возведения в степень он правоассоциативен , то есть a^b^c интерпретируется как a^(b^c). ^[50] Это потому что (a^b)^c равно a^(b*c)и, следовательно, не так полезен. В некоторых языках он левоассоциативен, особенно в Algol , Matlab и языке формул Microsoft Excel .

Другие языки программирования используют функциональную нотацию:

(expt x y): Общий Лисп .
pown x y: F# (для целочисленной базы и целочисленной экспоненты).

Третьи обеспечивают возведение в степень только как часть стандартных библиотек :

pow(x, y): C , C++ (в math библиотека).
Math.Pow(x, y): С# .
math:pow(X, Y): Эрланг .
Math.pow(x, y): Джава .
[Math]::Pow(x, y): PowerShell .

В некоторых статически типизированных языках, которые отдают приоритет безопасности типов , таких как Rust , возведение в степень выполняется с помощью множества методов:

x.pow(y) для x и y как целые числа
x.powf(y) для x и y как числа с плавающей запятой
x.powi(y) для x как поплавок и y как целое число

См. также [ править ]

v т Это	Арифметические выражения	Полиномиальные выражения	Алгебраические выражения	Выражения закрытой формы	Аналитические выражения	Математические выражения
Постоянный	Да	Да	Да	Да	Да	Да
Элементарная арифметическая операция	Да	Только сложение, вычитание и умножение.	Да	Да	Да	Да
я конечен	Да	Да	Да	Да	Да	Да
Конечный продукт	Да	Да	Да	Да	Да	Да
Конечная цепная дробь	Да	Нет	Да	Да	Да	Да
Переменная	Нет	Да	Да	Да	Да	Да
Они полностью объяснят	Нет	Да	Да	Да	Да	Да
Целочисленный корень n-й степени	Нет	Нет	Да	Да	Да	Да
Рациональный показатель	Нет	Нет	Да	Да	Да	Да
Целочисленный факториал	Нет	Нет	Да	Да	Да	Да
Иррациональный показатель	Нет	Нет	Нет	Да	Да	Да
Экспоненциальная функция	Нет	Нет	Нет	Да	Да	Да
Логарифм	Нет	Нет	Нет	Да	Да	Да
Тригонометрическая функция	Нет	Нет	Нет	Да	Да	Да
Обратная тригонометрическая функция	Нет	Нет	Нет	Да	Да	Да
Гиперболическая функция	Нет	Нет	Нет	Да	Да	Да
Обратная гиперболическая функция	Нет	Нет	Нет	Да	Да	Да
Корень многочлена , не являющегося алгебраическим решением	Нет	Нет	Нет	Нет	Да	Да
Гамма-функция и факториал нецелого числа	Нет	Нет	Нет	Нет	Да	Да
Функция Бесселя	Нет	Нет	Нет	Нет	Да	Да
Специальная функция	Нет	Нет	Нет	Нет	Да	Да
Бесконечная сумма (ряд) (включая степенной ряд )	Нет	Нет	Нет	Нет	Только конвергентный	Да
Бесконечный продукт	Нет	Нет	Нет	Нет	Только конвергентный	Да
Бесконечная цепная дробь	Нет	Нет	Нет	Нет	Только конвергентный	Да
Лимит	Нет	Нет	Нет	Нет	Нет	Да
Производная	Нет	Нет	Нет	Нет	Нет	Да
интеграл	Нет	Нет	Нет	Нет	Нет	Да

Примечания [ править ]

^ Существует три распространенных обозначения умножения : $x\times y$ чаще всего используется для явных чисел и на очень элементарном уровне; $xy$ наиболее распространен при переменных ; использовании $x\cdot y$ используется, чтобы подчеркнуть, что речь идет об умножении, или когда пропуск знака умножения может сбить с толку.
^ В более общем смысле, степенной ассоциативности . для определения достаточно

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с ^д ^Это Никамп, Дуэйн. «Основные правила возведения в степень» . Математическое понимание . Проверено 27 августа 2020 г.
^ Вайсштейн, Эрик В. «Власть» . Математический мир . Проверено 27 августа 2020 г.
^ «Экспонента | Этимология экспоненты по этимонлине» .
^ Перейти обратно: ^а ^б Ротман, Джозеф Дж. (2015). Продвинутая современная алгебра, часть 1 . Аспирантура по математике . Том. 165 (3-е изд.). Провиденс, Род-Айленд: Американское математическое общество . п. 130, сн. 4. ISBN 978-1-4704-1554-9 .
^ Сабо, Арпад (1978). Начало греческой математики . Синтез Историческая библиотека. Том. 17. Перевод А. М. Унгара. Дордрехт: Д. Рейдель . п. 37 . ISBN 90-277-0819-3 .
^ Перейти обратно: ^а ^б О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Этимология некоторых распространенных математических терминов» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
^ Болл, У. В. Роуз (1915). Краткий обзор истории математики (6-е изд.). Лондон: Макмиллан . п. 38 .
^ Архимед. (2009). ПЕСОЧНИК. В Т. Хите (ред.), «Работы Архимеда: отредактированные в современных обозначениях с вводными главами» (Собрание Кембриджской библиотеки – Математика, стр. 229–232). Кембридж: Издательство Кембриджского университета. дои : 10.1017/CBO9780511695124.017 .
^ Перейти обратно: ^а ^б Куинион, Майкл . «Зензизензизензик» . Всемирные слова . Проверено 16 апреля 2020 г.
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Абул Хасан ибн Али аль-Калсади» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
^ Каджори, Флориан (1928). История математических обозначений . Том. 1. Компания «Открытый суд». п. 102.
^ Каджори, Флориан (1928). История математических обозначений . Том. 1. Лондон: Издательство Open Court . п. 344 .
^ «Самые ранние известные варианты использования некоторых математических слов (E)» . 23.06.2017.
^ Штифель, Майкл (1544). Полная арифметика . Нюрнберг: Йоханнес Петрейус . п. 235 в.
^ Каджори, Флориан (1928). История математических обозначений . Том. 1. Компания «Открытый суд». п. 204.
^ Декарт, Рене (1637). « Геометрия ». Рассуждение о методе [...] . Лейден: Ян Мэр. п. 299. И аа , или $а 2$ , чтобы умножить $a$ на себя; И $имеет 3$ , чтобы еще раз умножить его на $a$ и, таким образом, до бесконечности (И $aa$ или $a 2$ , чтобы умножить $a$ на себя; и $ 3$ , чтобы еще раз умножить его на $a$ и, таким образом, до бесконечности).
^ Самое последнее использование в этом смысле, на которое ссылается OED, относится к 1806 году ( «инволюция» . Оксфордский словарь английского языка (онлайн-изд.). Издательство Оксфордского университета . подписка или членство в участвующей организации ( Требуется .) ).
^ Эйлер, Леонард (1748). Введение в анализ бесконечно малых (на латыни). Том. I. Лозанна: Марк-Мишель Буске. стр. 69, 98–99. Поэтому в первую очередь следует рассматривать показательные величины, или степени, показатель степени которых сам по себе является переменной величиной. Ибо ясно, что такого рода величины нельзя отнести к алгебраическим функциям, так как в этих показателях имеют место только константы.
^ Ходж, Джонатан К.; Шликер, Стивен; Сандсторм, Тед (2014). Абстрактная алгебра: исследовательский подход . ЦРК Пресс. п. 94. ИСБН 978-1-4665-6706-1 .
^ Ахац, Томас (2005). Технический цех Математика (3-е изд.). Промышленная пресса. п. 101. ИСБН 978-0-8311-3086-2 .
^ Кноблох, Эберхард (1994). «Бесконечное в математике Лейбница - историографический метод понимания в контексте». У Костаса Гавроглу; Жан Кристианидис; Эфтимиос Николаидис (ред.). Тенденции в историографии науки . Бостонские исследования в области философии науки. Спрингер Нидерланды. п. 276. дои : 10.1007/978-94-017-3596-4_20 . ISBN 9789401735964 . Положительная степень нуля бесконечно мала, отрицательная степень нуля бесконечна.
^ Бронштейн Илья Николаевич ; Семендяев, Константин Адольфович (1987) [1945]. «2.4.1.1. Определение арифметических выражений» Написано в Лейпциге, Германия. В Гроше, Гюнтер; Зиглер, Виктор; Зиглер, Доротея (ред.). по математике ( Карманный справочник на немецком языке). Том 1. Перевод Циглера Виктора. Вайс, Юрген (23-е изд.). Тун, Швейцария / Франкфурт-на-Майне, Германия: Verlag Harri Deutsch (и BG Teubner Verlagsgesellschaft , Лейпциг). стр. 115–120, 802. ISBN. 3-87144-492-8 .
^ Олвер, Фрэнк У.Дж.; Лозье, Дэниел В.; Буасверт, Рональд Ф.; Кларк, Чарльз В., ред. (2010). Справочник NIST по математическим функциям . Национальный институт стандартов и технологий (NIST), Министерство торговли США , Издательство Кембриджского университета . ISBN 978-0-521-19225-5 . МР 2723248 . [1]
^ Зейдлер, Эберхард [на немецком языке] ; Шварц, Ганс Рудольф; Хакбуш, Вольфганг ; Людерер, Бернд [на немецком языке] ; Блат, Йохен; Шид, Александр; Демпе, Стефан; Ванка, Герт ; Хромкович, Юрай ; Готвальд, Зигфрид (2013) [2012]. Зейдлер, Эберхард [на немецком языке] (ред.). Справочник Springer по математике I (на немецком языке). Том I (1-е изд.). Берлин/Гейдельберг, Германия: Springer Spektrum , Springer Fachmedien Wiesbaden . п. 590. ИСБН 978-3-658-00284-8 . (xii+635 страниц)
^ Хасс, Джоэл Р.; Хайль, Кристофер Э.; Вейр, Морис Д.; Томас, Джордж Б. (2018). Исчисление Томаса (14 изд.). Пирсон. стр. 7–8. ISBN 9780134439020 .
^ Перейти обратно: ^а ^б Антон, Ховард; Бивенс, Ирландия; Дэвис, Стивен (2012). Исчисление: ранние трансценденталисты (9-е изд.). Джон Уайли и сыновья. п. 28 . ISBN 9780470647691 .
^ Денлингер, Чарльз Г. (2011). Элементы реального анализа . Джонс и Бартлетт. стр. 278–283. ISBN 978-0-7637-7947-4 .
^ Тао, Теренс (2016). «Пределы последовательностей» . Анализ И. Тексты и чтения по математике. Том. 37. С. 126–154. дои : 10.1007/978-981-10-1789-6_6 . ISBN 978-981-10-1789-6 .
^ Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Стоун, Клиффорд (2001). Введение в алгоритмы (второе изд.). МТИ Пресс . ISBN 978-0-262-03293-3 . Интернет-ресурс. Архивировано 30 сентября 2007 г. на Wayback Machine .
^ Калл, Пол; Флахайв, Мэри ; Робсон, Робби (2005). Разностные уравнения: от кроликов к хаосу ( Тексты для студентов по математике под ред.). Спрингер. ISBN 978-0-387-23234-8 . Определено на стр. 351.
^ Вайсштейн, Эрик В. «Главный корень единства» . Математический мир .
^ Штайнер, Дж.; Клаузен, Т.; Абель, Нильс Хенрик (1827). «Проблемы и предложения: первые нужно решить, потом доказать». Журнал чистой и прикладной математики . 2 :286-287.
^ Бурбаки, Николя (1970). Алгебра . Спрингер. И.2.
^ Блум, Дэвид М. (1979). Линейная алгебра и геометрия . Издательство Кембриджского университета. п. 45 . ISBN 978-0-521-29324-2 .
^ Глава 1, Элементарная линейная алгебра, 8E, Говард Антон.
^ Стрэнг, Гилберт (1988). Линейная алгебра и ее приложения (3-е изд.). Брукс-Коул. Глава 5.
^ Э. Хилле, Р.С. Филлипс: Функциональный анализ и полугруппы . Американское математическое общество, 1975.
^ Николя Бурбаки, Общая топология , V.4.2.
^ Гордон, DM (1998). «Обзор методов быстрого возведения в степень» (PDF) . Журнал алгоритмов . 27 : 129–146. CiteSeerX 10.1.1.17.7076 . дои : 10.1006/jagm.1997.0913 . Архивировано из оригинала (PDF) 23 июля 2018 г. Проверено 11 января 2024 г.
^ Пеано, Джузеппе (1903). Математическая форма (на французском языке). Полет. IV. п. 229.
^ Гершель, Джон Фредерик Уильям (1813) [1812-11-12]. «О замечательном применении теоремы Котса». Философские труды Лондонского королевского общества . 103 (Часть 1). Лондон: Лондонское королевское общество , напечатано W. Bulmer and Co., Cleveland-Row, St. James's, продано G. and W. Nicol, Pall-Mall: 8–26 [10]. дои : 10.1098/rstl.1813.0005 . JSTOR 107384 . S2CID 118124706 .
^ Гершель, Джон Фредерик Уильям (1820). «Часть III. Раздел I. Примеры прямого метода разностей» . Сборник примеров приложений исчисления конечных разностей . Кембридж, Великобритания: Отпечатано Дж. Смитом, продано компанией J. Deighton & Sons. С. 1–13 [5–6]. Архивировано из оригинала 04 августа 2020 г. Проверено 4 августа 2020 г. [2] (Примечание. Здесь Гершель ссылается на свою работу 1813 года и упоминает Ганса Генриха Бюрмана .) более старую работу
^ Каджори, Флориан (1952) [март 1929]. История математических обозначений . Том. 2 (3-е изд.). Чикаго, США: Издательская компания «Открытый суд» . стр. 100-1 108, 176–179, 336, 346 978-1-60206-714-1 . Проверено 18 января 2016 г.
^ Ричард Гиллам (2003). Демистификация Unicode: Практическое руководство программиста по стандарту кодирования . п. 33. ISBN 0201700522 .
^ Бэкус, Джон Уорнер ; Бибер, Р.Дж.; Бест, Шелдон Ф.; Гольдберг, Ричард ; Херрик, Харлан Л.; Хьюз, РА; Митчелл, LB; Нельсон, Роберт А.; Натт, Рой ; Сэйр, Дэвид ; Шеридан, Питер Б.; Стерн, Гарольд; Зиллер, Ирвинг (15 октября 1956 г.). Сэйр, Дэвид (ред.). Система автоматического кодирования FORTRAN для IBM 704 EDPM: Справочное руководство программиста (PDF) . Нью-Йорк, США: Отдел прикладных наук и отдел исследований в области программирования, International Business Machines Corporation . п. 15. Архивировано (PDF) из оригинала 4 июля 2022 г. Проверено 4 июля 2022 г. (2+51+1 стр.)
^ Брайс Карнахан; Джеймс О. Уилкс (1968). Введение в цифровые вычисления и FORTRAN IV с приложениями MTS . стр. 2–2, 2–6.
^ Бэкус, Джон Уорнер ; Херрик, Харлан Л.; Нельсон, Роберт А.; Зиллер, Ирвинг (10 ноября 1954 г.). Бэкус, Джон Уорнер (ред.). Спецификации для: Система перевода математических формул IBM, FORTRAN (PDF) (предварительный отчет). Нью-Йорк, США: Группа исследования программирования, Отдел прикладных наук, Международная корпорация Business Machines . стр. 4, 6. Архивировано (PDF) из оригинала 29 марта 2022 г. Проверено 4 июля 2022 г. (29 страниц)
^ Данелюк, Тимоти «Тим» А. (9 августа 1982 г.). «BASCOM — БЕЙСИК-компилятор для TRS-80 I и II» . Инфомир . Обзоры программного обеспечения. Том. 4, нет. 31. Popular Computing, Inc., стр. 41–42. Архивировано из оригинала 07 февраля 2020 г. Проверено 6 февраля 2020 г.
^ «80 Содержание» . 80 Микро (45). 1001001, Inc .: 5 октября 1983 г. ISSN 0744-7868 . Проверено 6 февраля 2020 г.
^ Роберт В. Себеста (2010). Понятия языков программирования . стр. 100-1 130, 324. ISBN 0136073476 .

[3] Существует три распространенных обозначения умножения : $x\times y$ чаще всего используется для явных чисел и на очень элементарном уровне; $xy$ наиболее распространен при переменных ; использовании $x\cdot y$ используется, чтобы подчеркнуть, что речь идет об умножении, или когда пропуск знака умножения может сбить с толку.

[34] В более общем смысле, степенной ассоциативности . для определения достаточно

[:1-1] Перейти обратно: ^а ^б ^с ^д ^Это Никамп, Дуэйн. «Основные правила возведения в степень» . Математическое понимание . Проверено 27 августа 2020 г.

[2] Вайсштейн, Эрик В. «Власть» . Математический мир . Проверено 27 августа 2020 г.

[4] «Экспонента | Этимология экспоненты по этимонлине» .

[Rotman-5] Перейти обратно: ^а ^б Ротман, Джозеф Дж. (2015). Продвинутая современная алгебра, часть 1 . Аспирантура по математике . Том. 165 (3-е изд.). Провиденс, Род-Айленд: Американское математическое общество . п. 130, сн. 4. ISBN 978-1-4704-1554-9 .

[6] Сабо, Арпад (1978). Начало греческой математики . Синтез Историческая библиотека. Том. 17. Перевод А. М. Унгара. Дордрехт: Д. Рейдель . п. 37 . ISBN 90-277-0819-3 .

[MacTutor-7] Перейти обратно: ^а ^б О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Этимология некоторых распространенных математических терминов» . MacTutor Архив истории математики . Университет Сент-Эндрюс .

[8] Болл, У. В. Роуз (1915). Краткий обзор истории математики (6-е изд.). Лондон: Макмиллан . п. 38 .

[9] Архимед. (2009). ПЕСОЧНИК. В Т. Хите (ред.), «Работы Архимеда: отредактированные в современных обозначениях с вводными главами» (Собрание Кембриджской библиотеки – Математика, стр. 229–232). Кембридж: Издательство Кембриджского университета. дои : 10.1017/CBO9780511695124.017 .

[worldwidewords-10] Перейти обратно: ^а ^б Куинион, Майкл . «Зензизензизензик» . Всемирные слова . Проверено 16 апреля 2020 г.

[11] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Абул Хасан ибн Али аль-Калсади» . MacTutor Архив истории математики . Университет Сент-Эндрюс .

[12] Каджори, Флориан (1928). История математических обозначений . Том. 1. Компания «Открытый суд». п. 102.

[cajori-13] Каджори, Флориан (1928). История математических обозначений . Том. 1. Лондон: Издательство Open Court . п. 344 .

[14] «Самые ранние известные варианты использования некоторых математических слов (E)» . 23.06.2017.

[15] Штифель, Майкл (1544). Полная арифметика . Нюрнберг: Йоханнес Петрейус . п. 235 в.

[16] Каджори, Флориан (1928). История математических обозначений . Том. 1. Компания «Открытый суд». п. 204.

[17] Декарт, Рене (1637). « Геометрия ». Рассуждение о методе [...] . Лейден: Ян Мэр. п. 299. И аа , или $а 2$ , чтобы умножить $a$ на себя; И $имеет 3$ , чтобы еще раз умножить его на $a$ и, таким образом, до бесконечности (И $aa$ или $a 2$ , чтобы умножить $a$ на себя; и $ 3$ , чтобы еще раз умножить его на $a$ и, таким образом, до бесконечности).

[18] Самое последнее использование в этом смысле, на которое ссылается OED, относится к 1806 году ( «инволюция» . Оксфордский словарь английского языка (онлайн-изд.). Издательство Оксфордского университета . подписка или членство в участвующей организации ( Требуется .) ).

[Euler_1748-19] Эйлер, Леонард (1748). Введение в анализ бесконечно малых (на латыни). Том. I. Лозанна: Марк-Мишель Буске. стр. 69, 98–99. Поэтому в первую очередь следует рассматривать показательные величины, или степени, показатель степени которых сам по себе является переменной величиной. Ибо ясно, что такого рода величины нельзя отнести к алгебраическим функциям, так как в этих показателях имеют место только константы.

[20] Ходж, Джонатан К.; Шликер, Стивен; Сандсторм, Тед (2014). Абстрактная алгебра: исследовательский подход . ЦРК Пресс. п. 94. ИСБН 978-1-4665-6706-1 .

[21] Ахац, Томас (2005). Технический цех Математика (3-е изд.). Промышленная пресса. п. 101. ИСБН 978-0-8311-3086-2 .

[22] Кноблох, Эберхард (1994). «Бесконечное в математике Лейбница - историографический метод понимания в контексте». У Костаса Гавроглу; Жан Кристианидис; Эфтимиос Николаидис (ред.). Тенденции в историографии науки . Бостонские исследования в области философии науки. Спрингер Нидерланды. п. 276. дои : 10.1007/978-94-017-3596-4_20 . ISBN 9789401735964 . Положительная степень нуля бесконечно мала, отрицательная степень нуля бесконечна.

[Bronstein_1987-23] Бронштейн Илья Николаевич ; Семендяев, Константин Адольфович (1987) [1945]. «2.4.1.1. Определение арифметических выражений» Написано в Лейпциге, Германия. В Гроше, Гюнтер; Зиглер, Виктор; Зиглер, Доротея (ред.). по математике ( Карманный справочник на немецком языке). Том 1. Перевод Циглера Виктора. Вайс, Юрген (23-е изд.). Тун, Швейцария / Франкфурт-на-Майне, Германия: Verlag Harri Deutsch (и BG Teubner Verlagsgesellschaft , Лейпциг). стр. 115–120, 802. ISBN. 3-87144-492-8 .

[NIST_2010-24] Олвер, Фрэнк У.Дж.; Лозье, Дэниел В.; Буасверт, Рональд Ф.; Кларк, Чарльз В., ред. (2010). Справочник NIST по математическим функциям . Национальный институт стандартов и технологий (NIST), Министерство торговли США , Издательство Кембриджского университета . ISBN 978-0-521-19225-5 . МР 2723248 . [1]

[Zeidler_2013-25] Зейдлер, Эберхард [на немецком языке] ; Шварц, Ганс Рудольф; Хакбуш, Вольфганг ; Людерер, Бернд [на немецком языке] ; Блат, Йохен; Шид, Александр; Демпе, Стефан; Ванка, Герт ; Хромкович, Юрай ; Готвальд, Зигфрид (2013) [2012]. Зейдлер, Эберхард [на немецком языке] (ред.). Справочник Springer по математике I (на немецком языке). Том I (1-е изд.). Берлин/Гейдельберг, Германия: Springer Spektrum , Springer Fachmedien Wiesbaden . п. 590. ИСБН 978-3-658-00284-8 . (xii+635 страниц)

[26] Хасс, Джоэл Р.; Хайль, Кристофер Э.; Вейр, Морис Д.; Томас, Джордж Б. (2018). Исчисление Томаса (14 изд.). Пирсон. стр. 7–8. ISBN 9780134439020 .

[Calculus:_Early_Transcendentals-27] Перейти обратно: ^а ^б Антон, Ховард; Бивенс, Ирландия; Дэвис, Стивен (2012). Исчисление: ранние трансценденталисты (9-е изд.). Джон Уайли и сыновья. п. 28 . ISBN 9780470647691 .

[Denlinger-28] Денлингер, Чарльз Г. (2011). Элементы реального анализа . Джонс и Бартлетт. стр. 278–283. ISBN 978-0-7637-7947-4 .

[29] Тао, Теренс (2016). «Пределы последовательностей» . Анализ И. Тексты и чтения по математике. Том. 37. С. 126–154. дои : 10.1007/978-981-10-1789-6_6 . ISBN 978-981-10-1789-6 .

[30] Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Стоун, Клиффорд (2001). Введение в алгоритмы (второе изд.). МТИ Пресс . ISBN 978-0-262-03293-3 . Интернет-ресурс. Архивировано 30 сентября 2007 г. на Wayback Machine .

[31] Калл, Пол; Флахайв, Мэри ; Робсон, Робби (2005). Разностные уравнения: от кроликов к хаосу ( Тексты для студентов по математике под ред.). Спрингер. ISBN 978-0-387-23234-8 . Определено на стр. 351.

[32] Вайсштейн, Эрик В. «Главный корень единства» . Математический мир .

[Clausen1827-33] Штайнер, Дж.; Клаузен, Т.; Абель, Нильс Хенрик (1827). «Проблемы и предложения: первые нужно решить, потом доказать». Журнал чистой и прикладной математики . 2 :286-287.

[35] Бурбаки, Николя (1970). Алгебра . Спрингер. И.2.

[36] Блум, Дэвид М. (1979). Линейная алгебра и геометрия . Издательство Кембриджского университета. п. 45 . ISBN 978-0-521-29324-2 .

[37] Глава 1, Элементарная линейная алгебра, 8E, Говард Антон.

[38] Стрэнг, Гилберт (1988). Линейная алгебра и ее приложения (3-е изд.). Брукс-Коул. Глава 5.

[39] Э. Хилле, Р.С. Филлипс: Функциональный анализ и полугруппы . Американское математическое общество, 1975.

[40] Николя Бурбаки, Общая топология , V.4.2.

[41] Гордон, DM (1998). «Обзор методов быстрого возведения в степень» (PDF) . Журнал алгоритмов . 27 : 129–146. CiteSeerX 10.1.1.17.7076 . дои : 10.1006/jagm.1997.0913 . Архивировано из оригинала (PDF) 23 июля 2018 г. Проверено 11 января 2024 г.

[Peano_1903-42] Пеано, Джузеппе (1903). Математическая форма (на французском языке). Полет. IV. п. 229.

[Herschel_1813-43] Гершель, Джон Фредерик Уильям (1813) [1812-11-12]. «О замечательном применении теоремы Котса». Философские труды Лондонского королевского общества . 103 (Часть 1). Лондон: Лондонское королевское общество , напечатано W. Bulmer and Co., Cleveland-Row, St. James's, продано G. and W. Nicol, Pall-Mall: 8–26 [10]. дои : 10.1098/rstl.1813.0005 . JSTOR 107384 . S2CID 118124706 .

[Herschel_1820-44] Гершель, Джон Фредерик Уильям (1820). «Часть III. Раздел I. Примеры прямого метода разностей» . Сборник примеров приложений исчисления конечных разностей . Кембридж, Великобритания: Отпечатано Дж. Смитом, продано компанией J. Deighton & Sons. С. 1–13 [5–6]. Архивировано из оригинала 04 августа 2020 г. Проверено 4 августа 2020 г. [2] (Примечание. Здесь Гершель ссылается на свою работу 1813 года и упоминает Ганса Генриха Бюрмана .) более старую работу

[Cajori_1929-45] Каджори, Флориан (1952) [март 1929]. История математических обозначений . Том. 2 (3-е изд.). Чикаго, США: Издательская компания «Открытый суд» . стр. 100-1 108, 176–179, 336, 346 978-1-60206-714-1 . Проверено 18 января 2016 г.

[46] Ричард Гиллам (2003). Демистификация Unicode: Практическое руководство программиста по стандарту кодирования . п. 33. ISBN 0201700522 .

[Sayre_1956-47] Бэкус, Джон Уорнер ; Бибер, Р.Дж.; Бест, Шелдон Ф.; Гольдберг, Ричард ; Херрик, Харлан Л.; Хьюз, РА; Митчелл, LB; Нельсон, Роберт А.; Натт, Рой ; Сэйр, Дэвид ; Шеридан, Питер Б.; Стерн, Гарольд; Зиллер, Ирвинг (15 октября 1956 г.). Сэйр, Дэвид (ред.). Система автоматического кодирования FORTRAN для IBM 704 EDPM: Справочное руководство программиста (PDF) . Нью-Йорк, США: Отдел прикладных наук и отдел исследований в области программирования, International Business Machines Corporation . п. 15. Архивировано (PDF) из оригинала 4 июля 2022 г. Проверено 4 июля 2022 г. (2+51+1 стр.)

[48] Брайс Карнахан; Джеймс О. Уилкс (1968). Введение в цифровые вычисления и FORTRAN IV с приложениями MTS . стр. 2–2, 2–6.

[Backus_1954-49] Бэкус, Джон Уорнер ; Херрик, Харлан Л.; Нельсон, Роберт А.; Зиллер, Ирвинг (10 ноября 1954 г.). Бэкус, Джон Уорнер (ред.). Спецификации для: Система перевода математических формул IBM, FORTRAN (PDF) (предварительный отчет). Нью-Йорк, США: Группа исследования программирования, Отдел прикладных наук, Международная корпорация Business Machines . стр. 4, 6. Архивировано (PDF) из оригинала 29 марта 2022 г. Проверено 4 июля 2022 г. (29 страниц)

[InfoWorld_1982-50] Данелюк, Тимоти «Тим» А. (9 августа 1982 г.). «BASCOM — БЕЙСИК-компилятор для TRS-80 I и II» . Инфомир . Обзоры программного обеспечения. Том. 4, нет. 31. Popular Computing, Inc., стр. 41–42. Архивировано из оригинала 07 февраля 2020 г. Проверено 6 февраля 2020 г.

[80Micro_1983-51] «80 Содержание» . 80 Микро (45). 1001001, Inc .: 5 октября 1983 г. ISSN 0744-7868 . Проверено 6 февраля 2020 г.

[52] Роберт В. Себеста (2010). Понятия языков программирования . стр. 100-1 130, 324. ISBN 0136073476 .

[1]

[2]

[номер 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[номер 2]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

v т Это Гипероперации
Primary	Successor (0) Addition (1) Multiplication (2) Exponentiation (3) Tetration (4) Pentation (5) Hexation (6)
Inverse for left argument	Predecessor (0) Subtraction (1) Division (2) Root extraction (3) Super-root (4)
Inverse for right argument	Predecessor (0) Subtraction (1) Division (2) Logarithm (3) Super-logarithm (4)
Related articles	Ackermann function Conway chained arrow notation Grzegorczyk hierarchy Knuth's up-arrow notation Steinhaus–Moser notation

v т Это Порядки величины времени
by powers of ten
Negative powers	<1 attosecond attosecond femtosecond picosecond nanosecond microsecond millisecond
Positive powers	second kilosecond megasecond gigasecond terasecond and longer