Центрированное квадратное число

В элементарной теории чисел центрированное квадратное число — это центрированное фигурное число , которое дает количество точек в квадрате с точкой в центре и всех других точек, окружающих центральную точку в последовательных квадратных слоях. То есть каждое центрированное квадратное число равно количеству точек на расстоянии заданного городского квартала от центральной точки на обычной квадратной решетке . Хотя центрированные квадратные числа, как и фигурные числа в целом, практически не имеют прямого практического применения, их иногда изучают в развлекательной математике из-за их элегантных геометрических и арифметических свойств.

Цифры для первых четырех центрированных квадратных чисел показаны ниже:


$C_{4,1}=1$			$C_{4,2}=5$			$C_{4,3}=13$			$C_{4,4}=25$

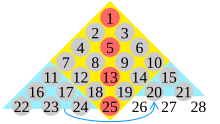
Каждое центрированное квадратное число представляет собой сумму последовательных квадратов. Пример: как показано на следующем рисунке треугольника Флойда , 25 — это число в центре квадрата, а также сумма квадрата 16 (желтый ромб, образованный в результате разрезания квадрата) и следующего меньшего квадрата 9 (сумма двух синих треугольников). ):

Отношения с другими фигурными числами [ править ]

Пусть Ck _{n , -} обычно представляют n е центрированное k -угольное число . ное n- центрированное квадратное число определяется по формуле:

C_{4,n}=n^{2}+(n-1)^{2}.

То есть n -е центрированное квадратное число представляет собой сумму n -го и ( n – 1)-го квадратных чисел . Следующий шаблон демонстрирует эту формулу:


$C_{4,1}=0+1$			$C_{4,2}=1+4$			$C_{4,3}=4+9$			$C_{4,4}=9+16$

Формулу также можно выразить как:

C_{4,n}={\frac {(2n-1)^{2}+1}{2}}.

То есть n -е квадратное число с центром равно половине n -го нечетного квадратного числа плюс 1, как показано ниже:


$C_{4,1}={\frac {1+1}{2}}$			$C_{4,2}={\frac {9+1}{2}}$			$C_{4,3}={\frac {25+1}{2}}$			$C_{4,4}={\frac {49+1}{2}}$

Как и все центрированные многоугольные числа , центрированные квадратные числа также могут быть выражены через треугольные числа :

C_{4,n}=1+4\ T_{n-1}=1+2{n(n-1)},

где

T_{n}={\frac {n(n+1)}{2}}={\binom {n+1}{2}}

— n- е треугольное число. Это можно легко увидеть, удалив центральную точку и разделив остальную часть фигуры на четыре треугольника, как показано ниже:


$C_{4,1}=1$			$C_{4,2}=1+4\times 1$			$C_{4,3}=1+4\times 3$			$C_{4,4}=1+4\times 6$

Разница между двумя последовательными октаэдрическими числами представляет собой центрированное квадратное число (Конвей и Гай, стр. 50).

Другой способ выражения центрированных квадратных чисел:

C_{4,n}=1+4\dim(SO(n)),

где

\dim(SO(n))={\frac {n(n-1)}{2}}.

Еще один способ выразить центрированные квадратные числа — через центрированные треугольные числа :

C_{4,n}={\frac {4C_{3,n}-1}{3}},

где

C_{3,n}=1+3{\frac {n(n-1)}{2}}.

Список центрированных квадратных чисел [ править ]

Первые центрированные квадратные числа ( C _{4, n} < 4500):

1 , 5 , 13 , 25 , 41 , 61 , 85 , 113 , 145 , 181 , 221 , 265, 313 , 365 , 421, 481, 545, 613, 685, 761, 841, 925, 1013, 05, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 41, 41, 4325, … (последовательность A001844 в ОЭИС ).

Свойства [ править ]

Все центрированные квадратные числа нечетны, и в базе 10 можно заметить, что цифра единицы соответствует шаблону 1-5-3-5-1.

Все центрированные квадратные числа и их делители имеют остаток 1 при делении на 4. Следовательно, все центрированные квадратные числа и их делители оканчиваются цифрой 1 или 5 по основанию 6 , 8 и 12 .

Каждое центрированное квадратное число, кроме 1, является гипотенузой ( пифагоровой тройки 3-4-5 , 5-12-13 , 7-24-25 , ...). Это в точности последовательность пифагорейских троек, в которой две самые длинные стороны отличаются на 1. (Пример: 5 ² + 12 ² = 13 ².)

Это не следует путать с отношением ( n – 1) ² + н ² = С _{4, п} . (Пример: 2 ² + 3 ² = 13 .)

Генерирующая функция [ править ]

Производящая функция, которая дает центрированные квадратные числа:

{\frac {(x+1)^{2}}{(1-x)^{3}}}=1+5x+13x^{2}+25x^{3}+41x^{4}+~...~.

Ссылки [ править ]

Альфред, У. (1962), « $n$ и $n + 1$ последовательные целые числа с равными суммами квадратов», Mathematics Magazine , 35 (3): 155–164, doi : 10.1080/0025570X.1962.11975326 , JSTOR 2688938 , MR 1571197 .
Апостол, Том М. (1976), Введение в аналитическую теорию чисел , Тексты для студентов по математике, Нью-Йорк-Гейдельберг: Springer-Verlag, ISBN 978-0-387-90163-3 , МР 0434929 , Збл 0335.10001 .
Бейлер, А.Х. (1964), «Отдых в теории чисел» , Нью-Йорк: Дувр, с. 125 .
Конвей, Джон Х .; Гай, Ричард К. (1996), Книга чисел , Нью-Йорк: Коперник, стр. 41–42 , ISBN. 0-387-97993-Х , МР 1411676 .