Практический номер

Демонстрация практичности числа 12

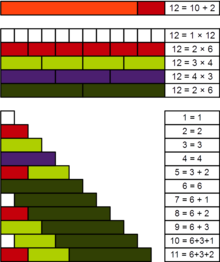
В теории чисел — практическое число или панарифмическое число. является положительным целым числом $n$ такие, что все меньшие положительные целые числа можно представить как суммы различных делителей числа. $n$. Например, 12 — практическое число, потому что все числа от 1 до 11 можно выразить как суммы его делителей 1, 2, 3, 4 и 6: как и сами эти делители, у нас есть 5 = ​​3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1 и 11 = 6 + 3 + 2.

Последовательность практических чисел (последовательность A005153 в OEIS ) начинается

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

Практические числа использовались Фибоначчи в его «Liber Abaci» (1202) в связи с проблемой представления рациональных чисел в виде египетских дробей . Фибоначчи формально не дает определения практических чисел, но он дает таблицу разложения египетских дробей для дробей с практическими знаменателями.

Название «практическое число» принадлежит Шринивасану (1948) . Он отметил, что «подразделения денег, весов и мер включают числа вроде 4, 12, 16, 20 и 28, которые обычно считаются настолько неудобными, что заслуживают замены степенями 10». Его частичная классификация этих чисел была завершена Стюартом (1954) и Серпинским (1955) . Эта характеристика позволяет определить, является ли число практичным, исследуя его простую факторизацию. Каждое четное совершенное число и каждая степень двойки также является практическим числом.

Также было показано, что практические числа аналогичны простым числам по многим своим свойствам.

Характеристика практических чисел

В исходной характеристике Шринивасана (1948) говорилось, что практическое число не может быть недостающим числом , то есть таким, у которого сумма всех делителей (включая 1 и само себя) меньше чем в два раза больше числа, если только недостача не равна единице. Если упорядоченный набор всех делителей практического числа $n$ является ${d_{1},d_{2},...,d_{j}}$ с $d_{1}=1$ и $d_{j}=n$, то утверждение Шринивасана можно выразить неравенством

$$2n\leq 1+\sum _{i=1}^{j}d_{i}.$$

Другими словами, упорядоченная последовательность всех делителей ${d_{1}<d_{2}<...<d_{j}}$ практического числа должна быть полной подпоследовательностью .

Эта частичная характеристика была расширена и дополнена Стюартом (1954) и Серпинским (1955), которые показали, что легко определить, является ли число практичным, исходя из его простой факторизации .Целое положительное число больше единицы с простой факторизацией $n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}$ (с простыми числами в отсортированном порядке $p_{1}<p_{2}<\dots <p_{k}$) практично тогда и только тогда, когда каждый из его простых факторов $p_{i}$ достаточно мал для $p_{i}-1$ иметь представление в виде суммы меньших делителей. Чтобы это было правдой, первое простое число $p_{1}$ должно равняться 2, и для каждого i от 2 до k каждое последующее простое число $p_{i}$ должно подчиняться неравенству

$p_{i}\leq 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\sigma (p_{1}^{\alpha _{1}})\sigma (p_{2}^{\alpha _{2}})\dots \sigma (p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},$

где $\sigma (x)$ обозначает делителей x . сумму Например, 2 × 3 ² × 29 × 823 = 429606 практично, поскольку приведенное выше неравенство справедливо для каждого из его простых множителей: 3 ≤ σ(2) + 1 = 4, 29 ≤ σ(2 × 3 ² ) + 1 = 40 и 823 ≤ σ(2 × 3 ² × 29) + 1 = 1171.

Условие, изложенное выше, является необходимым и достаточным для того, чтобы число было практичным. С одной стороны, это условие необходимо для того, чтобы иметь возможность представлять $p_{i}-1$ как сумма делителей $n$, потому что если бы неравенство не было верным, то даже сложение всех меньших делителей дало бы сумму, слишком малую для достижения $p_{i}-1$. В обратном направлении условие является достаточным, как показывает индукция. Более сильно, если факторизация $n$ удовлетворяет условию выше, то любое $m\leq \sigma (n)$ можно представить в виде суммы делителей $n$, выполнив следующую последовательность шагов:

• Индукцией по $j\in [1,\alpha _{k}]$, можно показать, что $p_{k}^{j}\leq 1+\sigma (n/p_{k}^{\alpha _{k}-(j-1)})$. Следовательно $p_{k}^{\alpha _{k}}\leq 1+\sigma (n/p_{k})$.
• Поскольку внутренности $[qp_{k}^{\alpha _{k}},qp_{k}^{\alpha _{k}}+\sigma (n/p_{k})]$ крышка $[1,\sigma (n)]$ для $1\leq q\leq \sigma (n/p_{k}^{\alpha _{k}})$, есть такой $q$ и некоторые $r\in [0,\sigma (n/p_{k})]$ такой, что $m=qp_{k}^{\alpha _{k}}+r$.
• С $q\leq \sigma (n/p_{k}^{\alpha _{k}})$ и $n/p_{k}^{\alpha _{k}}$ практическую эффективность можно показать по индукции, мы можем найти представление q в виде суммы делителей $n/p_{k}^{\alpha _{k}}$.
• С $r\leq \sigma (n/p_{k})$, и поскольку $n/p_{k}$ практическую эффективность можно показать по индукции, мы можем найти представление r в виде суммы делителей $n/p_{k}$.
• Делители, представляющие r вместе с $p_{k}^{\alpha _{k}}$ раз каждый из делителей, представляющих q , вместе образуют представление m как сумму делителей $n$.

Свойства

• Единственное нечетное практическое число — 1, потому что если $n$ нечетное число больше 2, то 2 не может быть выражено как сумма различных делителей числа. $n$. Более убедительно Шринивасан (1948) отмечает, что, кроме 1 и 2, каждое практическое число делится на 4 или 6 (или на то и другое).
• Произведение двух практических чисел также является практичным числом. Эквивалентно, множество всех практических чисел замкнуто при умножении. Более того, наименьшее общее кратное любых двух практических чисел также является практическим числом.
• Из приведенной выше характеристики Стюарта и Серпинского видно, что если $n$ это практическое число и $d$ является одним из его делителей, тогда $n\cdot d$ также должно быть практичным числом.
• В множестве всех практических чисел имеется примитивный набор практических чисел. Примитивное практическое число либо практично и не содержит квадратов , либо практично и при делении на любой из его простых множителей, показатель факторизации которого больше 1, больше не практично. Последовательность примитивных практических чисел (последовательность A267124 в OEIS ) начинается

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

• Каждое положительное целое число имеет практическое кратное. Например, для каждого целого числа $n$, его кратное $2^{\lfloor \log _{2}n\rfloor }n$ практичен.

Связь с другими классами чисел

Несколько других примечательных наборов целых чисел состоят только из практических чисел:

• Из приведенных выше свойств с $n$ практичное число и $d$ один из его делителей (т. $d|n$) затем $n\cdot d$ также должно быть практическим числом, поэтому шесть раз в каждой степени 3 должно быть практическим числом, так же как шесть раз в каждой степени 2.
• Каждая степень двойки является практическим числом. Степени двойки тривиально удовлетворяют характеристике практических чисел с точки зрения их разложения на простые множители: единственное простое число в их факторизации, p ₁ , равно двум, как и требуется.
• Каждое четное совершенное число также является практичным числом. Это следует из результата Леонарда Эйлера о том, что четное совершенное число должно иметь вид $2^{k-1}(2^{k}-1)$. Нечетная часть этой факторизации равна сумме делителей четной части, поэтому каждый нечетный простой делитель такого числа должен быть не более суммой делителей четной части числа. Следовательно, это число должно удовлетворять характеристике практических чисел. Аналогичный аргумент можно использовать, чтобы показать, что четное совершенное число, разделенное на 2, больше непрактично. Следовательно, каждое четное совершенное число также является примитивным практическим числом.
• Каждый первичный (продукт первого $i$ простые числа, для некоторых $i$) практично. Для первых двух первородных, второго и шестого, это ясно. Каждое последующее простое число образуется путем умножения простого числа. $p_{i}$ на меньшее простое число, которое делится как на два, так и на следующее меньшее простое число, $p_{i-1}$. По постулату Бертрана , $p_{i}<2p_{i-1}$, поэтому каждый последующий простой делитель в простом множителе меньше одного из делителей предыдущего простого числа. По индукции следует, что каждый первоначальный элемент удовлетворяет характеристике практических чисел. Поскольку первичное число по определению не содержит квадратов, оно также является примитивным практическим числом.
• Обобщая первоначальные числа, любое число, являющееся произведением ненулевых степеней первой $k$ простые числа также должны быть практичными. Сюда входят ( Рамануджана сложные числа числа, у которых делителей больше, чем у любого меньшего положительного целого числа), а также факториалы .

числа и

Если $n$ практично, то любое рациональное число вида $m/n$ с $m<n$ можно представить в виде суммы ${\textstyle \sum d_{i}/n}$ где каждый $d_{i}$ является явным делителем $n$. Каждый член этой суммы упрощается до единичной доли , поэтому такая сумма обеспечивает представление $m/n$ как египетская дробь . Например,

$${\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.$$

Фибоначчи в своей книге Liber Abaci 1202 года. перечисляет несколько методов поиска представлений рационального числа египетскими дробями. Из них первый — проверить, является ли само число уже единичной дробью, а второй — найти представление числителя в виде суммы делителей знаменателя, как описано выше. Этот метод гарантированно будет успешным только для практических знаменателей. Фибоначчи предоставляет таблицы этих представлений для дробей, имеющих в знаменателях практические числа 6, 8, 12, 20, 24, 60 и 100.

Восе (1985) показал, что каждое рациональное число $x/y$ имеет представление египетской дроби с $O({\sqrt {\log y}})$ условия. Доказательство предполагает нахождение последовательности практических чисел. $n_{i}$ со свойством, что каждое число меньше $n_{i}$ можно записать как сумму $O({\sqrt {\log n_{i-1}}})$ отдельные делители $n_{i}$. Затем, $i$ выбирается так, что $n_{i-1}<y<n_{i}$, и $xn_{i}$ делится на $y$ давая частное $q$ и остаток $r$. Из этих выборов следует, что ${\frac {x}{y}}={\frac {q}{n_{i}}}+{\frac {r}{yn_{i}}}$. Разложив оба числителя в правой части этой формулы в суммы делителей $n_{i}$ приводит к желаемому представлению египетской дроби. Тененбаум и Йокота (1990) используют аналогичную технику, включающую другую последовательность практических чисел, чтобы показать, что каждое рациональное число $x/y$ имеет представление египетской дроби, в котором наибольший знаменатель равен $O(y\log ^{2}y/\log \log y)$.

Согласно предположению Чжи-Вэй Сунь , сделанному в сентябре 2015 года , Каждое положительное рациональное число имеет представление египетской дроби, в котором каждый знаменатель является практическим числом. Гипотезу доказал Дэвид Эппштейн ( 2021 ).

Аналогии с простыми числами

Одна из причин интереса к практическим числам состоит в том, что многие из их свойств аналогичны свойствам простых чисел . Действительно, для практических чисел известны теоремы, аналогичные гипотезе Гольдбаха и гипотезе простых чисел-близнецов : каждое положительное четное целое число является суммой двух практических чисел, и существует бесконечно много троек практических чисел. $(x-2,x,x+2)$. Мелфи также показал что существует бесконечно много практических чисел Фибоначчи (последовательность A124105 в OEIS ); аналогичный вопрос о существовании бесконечного числа простых чисел Фибоначчи остается открытым. Хаусман и Шапиро (1984) показали, что в интервале всегда существует практическое число. $[x^{2},(x+1)^{2})]$ для любого положительного реального $x$, результат, аналогичный гипотезе Лежандра для простых чисел. Более того, для всех достаточно больших $x$, интервал $[x-x^{0.4872},x]$ содержит много практических чисел.

Позволять $p(x)$ посчитайте, сколько практических чисел не более $x$. Маргенштерн (1991) предположил, что $p(x)$ асимптотически $cx/\log x$ для некоторой константы $c$, формула, которая напоминает теорему о простых числах , усиливая более раннее утверждение Эрдеша и Локстона (1979) о том, что практические числа имеют нулевую плотность в целых числах.Улучшив оценку Тененбаума (1986) , Сайас (1997) обнаружил, что $p(x)$ имеет порядок величины $x/\log x$. Вайнгартнер (2015) доказал гипотезу Маргенштерна. У нас есть

$$p(x)={\frac {cx}{\log x}}\left(1+O\!\left({\frac {1}{\log x}}\right)\right),$$

где $c=1.33607...$ Таким образом, практических чисел примерно на 33,6% больше, чем простых чисел. Точное значение постоянного коэффициента $c$ дается

$$c={\frac {1}{1-e^{-\gamma }}}\sum _{n\ {\text{practical}}}{\frac {1}{n}}{\Biggl (}\sum _{p\leq \sigma (n)+1}{\frac {\log p}{p-1}}-\log n{\Biggr )}\prod _{p\leq \sigma (n)+1}\left(1-{\frac {1}{p}}\right),$$

где $\gamma$ – постоянная Эйлера–Машерони и $p$ пробегает простые числа.

Как и в случае с простыми числами в арифметической прогрессии, даны два натуральных числа. $a$ и $q$, у нас есть

$$|\{n\leq x:n{\text{ practical and }}n\equiv a{\bmod {q}}\}|={\frac {c_{q,a}x}{\log x}}+O_{q}\left({\frac {x}{(\log x)^{2}}}\right).$$

Постоянный фактор $c_{q,a}$ положительно тогда и только тогда, когда существует более одного практического числа, совпадающего с $a{\bmod {q}}$.Если $\gcd(q,a)=\gcd(q,b)$, затем $c_{q,a}=c_{q,b}$. Например, около 38,26% практических чисел имеют последнюю десятичную цифру 0, а последние цифры 2, 4, 6, 8 встречаются с одинаковой относительной частотой 15,43%.

Ссылки

• Эппштейн, Дэвид (2021), «Египетские дроби со знаменателями из последовательностей, замкнутых при удвоении» , Journal of Integer Sequences , 24 : 21.8.8, arXiv : 2109.12217
• Эрдеш, Пол ; Локстон, Дж. Х. (1979), «Некоторые проблемы в partitio numerorum», Журнал Австралийского математического общества, серия A , 27 (3): 319–331, doi : 10.1017/S144678870001243X .
• Хейворт, MR (1980), «Подробнее о панарифмических числах», New Zealand Math. Маг. , 17 (1): 24–28 . Цитируется Маргенштерном (1991) .
• Хаусман, Мириам; Шапиро, Гарольд Н. (1984), «О практических числах», Communications on Pure and Applied Mathematics , 37 (5): 705–713, doi : 10.1002/cpa.3160370507 , MR   0752596 .
• Маргенштерн, Морис (1984), «Результаты и предположения о практических числах», Comptes Rendus de l'Académie des Sciences, Série I , 299 (18): 895–898 . Цитируется Маргенштерном (1991) .
• Маргенштерн, Морис (1991), «Практические числа: теория, наблюдения и предположения», Journal of Number Theory , 37 (1): 1–36, doi : 10.1016/S0022-314X(05)80022-8 , MR   1089787 .
• Мелфи, Джузеппе (1995), «Обзор практических чисел», Rend. Сем. Мат. унив. Пол. Турин , 53 (4): 347–359 .
• Мелфи, Джузеппе (1996), «О двух гипотезах о практических числах», Journal of Number Theory , 56 (1): 205–210, doi : 10.1006/jnth.1996.0012 , MR   1370203 .
• Митринович, Драгослав С.; Шандор, Йожеф; Крстичи, Борислав (1996), «III.50 Практические числа», Справочник по теории чисел, Том 1 , Математика и ее приложения, том. 351, Kluwer Academic Publishers, стр. 118–119, ISBN.  978-0-7923-3823-9 .
• Померанс, К.; Вайнгартнер, А. (2021), «О простых и практических числах», Ramanujan Journal , 57 (3): 981–1000, arXiv : 2007.11062 , doi : 10.1007/s11139-020-00354-y , S2CID   220686445 .
• Робинсон, Д.Ф. (1979), «Египетские дроби с помощью греческой теории чисел», New Zealand Math. Маг. , 16 (2): 47–52 . Цитируется Маргенштерном (1991) и Митриновичем, Шандором и Крстичи (1996) .
• Сайас, Эрик (1997), «Целые числа в плотных делителях, I», Journal of Number Theory , 62 (1): 163–191, doi : 10.1006/jnth.1997.2057 , MR   1430008 .
• Сиглер, Лоуренс Э. (пер.) (2002), Liber Abaci Фибоначчи , Springer-Verlag, стр. 119–121, ISBN  0-387-95419-8 .
• Серпинский, Вацлав (1955), «О свойстве натуральных чисел», Annali di Matematica Pura ed Applicata , 39 (1): 69–74, doi : 10.1007/BF02410762 , S2CID   121592840 .
• Сринивасан, AK (1948), «Практические цифры» (PDF) , Current Science , 17 : 179–180, MR   0027799 , заархивировано из оригинала (PDF) 5 марта 2016 г.
• Стюарт, Б.М. (1954), «Суммы различных делителей», American Journal of Mathematics , 76 (4), The Johns Hopkins University Press: 779–785, doi : 10.2307/2372651 , JSTOR   2372651 , MR   0064800 .
• Тененбаум, Г. (1986), «О проблеме просеивания и ее приложениях», Ann. наук. Норм школа. Как дела. (4) , 19 (1): 1–30, doi : 10.24033/asens.1502 , MR   0860809 .
• Тененбаум, Г .; Йокота, Х. (1990), «Длина и знаменатели египетских дробей», Journal of Number Theory , 35 (2): 150–156, doi : 10.1016/0022-314X(90)90109-5 , MR   1057319 .
• Восе, М. (1985), «Египетские дроби», Бюллетень Лондонского математического общества , 17 (1): 21, doi : 10.1112/blms/17.1.21 , MR   0766441 .
• Вайнгартнер, А. (2015), «Практические числа и распределение делителей», The Quarterly Journal of Mathematics , 66 (2): 743–758, arXiv : 1405.2585 , doi : 10.1093/qmath/hav006 .
• Вайнгартнер, А. (2019), «О постоянном множителе в нескольких связанных асимптотических оценках», Mathematics of Computation , 88 (318): 1883–1902, arXiv : 1705.06349 , doi : 10.1090/mcom/3402 , S2CID   85532616 .
• Вайнгартнер, А. (2020), «Постоянный множитель в асимптотике практических чисел», International Journal of Number Theory , 16 (3): 629–638, arXiv : 1906.07819 , doi : 10.1142/S1793042120500311 , S2CID   195069356 .
• Вайнгартнер, А. (2021), «Расширение теоремы Зигеля-Вальфиса», Proceedings of the American Mathematical Society , 149 (11): 4699–4708, arXiv : 2011.06627 , doi : 10.1090/proc/15607 , S2CID   226956079 .
• Вайнгартнер, А. (2022), «Несколько гладкие числа в коротких интервалах», Ramanujan Journal , 60 (2): 447–453, arXiv : 2105.13568 , doi : 10.1007/s11139-022-00552-w , S2CID   235247868 .

Внешние ссылки

• Таблицы практических чисел. Архивировано 26 декабря 2017 г. на Wayback Machine, составлено Джузеппе Мелфи.
• Практическое число в PlanetMath .
• Вайсштейн, Эрик В. , «Практическое число» , MathWorld