Центрированное шестиугольное число
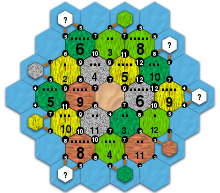
19 тайлов земли,
Всего 37 плиток
В математике и комбинаторике центрированное шестиугольное число , или шестнадцатеричное число , [1] [2] — это центрированное фигурное число , которое представляет собой шестиугольник с точкой в центре и всеми остальными точками, окружающими центральную точку в шестиугольной решетке . Следующие рисунки иллюстрируют такое расположение первых четырех центрированных шестиугольных чисел:
Центрированные шестиугольные числа не следует путать с угловыми шестиугольными числами , которые представляют собой фигурные числа, в которых связанные шестиугольники имеют общую вершину.
Последовательность шестиугольных чисел начинается следующим образом (последовательность A003215 в OEIS ):
Формула [ править ]

-е центрированное шестиугольное число n определяется формулой [2]
Выразив формулу как
показывает, что центрированное шестиугольное число для n в 1 более чем в 6 раз больше ( n − 1) -го треугольного числа .
В противоположном направлении индекс n соответствует центрированному шестиугольному числу. можно рассчитать по формуле
Это можно использовать в качестве проверки того, является ли число H центрированным шестиугольным: это будет тогда и только тогда, когда приведенное выше выражение является целым числом.
Повторение и производящая функция [ править ]
Центрированные шестиугольные числа удовлетворить рекуррентное соотношение [2]
Отсюда мы можем вычислить производящую функцию . Производящая функция удовлетворяет
Последний член представляет собой Тейлора ряд , поэтому мы получаем
и оказаться в
Свойства [ править ]
В системе счисления 10 можно заметить, что самые правые (наименее значащие) цифры шестиугольных чисел следуют порядку 1–7–9–7–1 (повторяется с периодом 5).Это следует из последней цифры чисел треугольника (последовательность A008954 в OEIS ), которые повторяют 0-1-3-1-0 при взятии по модулю 5.В системе счисления 6 самая правая цифра всегда равна 1: 1 6 , 11 6 , 31 6 , 101 6 , 141 6 , 231 6 , 331 6 , 441 6 ...Это следует из того, что каждое центрированное шестиугольное число по модулю 6 (=10 6 ) равно 1.
Сумма первых n центрированных шестиугольных чисел равна n 3 . То есть центрированные шестиугольные пирамидальные числа и кубы — это одни и те же числа, но представляют собой разные фигуры. Если смотреть с противоположной точки зрения, центрированные шестиугольные числа представляют собой разности двух последовательных кубов, так что центрированные шестиугольные числа являются гномонами кубов . (Геометрически это видно из диаграммы.) В частности, простым шестиугольные числа с центром являются кубинскими простыми числами .
Разница между (2 n ) 2 а n -е центрированное шестиугольное число — это число вида 3 n 2 + 3 n − 1 , а разница между (2 n − 1) 2 а n- ное центрированное шестиугольное число является проническим числом .
Приложения [ править ]

Многие с сегментированными зеркалами телескопы-отражатели имеют главные зеркала, состоящие из центрированного шестиугольного ряда сегментов (без учета удаления центрального сегмента для обеспечения прохождения света) для упрощения системы управления. [3] Некоторые примеры:
| Телескоп | Количество сегменты | Число отсутствующий | Общий | n-й центрированный шестиугольное число |
|---|---|---|---|---|
| Гигантский Магелланов телескоп | 7 | 0 | 7 | 2 |
| Космический телескоп Джеймса Уэбба | 18 | 1 | 19 | 3 |
| Большой телескоп Канарских островов | 36 | 1 | 37 | 4 |
| Гвидо Хорна д'Артуро Прототип | 61 | 0 | 61 | 5 |
| Южноафриканский большой телескоп | 91 | 0 | 91 | 6 |
Ссылки [ править ]
- ^ Хиндин, HJ (1983). «Звезды, шестиугольники, треугольные числа и тройки Пифагора». Дж. Рек. Математика . 16 : 191–193.
- ^ Jump up to: Перейти обратно: а б с Деза, Елена ; Деза, М. (2012). Образные числа . Всемирная научная. стр. 47–55. ISBN 978-981-4355-48-3 .
- ^ Маст, Т.С. и Нельсон, Дж. Э. Управление фигурой для сегментированного зеркала телескопа . США: Н.П., 1979. Интернет. дои: 10.2172/6194407.










