Элементарная арифметика

Символы для математических операций элементарного уровня. Слева вверху по часовой стрелке: сложение, деление, умножение и вычитание.

Элементарная арифметика — это раздел математики , включающий основные числовые операции, а именно сложение , вычитание , умножение и деление . Из-за низкого уровня абстракции , широкого спектра применения и положения в качестве основы всей математики элементарная арифметика обычно известна как первая отрасль математики, которую преподают в школах.

Цифры

Основная статья: Числовая цифра

Цифры используются для представления значения чисел в системе счисления . Наиболее часто используемые цифры — это арабские цифры от 0 до 9, которые считаются десятичными (по основанию 10). Индо -арабская система счисления является наиболее часто используемой системой счисления и представляет собой позиционную систему обозначений , используемую для представления чисел с использованием этих цифр. Однако используются и другие системы, такие как цифры Кактовик , обычно используемые в эскимосско-алеутских языках Аляски , Канады и Гренландии (основание 20) , двоичная система, используемая компьютерами (основание 2), и язык Telefol (основание 27). Иногда используются и другие непозиционные системы счисления, например, римские цифры . Недостатком непозиционных систем является то, что они обычно имеют наибольшее выразимое число.

Функция преемника и порядок

В элементарной арифметике преемником натурального числа (включая ноль ) является следующее натуральное число, которое является результатом добавления единицы к этому числу. Предшественником натурального числа (исключая ноль) является предыдущее натуральное число и результат , полученный вычитанием единицы из этого числа. Например, преемником нуля является единица, а предшественником одиннадцати — десять ( $0+1=1$ и $11-1=10$). Каждое натуральное число имеет преемника, и каждое натуральное число, кроме первого (ноль или 1), имеет предшественника.

Натуральные числа имеют полный порядок , то есть значения любых двух натуральных чисел можно сравнивать друг с другом. Если одно число больше ( $>$) другое число, то последнее меньше ( $<$) бывший. Например, три меньше восьми ( $3<8$), таким образом, восемь больше трех ( $8>3$). Натуральные числа также хорошо упорядочены , а это означает, что любое подмножество натуральных чисел имеет наименьший элемент.

Подсчет

Основная статья: Счет § Счет в математике

Подсчет предполагает присвоение натурального числа каждому объекту в наборе , начиная с единицы для первого объекта и увеличивая на единицу для каждого последующего объекта. Количество объектов в наборе — это счетчик, равный наибольшему натуральному числу, присвоенному объекту в наборе. Это количество также известно как мощность множества, содержащего такие объекты.

Подсчет также может быть процессом подсчета , процессом выставления отметки для каждого объекта в наборе.

Неформально, два набора имеют одинаковую мощность, если элементы обоих наборов могут быть сопоставлены взаимно однозначным соответствием. Например, набор из 4 яблок и еще один из 4 бананов имеют одинаковую мощность, поскольку каждому яблоку можно назначить банан, в котором не осталось фруктов.

Дополнение

Пример сложения с переносом . Черные числа — это сложение, зеленое число — перенос, а синее число — сумма. В самой правой цифре сложение 9 и 7 дает 16, перенося 1 в следующую пару цифр слева, делая ее сложение 1 + 5 + 2 = 8. Следовательно, сложение 59 + 27 дает результат 86. .

Основная статья: Дополнение

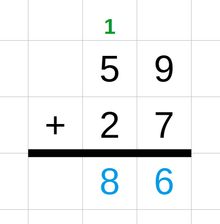
Сложение — это математическая операция, которая объединяет два или более чисел, называемых слагаемыми или слагаемыми, для получения объединенного числа, называемого суммой. Сложение двух чисел выражается знаком плюс ( $+$). Выполняется по следующим правилам:

• Сумма двух чисел равна числу, полученному сложением их отдельных значений.
• Порядок добавления слагаемых не влияет на сумму. Это известно как коммутативное свойство сложения. Например, (a + b) и (b + a) дадут одинаковый результат.
• Сумма двух чисел уникальна, то есть существует только один правильный ответ на сумму любых заданных чисел.
• Обратная операция сложения, называемая вычитанием, которую можно использовать для нахождения разницы между двумя или более числами.

Сложение используется в различных контекстах, включая сравнение количеств, объединение количеств и измерение. Когда сумма пары цифр дает двузначное число, цифра десятков в алгоритме сложения называется «цифрой переноса». При изучении элементарной арифметики учащиеся обычно учатся складывать целые числа , а также могут изучать такие темы, как отрицательные числа и дроби .

Вычитание

Основная статья: Вычитание

Вычитание используется для оценки разницы между двумя числами, где уменьшаемое — это число, из которого вычитается, а вычитаемое — это вычитаемое число. Обозначается знаком минус ( $-$). Знак минус также используется для обозначения отрицательных чисел, и их можно рассматривать как числа, вычтенные из 0.

Вычитание не является коммутативным, а это означает, что порядок чисел может изменить конечное значение; $3-5$ это не то же самое, что $5-3$. В элементарной арифметике уменьшаемое всегда больше вычитаемого, что дает положительный результат. Однако значения абсолютные $a-b$ и $b-a$ одинаковы ( $|a-b|=|b-a|$).

Вычитание также используется для разделения, объединения (например, определения размера подмножества определенного набора) и поиска величин в других контекстах. Например: «У Тома 8 яблок. Он отдает 3 яблока. Сколько у него осталось?» представляет собой разделение, а «У Тома 8 яблок. Три яблока зеленые, а остальные красные. Сколько красных?» представляет собой комбинацию . В некоторых случаях вычитание также можно использовать для определения общего количества объектов в группе, например: «У Тома было несколько яблок. Джейн дала ему еще 3 яблока, так что теперь у него 8 яблок. Со скольки он начал?»

Существует несколько методов выполнения вычитания. Традиционный математический метод учит учащихся начальной школы вычитать, используя методы, подходящие для ручного счета. Реформистская математика в целом отличается отсутствием предпочтения какой-либо конкретной техники, заменяющейся направляющими 2 ^nd - учащимся изобретать свои собственные методы вычислений, например, использовать свойства отрицательных чисел в случае TERC .

В настоящее время в американских школах преподают метод вычитания с использованием заимствований. который был известен и опубликован в учебниках до более широкого внедрения этого метода в американские учебные программы. В методе заимствования решается такая задача на вычитание, как $86-39$можно решить, заимствовав 10 из разряда десятков и прибавив их к разряду единиц, чтобы облегчить вычитание. Например, вычитание 9 из 6 предполагает заимствование 10 из разряда десятков, превращая задачу в $70+16-39$. Это обозначается перечеркиванием 8, написанием 7 над ней и 1 над 6. Эти отметки называются «костылями», которые были изобретены Уильямом А. Браунеллом , который использовал их в исследовании в ноябре 1937 года.

Австрийский метод, также известный как метод сложения, преподается в некоторых европейских странах и используется некоторыми американцами из предыдущих поколений. В отличие от предыдущего метода, заимствования не используются, хотя есть костыли, которые различаются в зависимости от страны. Метод сложения предполагает увеличение вычитаемого, а не уменьшение вычитаемого, как в методе заимствования. Это превращает предыдущую проблему в $(80+16)-(39+10)$. Маленькая цифра 1 отмечена под вычитаемой цифрой для напоминания.

Пример

При вычитании чисел 792 и 308, начиная со столбца единиц, 2 становится меньше 8. Используя метод заимствования, 10 заимствуется из 90, уменьшая 90 до 80. Добавление этого 10 к 2 меняет задачу на $12-8$, что равно 4.

	Сотни	Десятки	Единицы
		8	1 2
	7	9	2
−	3	0	8
			4

В столбце десятков разница между 80 и 0 равна 80.

	Сотни	Десятки	Единицы
		8	1 2
	7	9	2
−	3	0	8
		8	4

В столбце сотен разница между 700 и 300 равна 400.

	Сотни	Десятки	Единицы
		8	1 2
	7	9	2
−	3	0	8
	4	8	4

Результат:

$792-308=484$

Умножение

Основная статья: Умножение

Умножение – это математическая операция многократного сложения. При умножении двух чисел полученное значение является произведением. Умножаемые числа называются множимыми и множителями и вообще известны как множители. Например, если есть пять мешков, в каждом из которых по три яблока, и яблоки из всех пяти мешков помещены в пустой мешок, в пустом мешке будет 15 яблок. Это можно выразить так: «пять три равно пятнадцати», «пять три равно пятнадцати» или «пятнадцать — произведение пяти и трех».

Умножение обозначается знаком умножения (×), звездочкой (*), круглыми скобками () или точкой (⋅). Следовательно, утверждение «пять раз три равно пятнадцать» можно записать как « $5\times 3=15$", " $5\ast 3=15$", " $(5)(3)=15$", или " $5\cdot 3=15$". Знак умножения является наиболее часто используемым символом умножения. , тогда как обозначение звездочки чаще всего используется в языках программирования . В алгебре символ умножения можно опустить; например, $xy$ представляет $x\times y$.

В элементарной арифметике умножение удовлетворяет следующим свойствам :

• Коммутативность . Переключение порядка в товаре не меняет результат: $a\times b=b\times a$.
• Ассоциативность . Изменение порядка скобок в продукте не меняет результат: $a\times (b\times c)=(a\times b)\times c$.
• Дистрибутивность . Умножение распределяет над сложением: $a\times (b+c)=a\times b+a\times c$.
• Личность . Любое число, умноженное на 1, является самим собой, т. е. 1 является мультипликативным тождеством : $a\times 1=a$.
• Нуль . Любое число, умноженное на 0, равно 0, т.е. 0 — это ноль или поглощающий элемент : $a\times 0=0$.

В алгоритме умножения цифра десятков произведения пары цифр называется «цифрой переноса». Чтобы перемножить пару цифр с помощью таблицы, необходимо найти пересечение строки первой цифры и столбца второй цифры, в котором будет находиться произведение двух цифр. Большинство пар цифр при умножении дают двузначные числа.

Пример умножения однозначного коэффициента

Умножив 729 и 3, начиная со столбца единиц, произведение 9 и 3 составит 27. 7 записывается под столбцом единиц, а 2 записывается над столбцом десятков в качестве переносимой цифры.

	Сотни	Десятки	скрывать Единицы
		2
	7	2	9
×			3
			7

Произведение 2 и 3 равно 6, а цифра переноса добавляет 2 к 6, поэтому под столбцом десятков записывается 8.

	Сотни	Десятки	скрывать Единицы
	7	2	9
×			3
		8	7

Произведение 7 и 3 равно 21, и поскольку это последняя цифра, 2 не будет записываться как цифра переноса, а будет записываться рядом с 1.

	Сотни	Десятки	показывать Единицы
	7	2	9
×			3
2	1	8	7

Результат:

$3\times 729=2187$

Пример умножения многозначных коэффициентов

Умножив 789 и 345, начиная со столбца единиц, произведение 789 и 5 составит 3945.

	7	8	показывать 9
×	3	4	5
3	9	4	5

4 - это разряд десятков. Множитель равен 40, а не 4. Произведение 789 и 40 равно 31560.

		7	8	показывать 9
	×	3	4	5
	3	9	4	5
3	1	5	6	0

3 — это разряд сотен. Множитель равен 300. Произведение 789 и 300 равно 236700.

			7	8	показывать 9
		×	3	4	5
		3	9	4	5
	3	1	5	6	0
2	3	6	7	0	0

Добавляем все товары,

				7	8	показывать 9
×				3	4	5
			3	9	4	5
		3	1	5	6	0
+	2	3	6	7	0	0
	2	7	2	2	0	5

Результат:

$789\times 345=272205$

Дивизия

Основные статьи: Деление (математика) и Длинное деление

Деление — это арифметическая операция, обратная умножению .

В частности, учитывая число a и ненулевое число b , если другое число c , умноженное на b , равно a , то есть $c\times b=a$, то a, разделенное на b , равно c .

То есть: ${\frac {a}{b}}=c$. Например, ${\frac {6}{3}}=2$.

Число а называется делимым, b — делителем, а с — частным. Деление на ноль считается невозможным на элементарном арифметическом уровне и обычно игнорируется.

Деление можно отобразить, поместив делимое над делителем с горизонтальной линией, также называемой винкулом , между ними. Например, a , разделенное на b, записывается как:

${\frac {a}{b}}$

Устно это можно прочитать как « а делённое на б » или « а над б ».

Другой способ выразить деление в одной строке — написать делимое , затем косую черту , а затем делитель , как показано ниже:

$a/b$

Это обычный способ разделения в большинстве языков программирования .

В рукописном или типографском варианте используется косая черта (дробная косая черта), но делимое увеличивается, а делитель понижается:

a ⁄ b

Любую из этих форм можно использовать для отображения дроби . Обыкновенная дробь — это выражение деления, в котором делимое и делитель являются числами (хотя обычно их называют числителем и знаменателем ), и это не означает, что деление необходимо вычислять дальше.

Более простой способ показать деление — использовать обелис (÷) следующим образом:

$a\div b.$

В некоторых неанглоязычных культурах , " a, разделенное на b ", пишется a : b . Однако в английском языке двоеточие ограничивается понятием отношений (« a равно b »).

Два числа можно разделить на бумаге методом деления в столбики . Сокращенная версия длинного деления, короткое деление , также может использоваться для меньших делителей.

Менее систематический метод включает в себя концепцию разбиения на части , включающую вычитание большего количества кратных из частичного остатка на каждом этапе.

Чтобы разделить на дробь, можно просто умножить на обратную величину (поменяв местами верхнюю и нижнюю части) этой дроби. Например:

$\textstyle {5\div {1 \over 2}=5\times {2 \over 1}=5\times 2=10}$

$\textstyle {{2 \over 3}\div {2 \over 5}={2 \over 3}\times {5 \over 2}={10 \over 6}={5 \over 3}}$

Пример

Разделив 272 и 8, начиная с цифры сотен, 2 не делится на 8. Сложите 20 и 7, чтобы получить 27. Наибольшее число, на которое можно умножить делитель 8, не превышая 27, равно 3, поэтому цифра 3 записывается под столбцом десятков, чтобы начать построение частного. Вычитание 24 (произведение 3 и 8) из 27 дает в остатке 3 .

	2	7	показывать 2
÷			8
		3

8 обязательно больше остатка 3. Переходя к единицам для продолжения деления, получаем число 2. При сложении 30 и 2 получается 32, которое делится на 8, а частное 32 и 8 равно 4. Записывается 4. под столбцом «те».

	2	7	показывать 2
÷			8
		3	4

Результат:

$272\div 8=34$

Метод автобусной остановки

Еще один метод разделения, преподаваемый в некоторых школах, - это метод автобусных остановок, иногда обозначаемый как

          результат 
     (делитель) дивиденд 
 

Шаги показаны ниже на том же примере, что и выше:

     0  3  4   (Пояснения) 
     8|272 
       0  ( 8 ×  0  = 0) 
       2  7 ( 2 - 0 =  2  ) 
       24  ( 8 ×  3  = 24) 
        3  2 (27 - 24 =  3  ) 
        32  ( 8 ×  4  = 32) 
         0 (32 - 32 = 0) 
 

Заключение:

$272\div 8=34$

Образовательные стандарты

Элементарная арифметика обычно преподается на уровне начальной или средней школы и регулируется местными образовательными стандартами. В США и Канаде ведутся споры о содержании и методах обучения элементарной арифметике. Одной из проблем было использование калькуляторов вместо ручных вычислений, при этом некоторые утверждали, что для развития навыков ментальной арифметики использование калькуляторов должно быть ограничено. Другая дискуссия сосредоточилась на различии между традиционной математикой и реформистской математикой: традиционные методы часто больше сосредотачиваются на базовых вычислительных навыках, а методы реформирования уделяют больше внимания математическим концепциям более высокого уровня, таким как алгебра, статистика и решение задач.

В Соединенных Штатах стандарты Национального совета учителей математики 1989 года привели к изменению учебных программ начальной школы, в результате которого были уменьшены или опущены некоторые темы, традиционно считающиеся частью элементарной арифметики, в пользу большего внимания концепциям уровня колледжа. такие как алгебра и статистика . Этот сдвиг вызвал споры: некоторые утверждают, что он привел к отсутствию внимания к базовым вычислительным навыкам, которые важны для успеха на последующих уроках математики.

См. также

• Раннее умение считать
• Элементарная математика
• Дробление (деление)
• Знаки плюс и минус
• Аксиомы Пеано
• Деление на ноль
• Настоящий номер
• Мнимое число

Внешние ссылки

• «Дружеский подарок по науке арифметике» – арабский документ 15 века, в котором рассказывается об основах арифметики.