Кактовик цифры

См. также: Цифры Кактовик (блок Unicode)

Не путать с цифрами инупиак .

20 цифр системы Кактовик

или Цифры Кактовик цифры Кактовик-инупиак. — это с основанием 20, система числовых цифр созданная аляскинскими инупиатами . Они визуально знаковые , их формы обозначают отображаемое число.

В языке инупиаков используется двадцатеричная система счисления , как и в других эскимосско-алеутских языках Аляски и Канады (и бывшей Гренландии). Арабские цифры , разработанные для системы с основанием 10 , не подходят для инупиаков и других языков инуитов. Чтобы решить эту проблему, студенты в Кактовике, Аляска , в 1994 году изобрели систему записи чисел с основанием 20, которая распространилась среди аляскинских инупиатов и рассматривалась для использования в Канаде.

Система

См. Также: цифры инупиак

Инупиак , как и другие языки инуитов , имеет по основанию 20 систему счисления с подосновой 5 ( пятерично-десятеричная система). То есть количества подсчитываются в десятках (как в валлийском языке , а также в некоторых датских языках, таких как halvtreds «пятьдесят», и во французском языке, например quatre-vingts «восемьдесят»), с промежуточными цифрами для 5, 10 и 15. Таким образом, 78 определяется как три балла пятнадцать три .

Цифры Кактовика графически отражают лексическую структуру системы счисления инупиаков.

Двадцать цифр

0		Киситчисагвик	5		пять	10		десять	15		акимиак
1		атаусик	6		Ичаксрат	11		десять тысяч	16		Акимиак Атаусик
2		дом	7		пять	12		Кулит Малджук	17		Акимиак Малчук
3		пишасут	8		пять пять	13		десять пятнадцать	18		акимиак пять
4		четыре	9		кулинджутайчак	14		акимиагутаихак	19		инуинньягутаихак

Большие числа состоят из этих цифр в позиционной записи :

десятичный	Пятеричный
арабский	арабский	Кактовик
20	10 20
40	20 20
400	100 20
800	200 20

Ценности

В следующей таблице приведены десятичные значения цифр Кактовика до трех знаков слева и справа от места единиц.

Десятичные значения чисел Кактовика

н	п × 20 3	п × 20 2	п × 20 1	п × 20 0	п × 20 −1	п × 20 −2	п × 20 −3
1	, 8,000	400	20	1	. 0.05	. 0.0025	. 0.000 125
2	, 16,000	800	40	2	. 0.1	. 0.005	. 0.000 25
3	, 24,000	1,200	60	3	. 0.15	. 0.0075	. 0.000 375
4	, 32,000	1,600	80	4	. 0.2	. 0.01	. 0.000 5
5	, 40,000	2,000	100	5	. 0.25	. 0.0125	. 0.000 625
6	, 48,000	2,400	120	6	. 0.3	. 0.015	. 0.000 75
7	, 56,000	2,800	140	7	. 0.35	. 0.0175	. 0.000 875
8	, 64,000	3,200	160	8	. 0.4	. 0.02	. 0.001
9	, 72,000	3,600	180	9	. 0.45	. 0.0225	. 0.001 125
10	, 80,000	4,000	200	10	. 0.5	. 0.025	. 0.001 25
11	, 88,000	4,400	220	11	. 0.55	. 0.0275	. 0.001 375
12	, 96,000	4,800	240	12	. 0.6	. 0.03	. 0.001 5
13	, 104,000	5,200	260	13	. 0.65	. 0.0325	. 0.001 625
14	, 112,000	5,600	280	14	. 0.7	. 0.035	. 0.001 75
15	, 120,000	6,000	300	15	. 0.75	. 0.0375	. 0.001 875
16	, 128,000	6,400	320	16	. 0.8	. 0.04	. 0.002
17	, 136,000	6,800	340	17	. 0.85	. 0.0425	. 0.002 125
18	, 144,000	7,200	360	18	. 0.9	. 0.045	. 0.002 25
19	, 152,000	7,600	380	19	. 0.95	. 0.0475	. 0.002 375

Источник

Карта Аляски с указанием района Норт-Слоуп, части Инупиат Нунаат

Изучение цифр началось в 1994 году как дополнительное занятие, когда во время урока математики по изучению двоичных чисел в средней школе Гарольда Кавеолука на острове Бартер Кактовик , Аляска, Студенты отметили, что в их языке используется система с основанием 20.

Они обнаружили, что когда они пытались писать числа или выполнять арифметические действия с арабскими цифрами, им не хватало символов для представления чисел инупиак.

Сначала они решили этот недостаток, создав десять дополнительных символов, но обнаружили, что их трудно запомнить. В маленькой средней школе было всего девять учеников, поэтому вся школа могла работать вместе над созданием системы счисления с основанием 20. Их наставник Уильям Бартли руководил ими.

После мозгового штурма студенты пришли к выводу о нескольких качествах, которыми должна обладать идеальная система:

1. Визуальная простота: символы должны быть «легкими для запоминания».
2. Иконичность: должна быть «четкая связь между символами и их значениями».
3. Эффективность: символы должно «легко писать», и их можно «писать быстро», не отрывая карандаш от бумаги.
4. Отличительность: они должны «сильно отличаться от арабских цифр», чтобы не было путаницы между обозначениями в двух системах.
5. Эстетика: на них должно быть приятно смотреть.

В позиционной записи с основанием 20 число двадцать записывается цифрой 1, за которой следует цифра 0. В языке инупиак нет слова для обозначения нуля, и студенты решили, что кактовская цифра 0 должна выглядеть как скрещенные руки. это означает, что ничего не учитывается.

Когда ученики средней школы начали преподавать свою новую систему младшим школьникам, младшие ученики имели тенденцию сжимать числа, чтобы они поместились в блок того же размера. Таким образом, они создали знаковую систему обозначений, в которой основание из 5 образует верхнюю часть цифры, а остаток — нижнюю часть. Это оказалось визуально полезным при выполнении арифметики.

Вычисление

Счеты инупиак, предназначенные для использования с цифрами Кактовик.

Счеты

Учащиеся построили счеты с основанием 20. в школьной мастерской Первоначально они предназначались для облегчения преобразования десятичных чисел в двадцатеричные и наоборот, но студенты обнаружили, что их конструкция вполне естественно подходит для арифметики с двадцатеричным основанием. Верхняя часть их счетов имела по три бусины в каждом столбце для значений подосновы 5, а нижняя часть имела по четыре бусины в каждом столбце для остальных единиц.

Арифметика

Преимущество своей новой системы, которое студенты обнаружили, заключалось в том, что арифметика была проще, чем с арабскими цифрами. Сложение двух цифр будет выглядеть как их сумма. Например,

2 + 2 = 4

+ =

С вычитанием было еще проще: можно было просто посмотреть на число и убрать необходимое количество штрихов, чтобы получить ответ. Например,

4 − 1 = 3

− =

Еще одно преимущество заключалось в длинном делении . Визуальные аспекты и подбаза из пяти сделали длинное деление с большими дивидендами почти таким же простым, как и короткое деление, поскольку не требовалось записи в подтаблицах для умножения и вычитания промежуточных шагов. Учащиеся могли отслеживать штрихи промежуточных шагов цветными карандашами с помощью тщательно продуманной системы разбивки на фрагменты .

Примеры длинного деления

• 
  Простое длинное деление

  30,561 ₁₀

  3,Г81 ₂₀

  

  ÷

  ÷

  ÷

  61 ₁₀

  31 ₂₀

  

  =

  =

  =

  501 ₁₀

  151 ₂₀

  

  30,561₁₀ ÷ 61₁₀ = 501₁₀

  3,G81₂₀ ÷ 31₂₀ = 151₂₀

  ÷ =

  Делитель (черный) входит в первые две цифры делимого (фиолетовый) один раз, на единицу в частном (фиолетовый). Если повернуть, он вписывается в следующие две цифры (красный) один раз, поэтому следующая цифра в частном (красный) равна единице (пять). Последние две цифры сопоставляются один раз, образуя последнюю цифру в частном (синяя).
• 
  Длинное деление с большим количеством фрагментов

  46,349,226 ₁₀

  Е9Д,Д16 ₂₀

  

  ÷

  ÷

  ÷

  2,826 ₁₀

  716 ₂₀

  

  =

  =

  =

  16,401 ₁₀

  2,101 ₂₀

  

  46,349,226₁₀ ÷ 2,826₁₀ = 16,401₁₀

  E9D,D16₂₀ ÷ 716₂₀ = 2,101₂₀

  ÷ =

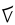
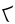  Делитель входит в первые три цифры делимого дважды (отмечено красным и синим), для двойки в частном (красный и синий), в следующие три раза (зеленый), не вписывается в следующие три цифры (таким образом, ноль в частном) и один раз помещается в оставшиеся розовые цифры.

Упрощенную таблицу умножения можно составить, найдя сначала произведения каждой базовой цифры, затем произведения оснований и подоснований и, наконец, произведение каждой подосновы:

×	1	2	3	4
1
2
3
4

×	1	2	3	4
5
10
15

×	5	10	15
5
10
15

Эти таблицы функционально полны для операций умножения с использованием числительных Кактовика, но для множителей как с основаниями, так и с подоснованиями необходимо предварительно их разъединить:

6 * 3 = 18

* = ( * ) + ( * ) =

В приведенном выше примере коэффициент В таблице встречается не уравнение (6), а его компоненты, (1) и (5), есть.

Наследие

Числа Кактовик получили широкое распространение среди инупиатов Аляски. Они были включены в программы языкового погружения и помогли возродить счет по основанию 20, который вышел из употребления среди инупиатов из-за преобладания системы по основанию 10 в школах с английским языком обучения.

Когда учащиеся средней школы «Кактовик», изобретшие эту систему, в 1995 году перешли в среднюю школу в Барроу, Аляска (теперь переименованную в Уткиагвик ), они взяли свое изобретение с собой. Им было разрешено преподавать эту математику учащимся местной средней школы, а местный колледж Икисавик добавил в свой каталог курс математики для инуитов.

В 1996 году Комиссия по истории языка и культуры инуитов официально приняла цифры: а в 1998 году Приполярный совет инуитов в Канаде рекомендовал разработать и использовать цифры Кактовик в этой стране.

Значение

Результаты Калифорнийского теста по математике в средней школе Кактовик в 1997 году значительно улучшились по сравнению с предыдущими годами. До введения новых цифр средний балл находился в 20-м процентиле; после их введения оценки выросли до уровня выше среднего по стране. Предполагается, что способность работать как с базой 10, так и с базой 20 может иметь сопоставимые преимущества с теми двуязычными студентами, которые имеют два способа мышления о мире.

Развитие местной системы счисления помогает продемонстрировать учащимся-уроженцам Аляски, что математика заложена в их культуре и языке, а не передана западной культурой. Это отход от ранее широко распространенного мнения, что математика была просто необходимостью для поступления в колледж или университет. Студенты-иностранцы могут увидеть практический пример иного мировоззрения, являющегося частью этноматематики .

В Юникоде

Основная статья: Цифры Кактовик (блок Юникода)

Цифры Кактовик были добавлены в стандарт Unicode в сентябре 2022 года с выпуском версии 15.0. Несколько шрифтов поддерживают этот блок.

Кактовик Цифры [1] [2] Официальная таблица кодов Консорциума Unicode (PDF)

0

1

2

3

4

5

6

7

8

9

А

Б

С

Д

И

Ф

U + 1D2Cx

𝋀

𝋁

𝋂

𝋃

𝋄

𝋅

𝋆

𝋇

𝋈

𝋉

𝋊

𝋋

𝋌

𝋍

𝋎

𝋏

U + 1D2Dx

𝋐

𝋑

𝋒

𝋓

Примечания 1. ^ Начиная с версии Unicode 15.1. 2. ^ Серые области обозначают неназначенные кодовые точки.

Графическое отображение цифр Кактовик
Официальная таблица кодов Консорциума Unicode (PDF)

	0	1	2	3	4	5	6	7	8	9	А	Б	С	Д	И	Ф
U + 1D2Cx
U + 1D2Dx

См. также

• Цифры майя , пятерично-десятеричная система из другой американской культуры.

Ссылки

• Бартли, У.М. Кларк (январь – февраль 1997 г.). «Старый путь имеет значение» (PDF) . Делимся своими путями . 2 (1): 12–13. Архивировано (PDF) из оригинала 25 июня 2013 г. Проверено 27 февраля 2017 г.
• Резолюция 89-09: Относительно цифр Кактовик . Приполярная конференция инуитов . Нуук, Гренландия . Июль 1998 г. Архивировано из оригинала 2 февраля 2017 г.
• Бартли, Уильям Кларк (2002). «Опираясь на традиции: числа инупиаков в школьной среде». В Хэнксе, Джудит Элейн; Фаст, Джеральд Р. (ред.). Перспективы коренных народов Северной Америки . Изменение лица математики. Рестон, Вирджиния: Национальный совет учителей математики. стр. 225–236. ISBN  978-0873535069 . Проверено 17 апреля 2024 г.
• Энгблом-Брэдли, Клодетт (2009). «Видеть математику индийскими глазами». В Уильямсе, Мария Шаа Тлаа (ред.). Читатель из числа коренных жителей Аляски: история, культура, политика . Издательство Университета Дьюка. стр. 237–245. дои : 10.1215/9780822390831-025 .
• Маклин, Эдна Ахгик (2012). Iñupiatun Uqaluit Taniktun Sivunniuġutiŋit [ Инупиак Северного склона в словаре английского языка ] (PDF) . Архивировано из оригинала (PDF) 10 декабря 2021 года.
• Маклин, Эдна Ахгик (2014). Инупиатун Укалуит Таниктун Сивунинит [ Инупиак-английский словарь ]. Издательство Университета Аляски. JSTOR   jj.1176788 .

Дальнейшее чтение

• Тиллингаст-Раби, Амори (июнь 2023 г.). «Система счисления, изобретенная школьниками-инуитами, дебютирует в Кремниевой долине» . Научный американский журнал . Проверено 13 апреля 2023 г.

Внешние ссылки

• Конвертер Кактовик – арабский язык , использующий изображения или Unicode
• Грюневальд, Эдгар (30 декабря 2019 г.). «Почему это лучшие цифры!» . Ютуб . Архивировано из оригинала 20 декабря 2021 года . Проверено 30 декабря 2019 г. Видео демонстрирует, насколько проще делить дольки с помощью интуитивно понятных цифр, таких как цифры «Кактовик»; иллюстрированные задачи были выбраны так, чтобы их было легко решить, как и задачи по знакомству ребенка с арифметикой.
• Сильва, Эдуардо Марин; Миллер, Кирк; Стрэнд, Кэтрин (29 апреля 2021 г.). «Запрос Unicode для цифр Кактовик (L2/21-058R)» (PDF) . Реестр документов Технического комитета Unicode . Проверено 30 апреля 2021 г.
• бесплатное приложение Kaktovik Calculator на iPhone (декабрь 2023 г.).