Бивектор

Параллельные плоские сегменты одинаковой ориентации и площади соответствуют одному и тому же бивектору a ∧ b .

В математике бивектор , или 2-вектор — это величина во внешней алгебре или геометрической алгебре которая расширяет идею скаляров и векторов . Если рассматривать скаляр как величину нулевой степени, а вектор как величину первой степени, то бивектор имеет вторую степень. Бивекторы находят применение во многих областях математики и физики. Они связаны с комплексными числами в двух измерениях, а также с псевдовекторами и векторными кватернионами в трех измерениях. Их можно использовать для создания вращений в пространстве любого количества измерений, и они являются полезным инструментом для классификации таких вращений.

Геометрически простой бивектор можно интерпретировать как характеризующий направленный сегмент плоскости , так же как векторы можно рассматривать как характеризующие направленные сегменты прямых . Бивектор a ∧ b имеет отношение (направление) плоскости, натянутой на a и b , имеет площадь, которая является скалярным кратным любого сегмента базовой плоскости с таким же отношением (а в геометрической алгебре он имеет величину , равную площадь параллелограмма с ребрами a и b ) и имеет ориентацию , соответствующую стороне a , на которой b лежит внутри плоскости, охватываемой a и b . С точки зрения непрофессионала, любая поверхность определяет один и тот же бивектор, если она параллельна одной и той же плоскости (то же самое положение), имеет одинаковую площадь и одинаковую ориентацию (см. Рисунок).

Бивекторы порождаются внешним произведением векторов: для двух векторов a и b их внешнее произведение a ∧ b является бивектором, как и любая сумма бивекторов. Не все бивекторы можно выразить как внешнее произведение без такого суммирования. называется бивектор, который можно выразить как внешнее произведение Точнее, простым ; в трех измерениях все бивекторы просты, но в более высоких измерениях это не так. Внешнее произведение двух векторов является чередующимся , поэтому a ∧ a — нулевой бивектор, а b ∧ a — отрицательный бивектор a ∧ b , создавая противоположную ориентацию. 2-го ранга Понятия, непосредственно связанные с бивектором, — это антисимметричный тензор и кососимметричная матрица .

История

Бивектор был впервые определен в 1844 году немецким математиком Германом Грассманом во внешней алгебре как результат внешнего произведения двух векторов. Буквально годом ранее в Ирландии Уильям Роуэн Гамильтон открыл кватернионы . Гамильтон придумал и вектор , и бивектор , последний в своих «Лекциях по кватернионам» (1853 г.), когда он ввел бикватернионы , имеют бивекторы векторные части которых . Только после того, как английский математик Уильям Кингдон Клиффорд в 1888 году добавил геометрическое произведение к алгебре Грассмана, включив в себя идеи Гамильтона и Грассмана, и основал алгебру Клиффорда , возник бивектор этой статьи. Генри Фордер использовал термин бивектор для разработки внешней алгебры в 1941 году.

В 1890-х годах Джозайя Уиллард Гиббс и Оливер Хевисайд разработали векторное исчисление , которое включало в себя отдельные перекрестные произведения и скалярные произведения , полученные в результате умножения кватернионов. Успех векторного исчисления и книги «Векторный анализ» Гиббса и Уилсона привел к тому, что идеи Гамильтона и Клиффорда долгое время игнорировались, поскольку большая часть математики и физики 20-го века была сформулирована в векторных терминах. Гиббс использовал векторы, чтобы выполнять роль бивекторов в трех измерениях, и использовал бивектор в смысле Гамильтона - использование, которое иногда копировалось. Сегодня бивектор в основном изучается как тема геометрической алгебры , алгебры Клиффорда над вещественными или комплексными векторными пространствами с квадратичной формой . Ее возрождение возглавил Дэвид Хестенс , который вместе с другими применил геометрическую алгебру к ряду новых приложений в физике .

Вывод

В этой статье бивектор будет рассматриваться только в реальных геометрических алгебрах, которые могут применяться в большинстве областей физики. Кроме того, если не указано иное, все примеры имеют евклидову метрику и, следовательно, положительно определенную квадратичную форму .

геометрическое

Бивектор возникает из определения геометрического произведения над векторным пространством с соответствующей квадратичной формой, иногда называемой метрикой . Для векторов a , b и c геометрическое произведение удовлетворяет следующим свойствам:

Ассоциативность

$(\mathbf {ab} )\mathbf {c} =\mathbf {a} (\mathbf {bc} )$

Левая и правая дистрибутивность

${\begin{aligned}\mathbf {a} (\mathbf {b} +\mathbf {c} )&=\mathbf {ab} +\mathbf {ac} \\(\mathbf {b} +\mathbf {c} )\mathbf {a} &=\mathbf {ba} +\mathbf {ca} \end{aligned}}$

Скалярный квадрат

$\mathbf {a} ^{2}=Q(\mathbf {a} )$, где Q — квадратичная форма, которая не обязательно должна быть положительно определенной .

Скалярное произведение

Из ассоциативности a ( ab ) = a ² b , является скаляром, умноженным на b . Когда b не параллелен и, следовательно, не является скалярным кратным a , ab не может быть скаляром. Но

${\tfrac {1}{2}}(\mathbf {ab} +\mathbf {ba} )={\tfrac {1}{2}}\left((\mathbf {a} +\mathbf {b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2}\right)$

представляет собой сумму скаляров и, следовательно, является скаляром. По закону косинусов в треугольнике, образованном векторами, его значение равно | а | | б | cos θ , где θ — угол между векторами. Следовательно, оно идентично скалярному произведению двух векторов и записывается так же:

$\mathbf {a} \cdot \mathbf {b} ={\tfrac {1}{2}}(\mathbf {ab} +\mathbf {ba} ).$

Он симметричен, имеет скалярные значения и может использоваться для определения угла между двумя векторами: в частности, если a и b ортогональны, произведение равно нулю.

Внешний вид изделия

Точно так же, как скалярное произведение можно сформулировать как симметричную часть геометрического произведения другой величины, внешнее произведение (иногда называемое «клиновым» или «прогрессивным» произведением) можно сформулировать как его антисимметричную часть :

$\mathbf {a} \wedge \mathbf {b} ={\tfrac {1}{2}}(\mathbf {ab} -\mathbf {ba} )$

Он антисимметричен по a и b.

$\mathbf {b} \wedge \mathbf {a} ={\tfrac {1}{2}}(\mathbf {ba} -\mathbf {ab} )=-{\tfrac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=-\mathbf {a} \wedge \mathbf {b}$

и дополнительно:

$\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} ={\tfrac {1}{2}}(\mathbf {ab} +\mathbf {ba} )+{\tfrac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=\mathbf {ab}$

То есть геометрическое произведение представляет собой сумму симметричного скалярного произведения и знакопеременного внешнего произведения.

Чтобы изучить природу a ∧ b , рассмотрим формулу

$(\mathbf {a} \cdot \mathbf {b} )^{2}-(\mathbf {a} \wedge \mathbf {b} )^{2}=\mathbf {a} ^{2}\mathbf {b} ^{2},$

что с использованием тригонометрического тождества Пифагора дает значение ( a ∧ b ) ²

$(\mathbf {a} \wedge \mathbf {b} )^{2}=(\mathbf {a} \cdot \mathbf {b} )^{2}-\mathbf {a} ^{2}\mathbf {b} ^{2}=\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}(\cos ^{2}\theta -1)=-\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta$

В случае отрицательного квадрата это не может быть скалярная или векторная величина, поэтому это новый тип объекта — бивектор . Он имеет величину | а | | б | | грех θ | , где θ — угол между векторами, поэтому для параллельных векторов он равен нулю.

Чтобы отличить их от векторов, бивекторы здесь пишутся жирными заглавными буквами, например:

$\mathbf {A} =\mathbf {a} \wedge \mathbf {b} =-\mathbf {b} \wedge \mathbf {a} \,,$

хотя используются и другие соглашения, в частности, поскольку векторы и бивекторы являются элементами геометрической алгебры.

Свойства

Алгебра, порожденная геометрическим произведением (то есть всеми объектами, образованными путем взятия повторяющихся сумм и геометрических произведений скаляров и векторов), является геометрической алгеброй над векторным пространством. Для евклидова векторного пространства эта алгебра записывается ${\mathcal {G}}_{n}$ или Cl _n ( R ) , где n — размерность векторного пространства R ^н . Cl _n ( R ) — это одновременно векторное пространство и алгебра, порожденная всеми произведениями векторов в R. ^н , поэтому он содержит все векторы и бивекторы. Точнее, как векторное пространство оно содержит векторы и бивекторы как линейные подпространства , но не как подалгебры (поскольку геометрическое произведение двух векторов обычно не является другим вектором).

Пространство ⋀ ² р ^н

Пространство всех бивекторов имеет размерность 1/2 n n ( и ) − 1 пишется ⋀ ² р ^н , и является второй внешней степенью исходного векторного пространства.

Даже подалгебра

Подалгебра, порожденная бивекторами, является четной подалгеброй геометрической алгебры, записываемой Cl ^[0]
_п ( р ) . Эта алгебра является результатом рассмотрения всех повторяющихся сумм и геометрических произведений скаляров и бивекторов. Он имеет размерность 2 ^{п -1} , и содержит ⋀ ² р ^н как линейное подпространство. В двух и трех измерениях четная подалгебра содержит только скаляры и бивекторы, и каждый из них представляет особый интерес. В двух измерениях четная подалгебра изоморфна комплексным числам C а в трех измерениях изоморфна кватернионам H. , она Четная подалгебра содержит вращения в любом измерении.

Величина

Как отмечалось в предыдущем разделе, величина простого бивектора, который является внешним произведением двух векторов a и b , равна | а | | б | sin θ , где θ — угол между векторами. Это написано | Б | , где B — бивектор.

Для обычных бивекторов величину можно рассчитать, взяв норму бивектора, рассматриваемого как вектор в пространстве ⋀ ² р ^н . Если величина равна нулю, то все компоненты бивектора равны нулю, а бивектор - это нулевой бивектор, который как элемент геометрической алгебры равен скалярному нулю.

Единичные бивекторы

Единичный бивектор — это единица величины. Такой бивектор можно получить из любого ненулевого бивектора, разделив бивектор на его величину, то есть

${\frac {\mathbf {B} }{\left\vert \mathbf {B} \right\vert }}.$

Особую полезность представляют единичные бивекторы, образованные из произведений стандартного базиса векторного пространства. Если e _i и e _j — разные базисные векторы, то произведение e _i ∧ e _j является бивектором. Поскольку e _i и e _j ортогональны, e _i ∧ e _j = e _i e _j , записанное e _ij , и имеет единичную величину, поскольку векторы являются единичными векторами . Множество всех бивекторов, полученных из базиса таким образом, образует основу для ⋀ ² р ^н . Например, в четырех измерениях основа для ⋀ ² р ⁴ это ( е ₁ е ₂ , е ₁ е ₃ , е ₁ е ₄ , е ₂ е ₃ , е ₂ е ₄ , е ₃ е ₄ ) или ( е ₁₂ , е ₁₃ , е ₁₄ , е ₂₃ , е ₂₄ , е ₃₄ ).

Простые бивекторы

Внешний продукт двух векторов является бивектором, но не все бивекторы являются внешними произведениями двух векторов. Например, в четырех измерениях бивектор

$\mathbf {B} =\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}=\mathbf {e} _{1}\mathbf {e} _{2}+\mathbf {e} _{3}\mathbf {e} _{4}=\mathbf {e} _{12}+\mathbf {e} _{34}$

не может быть записано как внешнее произведение двух векторов. Бивектор, который можно записать как внешнее произведение двух векторов, прост. В двух и трех измерениях все бивекторы просты, но не в четырех и более измерениях; в четырех измерениях каждый бивектор представляет собой сумму не более двух внешних произведений. Бивектор имеет действительный квадрат тогда и только тогда, когда он прост, и только простые бивекторы могут быть геометрически представлены направленной плоской областью.

Произведение двух бивекторов

Геометрическое произведение двух бивекторов A и B равно

$\mathbf {A} \mathbf {B} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} +\mathbf {A} \wedge \mathbf {B} .$

Величина A · B представляет собой скалярное произведение со скалярным знаком, а A ∧ B — это внешнее произведение степени 4, которое возникает в четырех или более измерениях. Величина A × B представляет собой бивекторное произведение коммутатора , определяемое формулой

$\mathbf {A} \times \mathbf {B} ={\tfrac {1}{2}}(\mathbf {AB} -\mathbf {BA} ),$

Пространство бивекторов ⋀ ² р ^н является алгеброй Ли над R с коммутаторным произведением в качестве скобки Ли. Полное геометрическое произведение бивекторов порождает четную подалгебру.

Особый интерес представляет произведение бивектора на самого себя. Поскольку произведение коммутатора антисимметрично, оно упрощается до

$\mathbf {A} \mathbf {A} =\mathbf {A} \cdot \mathbf {A} +\mathbf {A} \wedge \mathbf {A} .$

Если бивектор простой, последний член равен нулю, а произведение представляет собой скалярное значение A · A , которое можно использовать для проверки простоты. В частности, внешний продукт бивекторов существует только в четырех или более измерениях, поэтому все бивекторы в двух и трех измерениях просты.

Общие бивекторы и матрицы

Бивекторы изоморфны кососимметричным матрицам любого числа измерений. Например, общий бивектор B ₂₃ e ₂₃ + B ₃₁ e ₃₁ + B ₁₂ e ₁₂ в трех измерениях отображается в матрицу

$M_{B}={\begin{pmatrix}0&B_{12}&-B_{31}\\-B_{12}&0&B_{23}\\B_{31}&-B_{23}&0\end{pmatrix}}.$

Это, умноженное на векторы с обеих сторон, дает тот же вектор, что и произведение вектора и бивектора за вычетом внешнего произведения; примером является тензор угловой скорости .

Кососимметричные матрицы генерируют ортогональные матрицы с определителем 1 посредством экспоненциального отображения. В частности, применение экспоненциальной карты к бивектору, связанному с вращением, дает матрицу вращения . Матрица вращения M _R , заданная кососимметричной матрицей выше, равна

$M_{R}=\exp {M_{B}}.$

Вращение, описываемое M _R, такое же, как вращение, описываемое ротором R , определяемым формулой

$R=\exp {{\tfrac {1}{2}}B},$

и матрица M _R также может быть рассчитана непосредственно из ротора R . В трех измерениях это определяется выражением

$M_{R}={\begin{pmatrix}(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{1}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{2}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{3}\end{pmatrix}}.$

Бивекторы связаны с собственными значениями матрицы вращения. Учитывая матрицу вращения M, собственные значения можно вычислить, решив характеристическое уравнение для этой матрицы 0 = det( M − λI ) . По основной теореме алгебры оно имеет три корня (из которых только один действительный, поскольку имеется только один собственный вектор, т. е. ось вращения). Остальные корни должны быть комплексно-сопряженной парой. Они имеют единичную величину, то есть чисто мнимые логарифмы, равные величине бивектора, связанного с вращением, который также является углом поворота. Собственные векторы, связанные с комплексными собственными значениями, находятся в плоскости бивектора, поэтому внешнее произведение двух непараллельных собственных векторов дает бивектор (или его кратное число).

Два измерения

обычно записывают При работе с координатами в геометрической алгебре базисные векторы как ( e ₁ , e ₂ , ...) — это соглашение будет использоваться здесь.

Вектор в реальном двумерном пространстве R ² можно записать a = a ₁ e ₁ + a ₂ e ₂ , где a ₁ и a ₂ — действительные числа, e ₁ и e ₂ — ортонормированные базисные векторы. Геометрическое произведение двух таких векторов равно

${\begin{aligned}\mathbf {a} \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2})\\&=a_{1}b_{1}\mathbf {e} _{1}\mathbf {e} _{1}+a_{1}b_{2}\mathbf {e} _{1}\mathbf {e} _{2}+a_{2}b_{1}\mathbf {e} _{2}\mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\mathbf {e} _{2}\\&=a_{1}b_{1}+a_{2}b_{2}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}$

Его можно разделить на симметричное скалярное произведение и антисимметричное внешнее произведение с бивекторным знаком:

${\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2},\\\mathbf {a} \wedge \mathbf {b} &=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}$

Все бивекторы в двух измерениях имеют эту форму, то есть кратны бивектору e ₁ e ₂ , записанному e ₁₂ , чтобы подчеркнуть, что это бивектор, а не вектор. Величина e ₁₂ равна 1 , при этом

$\mathbf {e} _{12}^{2}=-1,$

поэтому он называется единичным бивектором . Термин «единичный бивектор» можно использовать в других измерениях, но он однозначно определен (с точностью до знака) только в двух измерениях, и все бивекторы кратны e ₁₂ . Элементом высшего класса алгебры e ₁₂ также является псевдоскаляр , которому присвоен символ i .

Комплексные числа

Благодаря свойствам отрицательного квадрата и единичной величины единичный бивектор можно отождествить с мнимой единицей комплексных чисел . Бивекторы и скаляры вместе образуют четную подалгебру геометрической алгебры, которая изоморфна комплексным числам C . Четная подалгебра имеет базис (1, e ₁₂ ) , вся алгебра имеет базис (1, e ₁ , e ₂ , e ₁₂ ) .

Комплексные числа обычно отождествляются с координатными осями и двумерными векторами, что означало бы их сопоставление с векторными элементами геометрической алгебры. В этом нет противоречия, поскольку для перехода от общего вектора к комплексному числу необходимо идентифицировать ось как действительную ось, , е ₁ скажем . Это умножается на все векторы, чтобы сгенерировать элементы четной подалгебры.

Все свойства комплексных чисел можно вывести из бивекторов, но два из них представляют особый интерес. Во-первых, как и в случае с комплексными числами, произведения бивекторов и четная подалгебра коммутативны . Это верно только в двух измерениях, поэтому свойства бивектора в двух измерениях, зависящие от коммутативности, обычно не распространяются на более высокие измерения.

Во-вторых, можно записать общий бивектор

$\theta \mathbf {e} _{12}=i\theta ,$

где θ — действительное число. Помещая это в ряд Тейлора для экспоненциального отображения и используя свойство e ₁₂ ² = −1 приводит к бивекторной версии формулы Эйлера ,

$\exp {\theta \mathbf {e} _{12}}=\exp {i\theta }=\cos {\theta }+i\sin {\theta },$

который при умножении на любой вектор поворачивает его на угол θ относительно начала координат:

$(x'\mathbf {e} _{1}+y'\mathbf {e} _{2})=(x\mathbf {e} _{1}+y\mathbf {e} _{2})\exp {i\theta }.$

Произведение вектора на бивектор в двух измерениях антикоммутативно , поэтому все следующие произведения генерируют одинаковое вращение.

$\mathbf {v} '=\mathbf {v} \exp {i\theta }=\exp(-i\theta )\,\mathbf {v} =\exp({-i\theta }/{2})\,\mathbf {v} \exp({i\theta }/{2}).$

Из них последний продукт обобщается на более высокие измерения. Необходимое количество называется ротором и обозначается символом R , поэтому в двух измерениях ротор, который вращается на угол θ, можно записать

$R=\exp({-{\tfrac {1}{2}}i\theta })=\exp({-{\tfrac {1}{2}}\theta \mathbf {e} _{12}}),$

и вращение, которое он генерирует, равно

$\mathbf {v} '=R\mathbf {v} R^{-1}.$

Три измерения

В трех измерениях геометрическое произведение двух векторов равно

${\begin{aligned}\mathbf {ab} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})\\&=a_{1}b_{1}{\mathbf {e} _{1}}^{2}+a_{2}b_{2}{\mathbf {e} _{2}}^{2}+a_{3}b_{3}{\mathbf {e} _{3}}^{2}+(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{2}\mathbf {e} _{3}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{3}\mathbf {e} _{1}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}$

Его можно разделить на симметричное скалярное произведение и антисимметричное внешнее произведение с бивекторным знаком:

${\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\\\mathbf {a} \wedge \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{31}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}$

В трех измерениях все бивекторы просты и, следовательно, являются результатом внешнего продукта. Единичные бивекторы e ₂₃ , e ₃₁ и e ₁₂ образуют основу пространства бивекторов ⋀ ² р ³ , которое само по себе является трехмерным линейным пространством. Итак, если общий бивектор:

$\mathbf {A} =A_{23}\mathbf {e} _{23}+A_{31}\mathbf {e} _{31}+A_{12}\mathbf {e} _{12},$

их можно добавлять как векторы

$\mathbf {A} +\mathbf {B} =(A_{23}+B_{23})\mathbf {e} _{23}+(A_{31}+B_{31})\mathbf {e} _{31}+(A_{12}+B_{12})\mathbf {e} _{12}.$

а при умножении они дают следующее

$\mathbf {A} \mathbf {B} =-A_{23}B_{23}-A_{31}B_{31}-A_{12}B_{12}+(A_{12}B_{31}-A_{31}B_{12})\mathbf {e} _{23}+(A_{23}B_{12}-A_{12}B_{23})\mathbf {e} _{31}+(A_{31}B_{23}-A_{23}B_{31})\mathbf {e} _{12}$

который можно разделить на симметричную скалярную и антисимметричную бивекторную части следующим образом:

${\begin{aligned}\mathbf {A} \cdot \mathbf {B} &=-A_{12}B_{12}-A_{31}B_{31}-A_{23}B_{23}\\\mathbf {A} \times \mathbf {B} &=(A_{23}B_{31}-A_{31}B_{23})\mathbf {e} _{12}+(A_{12}B_{23}-A_{23}B_{12})\mathbf {e} _{13}+(A_{31}B_{12}-A_{12}B_{31})\mathbf {e} _{23}.\end{aligned}}$

Внешний продукт двух бивекторов в трех измерениях равен нулю.

Бивектор B можно записать как произведение его величины и единичного бивектора, поэтому записывая β вместо | Б | и используя ряд Тейлора для экспоненциального отображения, можно показать, что

$\exp {\mathbf {B} }=\exp({\beta {\frac {\mathbf {B} }{\beta }}})=\cos {\beta }+{\frac {\mathbf {B} }{\beta }}\sin {\beta }.$

Это еще одна версия формулы Эйлера, но с общим трехмерным бивектором. В отличие от двухмерных измерений, бивекторы не являются коммутативными, поэтому свойства, зависящие от коммутативности, не применяются в трех измерениях. Например, в общем случае exp( A + B ) ≠ exp( A ) exp( B ) в трех (или более) измерениях.

Полная геометрическая алгебра в трех измерениях Cl ₃ ( R ) имеет базис ( 1 , e ₁ , e ₂ , e ₃ , e ₂₃ , e ₃₁ , e ₁₂ , e ₁₂₃ ). Элемент e ₁₂₃ является тривектором и псевдоскаляром геометрии. Бивекторы в трех измерениях иногда отождествляют с псевдовекторами. с которыми они связаны, как обсуждается ниже .

Кватернионы

Бивекторы не замкнуты относительно геометрического произведения, а четная подалгебра замкнута. В трех измерениях он состоит из всех скалярных и бивекторных элементов геометрической алгебры, поэтому общий элемент можно записать, например, a + A , где a — скалярная часть, а A — бивекторная часть. написано кл. ^[0]
₃ и имеет базис (1, e ₂₃ , e ₃₁ , e ₁₂ ) . Произведение двух общих элементов четной подалгебры есть

$(a+\mathbf {A} )(b+\mathbf {B} )=ab+a\mathbf {B} +b\mathbf {A} +\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .$

Четная подалгебра, то есть алгебра, состоящая из скаляров и изоморфна кватернионам бивекторов H . , сравнив базис с базисом кватерниона или с приведенным выше произведением, которое идентично произведению кватернионов, за исключением изменения знака, которое относится к отрицательным произведениям в бивекторном скалярном произведении A · B. В этом можно убедиться , Другие свойства кватернионов могут быть аналогичным образом связаны с геометрической алгеброй или получены из нее.

Это говорит о том, что обычное разделение кватерниона на скалярную и векторную части лучше представить как разделение на скалярную и бивекторную части; если это будет сделано, произведение кватернионов станет просто геометрическим произведением. Он также связывает кватернионы в трех измерениях с комплексными числами в двух измерениях, поскольку каждое из них изоморфно четной подалгебре для этого измерения, и это отношение распространяется на более высокие измерения.

Вектор вращения

Вектор вращения, полученный из представления вращения по оси и углу , представляет собой компактный способ представления вращения в трех измерениях. В своей наиболее компактной форме он состоит из вектора, произведения единичного вектора ω , который является осью вращения на (знаковый) угол поворота θ , так что величина общего вектора вращения θω равна (беззнаковому) угол поворота.

Кватернион, связанный с вращением, равен

$q=\left(\cos {{\tfrac {1}{2}}\theta },\omega \sin {{\tfrac {1}{2}}\theta }\right)$

В геометрической алгебре вращение представлено бивектором. Это можно увидеть в отношении к кватернионам. Пусть Ω — единичный бивектор в плоскости вращения, и пусть θ — угол поворота . Тогда бивектор вращения равен Ω θ . Кватернион близко соответствует экспоненте половины бивектора Ω θ . То есть компоненты кватерниона соответствуют скалярной и бивекторной частям следующего выражения:

$$\exp {{\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta }=\cos {{\tfrac {1}{2}}\theta }+{\boldsymbol {\Omega }}\sin {{\tfrac {1}{2}}\theta }$$

Экспоненту можно определить через ее степенной ряд и легко оценить, используя тот факт, что Ω в квадрате равен −1 .

Таким образом, вращения могут быть представлены бивекторами. Так же, как кватернионы являются элементами геометрической алгебры, они связаны экспоненциальным отображением в этой алгебре.

Роторы

Бивектор Ω θ генерирует вращение по экспоненциальному отображению. Генерируемые четные элементы вращают общий вектор в трех измерениях так же, как кватернионы:

$$\mathbf {v} '=\exp(-{\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta )\,\mathbf {v} \exp({\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta ).$$

Как и в двух измерениях, величина exp(− 1/2 ​ ​ Ω θ ) называется ротором и R. пишется Величина exp( 1 / 2 Ω θ ) тогда R ⁻¹ , и они генерируют вращения как

$$\mathbf {v} '=R\mathbf {v} R^{-1}.$$

Это идентично двухмерному, за исключением того, что роторы представляют собой четырехмерные объекты, изоморфные кватернионам. Это можно обобщить на все измерения с помощью роторов, элементов четной подалгебры с единичной величиной, создаваемых экспоненциальной картой из бивекторов. Они образуют двойное покрытие над группой вращения, поэтому роторы R и − R представляют одно и то же вращение.

Осевые векторы

3-угловой момент как бивектор (плоский элемент) и аксиальный вектор частицы массы m с мгновенным 3-положением x и 3-импульсом p .

Вектор вращения является примером осевого вектора . Осевые векторы, или псевдовекторы, представляют собой векторы с той особенностью, что их координаты претерпевают изменение знака относительно обычных векторов (также называемых «полярными векторами») при инверсии через начало координат, отражении в плоскости или другом линейном преобразовании, изменяющем ориентацию. . Примеры включают такие величины, как крутящий момент , угловой момент и векторные магнитные поля . Величины, которые использовали бы осевые векторы в векторной алгебре , правильно представляются бивекторами в геометрической алгебре. Точнее, если выбрана основная ориентация, аксиальные векторы естественным образом отождествляются с обычными векторами; дает тогда двойственный Ходжу изоморфизм между осевыми векторами и бивекторами, поэтому каждый осевой вектор связан с бивектором, и наоборот; то есть

$\mathbf {A} ={\star }\mathbf {a} \,,\quad \mathbf {a} ={\star }\mathbf {A}$

где ${\star }$— звезда Ходжа. Обратите внимание, что если основная ориентация меняется на противоположную путем инверсии через начало координат, как отождествление осевых векторов с обычными векторами, так и двойственный знак Ходжа меняют знак, но бивекторы не сдвигаются с места. Альтернативно, используя единичный псевдоскаляр в Cl ₃ ( R ) , i = e ₁ e ₂ e ₃ дает

$\mathbf {A} =\mathbf {a} i\,,\quad \mathbf {a} =-\mathbf {A} i.$

Это проще в использовании, поскольку продукт представляет собой просто геометрический продукт. Но он антисимметричен, потому что (как и в двух измерениях) единичный псевдоскаляр i квадратично равен −1 , поэтому в одном из произведений необходим отрицательный результат.

Эта связь распространяется на такие операции, как векторное векторное произведение и внешнее произведение с бивекторным знаком, поскольку, если они записаны в виде определителей, они вычисляются одинаково:

$\mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{1}&\mathbf {e} _{2}&\mathbf {e} _{3}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,\quad \mathbf {a} \wedge \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{23}&\mathbf {e} _{31}&\mathbf {e} _{12}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,$

так связаны двойственностью Ходжа:

${\star }(\mathbf {a} \wedge \mathbf {b} )=\mathbf {a\times b} \,,\quad {\star }(\mathbf {a\times b} )=\mathbf {a} \wedge \mathbf {b} \,.$

Бивекторы имеют ряд преимуществ перед аксиальными векторами. Они лучше устраняют неоднозначность аксиальных и полярных векторов, то есть величин, представленных ими, поэтому становится яснее, какие операции разрешены и каковы их результаты. Например, внутреннее произведение полярного вектора и аксиального вектора, полученное в результате векторного произведения в тройном произведении, должно привести к псевдоскаляру , результат, который более очевиден, если вычисление оформлено как внешнее произведение вектора и бивектора. Они распространяются на другие измерения; в частности, бивекторы можно использовать для описания таких величин, как крутящий момент и угловой момент, как в двух, так и в трех измерениях. Кроме того, они во многом соответствуют геометрической интуиции, как показано в следующем разделе.

Геометрическая

Параллельные плоские сегменты одинаковой ориентации и площади соответствуют одному и тому же бивектору a ∧ b .

Как следует из их названия и названия алгебры, одной из привлекательных сторон бивекторов является то, что они имеют естественную геометрическую интерпретацию. Это можно описать в любом измерении, но лучше всего это делать в трех измерениях, где можно провести параллели с более знакомыми объектами, прежде чем применять их к более высоким измерениям. В двух измерениях геометрическая интерпретация тривиальна, поскольку пространство двумерно и имеет только одну плоскость, и с ней связаны все бивекторы, отличающиеся только масштабным коэффициентом.

Все бивекторы можно интерпретировать как плоскости или, точнее, как направленные плоские сегменты. В трех измерениях бивектор имеет три свойства, которые можно интерпретировать геометрически:

• Расположение плоскости в пространстве, а именно положение плоскости (или, альтернативно, вращение , геометрическая ориентация или градиент плоскости), связано с соотношением компонентов бивектора. В частности, три базисных бивектора, e ₂₃ , e ₃₁ и e ₁₂ , или их скалярные кратные, связаны с плоскостью yz , плоскостью zx и плоскостью xy соответственно.
• Величина бивектора связана с площадью плоского сегмента. Область не имеет определенной формы, поэтому можно использовать любую форму. Его даже можно представить другими способами, например, с помощью угловой меры. Но если векторы интерпретируются как длины, бивектор обычно интерпретируется как площадь с теми же единицами измерения, как показано ниже.
• Подобно направлению вектора, плоскость , связанная с бивектором, имеет направление, циркуляцию или чувство вращения в плоскости, которое принимает два значения, видимых как по часовой стрелке и против часовой стрелки, если смотреть с точки зрения, а не в плоскости. Это связано со сменой знака бивектора, то есть при изменении направления на противоположное бивектор инвертируется. С другой стороны, если два бивектора имеют одинаковое положение и величину, но противоположные направления, то один из них является отрицательным по отношению к другому.
• Если представить его в виде параллелограмма с началом векторов в 0, то площадь со знаком является определителем декартовых координат векторов ( a _x b _y − b _x a _y ).

Перекрестное a × b ортогонально b бивектору a ∧ . произведение

В трех измерениях все бивекторы могут быть созданы внешним произведением двух векторов. Если бивектор B = a ∧ b , то величина B равна

$|\mathbf {B} |=|\mathbf {a} ||\mathbf {b} |\sin \theta ,$

где θ — угол между векторами. Это площадь параллелограмма с ребрами a и b , как показано на рисунке. Одна из интерпретаций состоит в том, что область сметается b при движении вдоль a . Внешний продукт антисимметричен, поэтому изменение порядка a и b для перемещения вдоль b приводит к образованию бивектора с противоположным направлением, которое является отрицательным по отношению к первому. Плоскость бивектора a ∧ b содержит как a , так и b , поэтому они оба параллельны плоскости.

Бивекторы и аксиальные векторы связаны двойственностью Ходжа . В реальном векторном пространстве двойственный вектор Ходжа связывает подпространство с его ортогональным дополнением , поэтому, если бивектор представлен плоскостью, то связанный с ним осевой вектор является просто нормалью к поверхности плоскости . Плоскость имеет две нормали, по одной с каждой стороны, что дает две возможные ориентации плоскости и бивектора.

Связь между силой F , крутящим моментом τ , линейным моментом p угловым моментом L. и

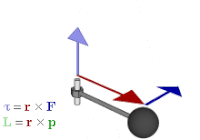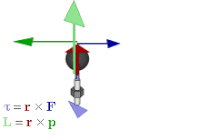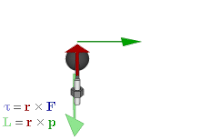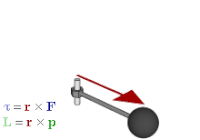
Это связывает перекрестное произведение с внешним произведением . Его также можно использовать для представления физических величин, таких как крутящий момент и угловой момент . В векторной алгебре они обычно представляются векторами, перпендикулярными плоскости силы , линейного импульса или смещения, из которых они рассчитываются. Но если вместо этого используется бивектор, то плоскость является плоскостью бивектора, и это более естественный способ представления величин и того, как они действуют. В отличие от векторного представления, оно также обобщается на другие измерения.

Произведение двух бивекторов имеет геометрическую интерпретацию. Для ненулевых бивекторов A и B произведение можно разбить на симметричную и антисимметричную части следующим образом:

$\mathbf {AB} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .$

Как и векторы, они имеют величины | А · Б | = | А | | Б | потому что θ и | А × Б | = | А | | Б | sin θ , где θ — угол между плоскостями. В трех измерениях он такой же, как угол между векторами нормалей, двойственными плоскостям, и в некоторой степени обобщается в более высоких измерениях.

Два бивектора, две непараллельные стороны призмы, добавляются, чтобы получить третий бивектор.

Бивекторы можно объединять в области. Учитывая два ненулевых бивектора B и C в трех измерениях, всегда можно найти вектор, который содержится в обоих, скажем , поэтому бивекторы можно записать как внешние произведения, включающие :

${\begin{aligned}\mathbf {B} &=\mathbf {a} \wedge \mathbf {b} \\\mathbf {C} &=\mathbf {a} \wedge \mathbf {c} \end{aligned}}$

Это можно интерпретировать геометрически, как показано на диаграмме: сумма двух площадей дает третью, причем три области образуют грани призмы с a , b , c и b + c в качестве ребер. Это соответствует двум способам расчета площади с использованием распределения внешнего произведения:

${\begin{aligned}\mathbf {B} +\mathbf {C} &=\mathbf {a} \wedge \mathbf {b} +\mathbf {a} \wedge \mathbf {c} \\&=\mathbf {a} \wedge (\mathbf {b} +\mathbf {c} ).\end{aligned}}$

Это работает только в трех измерениях, поскольку это единственное измерение, где должен существовать вектор, параллельный обоим бивекторам. В более высоких измерениях бивекторы обычно не связаны с одной плоскостью, или, если они являются (простыми бивекторами), два бивектора могут не иметь общего вектора и, таким образом, в сумме давать непростой бивектор.

Четыре измерения

В четырех измерениях базовые элементы пространства ⋀ ² р ⁴ бивекторов ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ), поэтому общий бивектор имеет вид

$\mathbf {A} =a_{12}\mathbf {e} _{12}+a_{13}\mathbf {e} _{13}+a_{14}\mathbf {e} _{14}+a_{23}\mathbf {e} _{23}+a_{24}\mathbf {e} _{24}+a_{34}\mathbf {e} _{34}.$

Ортогональность

В четырех измерениях двойственный бивектору Ходжа является бивектором, а пространство ⋀ ² р ⁴ двойственна сама себе. Нормальные векторы не уникальны, вместо этого каждая плоскость ортогональна всем векторам в своем дуальном пространстве Ходжа. Это можно использовать для разделения бивекторов на две «половинки» следующим образом. У нас есть три пары ортогональных бивекторов: ( e ₁₂ , e ₃₄ ) , ( e ₁₃ , e ₂₄ ) и ( e ₁₄ , e ₂₃ ) . Существует четыре различных способа выбора одного бивектора из каждой из первых двух пар, и как только эти первые два выбраны, их сумма дает третий бивектор из другой пары. Например, ( е ₁₂ , е ₁₃ , е ₁₄ ) и ( е ₂₃ , е ₂₄ , е ₃₄ ) .

Простые бивекторы в 4D

В четырех измерениях бивекторы генерируются внешним произведением векторов из R. ⁴ , но с одним важным отличием от R ³ и Р ² . В четырех измерениях не все бивекторы просты. Существуют бивекторы, такие как e ₁₂ + e ₃₄ , которые не могут быть порождены внешним произведением двух векторов. Это также означает, что у них нет реального, то есть скалярного, квадрата. В этом случае

$(\mathbf {e} _{12}+\mathbf {e} _{34})^{2}=\mathbf {e} _{12}\mathbf {e} _{12}+\mathbf {e} _{12}\mathbf {e} _{34}+\mathbf {e} _{34}\mathbf {e} _{12}+\mathbf {e} _{34}\mathbf {e} _{34}=-2+2\mathbf {e} _{1234}.$

Элемент e ₁₂₃₄ является псевдоскаляром в Cl ₄ , отличным от скаляра, поэтому квадрат нескалярен.

Все бивекторы в четырех измерениях могут быть созданы с использованием не более двух внешних произведений и четырех векторов. Приведенный выше бивектор можно записать как

$\mathbf {e} _{12}+\mathbf {e} _{34}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}.$

Аналогично каждый бивектор можно записать как сумму двух простых бивекторов. Для этого полезно выбрать два ортогональных бивектора, и это всегда можно сделать. Более того, для общего бивектора выбор простых бивекторов единственен, т. е. существует только один способ разложения на ортогональные бивекторы; единственным исключением является случай, когда два ортогональных бивектора имеют равные величины (как в приведенном выше примере): в этом случае разложение не уникально. В случае простых бивекторов разложение всегда уникально, с дополнительным бонусом, заключающимся в том, что одна из ортогональных частей равна нулю.

Вращения в R ⁴

Как и в трех измерениях, бивекторы в четырех измерениях генерируют вращения посредством экспоненциальной карты, и все вращения могут быть созданы таким образом. Как и в трех измерениях, если B — бивектор, то ротор R — exp. 1/2 B вращения и генерируются таким же образом:

$v'=RvR^{-1}.$

Трехмерная проекция тессеракта, совершающего изоклиническое вращение .

Однако генерируемые вращения более сложны. Их можно классифицировать следующим образом:

Простые вращения - это те, которые фиксируют плоскость в 4D и поворачивают на угол «около» этой плоскости.

двойные вращения имеют только одну фиксированную точку, начало координат, и вращаются на два угла вокруг двух ортогональных плоскостей. В общем случае углы разные, а плоскости заданы однозначно.

изоклинические вращения - это двойные вращения, при которых углы поворота равны. В этом случае плоскости, вокруг которых происходит вращение, не единственны.

Они генерируются бивекторами простым способом. Простые вращения генерируются простыми бивекторами, при этом фиксированная плоскость двойственна или ортогональна плоскости бивектора. Можно сказать, что вращение происходит вокруг этой плоскости, в плоскости бивектора. Все остальные бивекторы генерируют двойное вращение, причем два угла поворота равны величинам двух простых бивекторов, из которых состоит непростой бивектор. Изоклинические вращения возникают, когда эти величины равны, и в этом случае разложение на два простых бивектора не однозначно.

Бивекторы вообще не коммутируют, за исключением ортогональных бивекторов и их показателей. Таким образом, если бивектор B = B ₁ + B ₂ , где B ₁ и B ₂ — ортогональные простые бивекторы, используется для создания вращения, он разлагается на два простых вращения, которые коммутируют следующим образом:

$R=\exp({\tfrac {1}{2}}(\mathbf {B} _{1}+\mathbf {B} _{2}))=\exp({\tfrac {1}{2}}\mathbf {B} _{1})\,\exp({\tfrac {1}{2}}\mathbf {B} _{2})=\exp({\tfrac {1}{2}}\mathbf {B} _{2})\,\exp({\tfrac {1}{2}}\mathbf {B} _{1})$

Это всегда возможно сделать, поскольку все бивекторы можно выразить как суммы ортогональных бивекторов.

Вращение пространства-времени

Пространство-время — это математическая модель нашей Вселенной, используемая в специальной теории относительности. Оно состоит из трех пространственных измерений и одного временного измерения, объединенных в единое четырехмерное пространство. Это естественно описывается с помощью геометрической алгебры и бивекторов с евклидовой метрики заменой метрикой Минковского . Эта алгебра идентична алгебре евклидова пространства, за исключением того, что сигнатура изменена, поэтому

$\mathbf {e} _{i}^{2}={\begin{cases}1,&i=1,2,3\\-1,&i=4\end{cases}}$

(Обратите внимание, что порядок и индексы, приведенные выше, не являются универсальными — здесь e ₄ — времяподобное измерение). Геометрическая алгебра — это Cl _3,1 ( R ) , а подпространство бивекторов — ⋀ ² р ^3,1 .

Простые бивекторы бывают двух типов. Простые бивекторы e ₂₃ , e ₃₁ и e ₁₂ имеют отрицательные квадраты и охватывают бивекторы трехмерного подпространства, соответствующего евклидову пространству, R ³ . Эти бивекторы порождают обычные вращения в R ³ .

Простые бивекторы e ₁₄ , e ₂₄ и e ₃₄ имеют положительные квадраты и как плоскости охватывают пространственное измерение и временное измерение. Они также генерируют вращения через экспоненциальную карту, но вместо тригонометрических функций необходимы гиперболические функции, которые генерируют ротор следующим образом:

$\exp {{\tfrac {1}{2}}{{\boldsymbol {\Omega }}\theta }}=\cosh {{\tfrac {1}{2}}\theta }+{\boldsymbol {\Omega }}\sinh {{\tfrac {1}{2}}\theta },$

где Ω — бивектор ( e ₁₄ и т. д.), отождествляемый через метрику с антисимметричным линейным преобразованием R ^3,1 . Это бусты Лоренца , выраженные особенно компактным образом, с использованием той же алгебры, что и в R ³ и Р ⁴ .

В общем, все вращения пространства-времени генерируются из бивекторов посредством экспоненциального отображения, то есть общий ротор, порожденный бивектором A , имеет форму

$R=\exp {{\tfrac {1}{2}}\mathbf {A} }.$

Совокупность всех вращений в пространстве-времени образует группу Лоренца , и из них можно вывести большинство следствий специальной теории относительности. В более общем плане это показывает, как преобразования в евклидовом пространстве и пространстве-времени могут быть описаны с использованием одной и той же алгебры.

Уравнения Максвелла

(Примечание: в этом разделе традиционные 3-векторы обозначены линиями над символами и вектором пространства-времени, а бивекторы - жирными символами, причем векторы J и A исключительно в верхнем регистре)

Уравнения Максвелла используются в физике для описания взаимосвязи между электрическими и магнитными полями. Обычно задаваемые в виде четырех дифференциальных уравнений, они имеют особенно компактную форму, когда поля выражаются в виде бивектора пространства-времени из ⋀ ² р ^3,1 . Если электрическое и магнитное поля в R ³ E , и B то электромагнитный бивектор равен

$\mathbf {F} ={\frac {1}{c}}{\overline {E}}\mathbf {e} _{4}+{\overline {B}}\mathbf {e} _{123},$

где e ₄ — это снова базисный вектор времениподобного измерения, а c — скорость света . Произведение B e ₁₂₃ дает бивектор, который является двойственным по Ходжу к B в трех измерениях, как обсуждалось выше , в то время как E e ₄ как произведение ортогональных векторов также имеет бивекторное значение. В целом это электромагнитный тензор, более компактно выражаемый как бивектор, и используемый следующим образом. Во-первых, это связано с 4-током J , векторной величиной, определяемой формулой

$\mathbf {J} ={\overline {j}}+c\rho \mathbf {e} _{4},$

где j — плотность тока , а ρ — плотность заряда . Они связаны дифференциальным оператором ∂, который

$\partial =\nabla -\mathbf {e} _{4}{\frac {1}{c}}{\frac {\partial }{\partial t}}.$

Оператор ∇ — дифференциальный оператор в геометрической алгебре, действующий на размерности пространства и определяемый формулой ∇ M = ∇· M + ∇∧ M . Применительно к векторам ∇· M представляет собой дивергенцию , а ∇∧ M представляет собой ротор , но с бивектором, а не векторным результатом, который в трех измерениях двойственен ротору. Для общей величины M они действуют как понижающие и повышающие дифференциальные операторы. В частности, если M является скаляром, то этот оператор является просто градиентом , и его можно рассматривать как геометрическо-алгебраический del оператор .

Вместе их можно использовать для придания особенно компактной формы уравнениям Максвелла с источниками:

$\partial \mathbf {F} =\mathbf {J} .$

Это уравнение, разложенное в соответствии с геометрической алгеброй с использованием геометрических произведений, которые оказывают как повышение, так и понижение оценок, эквивалентно четырем уравнениям Максвелла. Это также связано с электромагнитным четырехпотенциалом , вектором A , заданным формулой

$\mathbf {A} ={\overline {A}}+{\frac {1}{c}}V\mathbf {e} _{4},$

где A — векторный магнитный потенциал, а V — электрический потенциал. Он связан с электромагнитным бивектором следующим образом

$\partial \mathbf {A} =-\mathbf {F} ,$

используя тот же дифференциальный оператор ∂ .

Высшие измерения

Как было предложено в предыдущих разделах, большая часть геометрической алгебры хорошо обобщается на более высокие измерения. Геометрическая алгебра для вещественного пространства R ^н есть Cl _n ( R ) , а подпространство бивекторов есть ⋀ ² р ^н .

Количество простых бивекторов, необходимых для формирования общего бивектора, увеличивается с увеличением размерности, поэтому для нечетного n это ( n - 1)/2 , для четного n это n / 2 . Таким образом, для четырех и пяти измерений необходимы только два простых бивектора, а для шести и семи измерений — три. Например, в шести измерениях со стандартным базисом ( e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ ) бивектор

$\mathbf {e} _{12}+\mathbf {e} _{34}+\mathbf {e} _{56}$

есть сумма трёх простых бивекторов, но не меньше. Как и в четырех измерениях, для этой суммы всегда можно найти ортогональные простые бивекторы.

Вращения в высших измерениях

Как и в трехмерном, и в четырехмерном измерениях, роторы генерируются экспоненциальной картой, поэтому

$\exp {{\tfrac {1}{2}}\mathbf {B} }$

— ротор, порожденный B. бивектором Простые вращения, которые происходят в плоскости вращения вокруг неподвижного лезвия размером ( n - 2) , генерируются простыми бивекторами, в то время как другие бивекторы генерируют более сложные вращения, которые можно описать в терминах простых бивекторов, суммами которых они являются. каждый из которых связан с плоскостью вращения. Все бивекторы могут быть выражены как сумма ортогональных и коммутативных простых бивекторов, поэтому вращения всегда можно разложить на набор коммутативных вращений вокруг плоскостей, связанных с этими бивекторами. Группа роторов в n измерениях — это группа спиновая Spin( n ) .

Одна примечательная особенность, связанная с количеством простых бивекторов и, следовательно, плоскостей вращения, заключается в том, что в нечетных измерениях каждое вращение имеет фиксированную ось - неправильно называть ее осью вращения, поскольку в более высоких измерениях вращения происходят в нескольких плоскостях, ортогональных. к этому. Это связано с бивекторами, поскольку бивекторы в нечетных измерениях разлагаются на такое же количество бивекторов, что и четное измерение ниже, поэтому имеют такое же количество плоскостей, но одно дополнительное измерение. Поскольку каждая плоскость генерирует вращение в двух измерениях в нечетных измерениях, должно быть одно измерение, то есть ось, которое не вращается.

Бивекторы также связаны с матрицей вращения в n измерениях. Как и в трех измерениях, характеристическое уравнение матрицы можно решить, чтобы найти собственные значения . В нечетных измерениях он имеет один действительный корень с собственным вектором на фиксированной оси, а в четных измерениях он не имеет действительных корней, поэтому либо все корни, либо все, кроме одного, представляют собой комплексно-сопряженные пары. Каждой паре соответствует простая компонента бивектора, связанная с вращением. В частности, логарифм каждой пары представляет собой величину с точностью до знака, а собственные векторы, генерируемые из корней, параллельны и поэтому могут использоваться для создания бивектора. В общем случае собственные значения и бивекторы уникальны, а набор собственных значений дает полное разложение на простые бивекторы; если корни повторяются, то разложение бивектора на простые бивекторы неоднозначно.

Проективная геометрия

применить к проективной геометрии Геометрическую алгебру можно напрямую . Используемая геометрическая алгебра — Cl _n ( R ), n ≥ 3 , алгебра вещественного векторного пространства R. ^н . Это используется для описания объектов в реальном проективном пространстве RP. ^{п -1} . Ненулевые векторы в Cl _n ( R ) или R ^н связаны с точками в проективном пространстве, поэтому векторы, которые отличаются только масштабным коэффициентом, поэтому их внешнее произведение равно нулю, отображаются в одну и ту же точку. Ненулевые простые бивекторы в ⋀ ² р ^н представлять линии в RP ^{п -1} , при этом бивекторы различаются только масштабным коэффициентом (положительным или отрицательным), представляющим одну и ту же линию.

Описание проективной геометрии можно построить в геометрической алгебре с помощью основных операций. Например, учитывая две различные точки в RP ^{п -1} представлены векторами a и b, содержащая их строка имеет вид a ∧ b (или b ∧ a ). Две прямые пересекаются в точке, если A ∧ B = 0 для их бивекторов A и B . Эта точка задается вектором

$\mathbf {p} =\mathbf {A} \lor \mathbf {B} =(\mathbf {A} \times \mathbf {B} )J^{-1}.$

Операция « ∨ » — это встреча, которую можно определить, как указано выше, в терминах соединения: J = A ∧ B. для ненулевого A ∧ B . С помощью этих операций проективную геометрию можно сформулировать в терминах геометрической алгебры. Например, для третьего (ненулевого) бивектора C точка p лежит на прямой, заданной C тогда и только тогда, когда

$\mathbf {p} \land \mathbf {C} =0.$

Таким образом, условие линий, заданных A , B и C коллинеарности , равно

$(\mathbf {A} \lor \mathbf {B} )\land \mathbf {C} =0,$

который в Cl ₃ ( R ) и RP ² упрощается до

$\langle \mathbf {ABC} \rangle =0,$

где угловые скобки обозначают скалярную часть геометрического произведения. Точно так же все операции с проективным пространством можно записать в терминах геометрической алгебры, где бивекторы представляют общие линии в проективном пространстве, поэтому всю геометрию можно разработать с использованием геометрической алгебры.

Тензоры и матрицы

Как отмечалось выше, бивектор может быть записан как кососимметричная матрица, которая посредством экспоненциального отображения генерирует матрицу вращения, описывающую то же вращение, что и ротор, также сгенерированное экспоненциальным отображением, но примененное к вектору. Но он также используется с другими бивекторами, такими как тензор угловой скорости и электромагнитный тензор , соответственно, кососимметричная матрица или тензор 3×3 и 4×4.

Настоящие бивекторы в ⋀ ² р ^н изоморфны кососимметричным матрицам размера n × n или, альтернативно, антисимметричным тензорам степени 2 на R ^н . Хотя бивекторы изоморфны векторам (посредством двойственности) в трех измерениях, они могут быть представлены кососимметричными матрицами в любом измерении. Это полезно для связи бивекторов с проблемами, описываемыми матрицами, чтобы их можно было переформулировать в терминах бивекторов, учитывая геометрическую интерпретацию, а затем часто решать их проще или геометрически связывать с другими бивекторными задачами.

В более общем смысле, каждая реальная геометрическая алгебра изоморфна матричной алгебре . Они содержат бивекторы в качестве подпространства, хотя часто это не особенно полезно. Эти матрицы представляют интерес главным образом как способ классификации алгебр Клиффорда.

См. также

• Диадики
• Многовекторный
• Полилинейная алгебра

Общие ссылки

• Дорст, Лео; Фонтейн, Дэниел; Манн, Стивен (2009). «§ 2.3.3 Визуализация бивекторов» . Геометрическая алгебра для информатики: объектно-ориентированный подход к геометрии (2-е изд.). Морган Кауфманн. п. 31 и далее . ISBN  978-0-12-374942-0 .
• Уитни, Хасслер (1957). Геометрическая теория интегрирования . Принстон: Издательство Принстонского университета . ISBN  978-0-486-44583-0 .
• Лунесто, Пертти (2001). Алгебры Клиффорда и спиноры . Кембридж: Издательство Кембриджского университета . ISBN  978-0-521-00551-7 .
• Крис Доран и Энтони Ласенби (2003). «§ 1.6 Внешний продукт» . Геометрическая алгебра для физиков . Кембридж: Издательство Кембриджского университета . п. 11 и далее . ISBN  978-0-521-71595-9 .