Тензор угловой скорости

Тензор угловой скорости представляет собой кососимметричную матрицу, определяемую формулой:

$\Omega ={\begin{pmatrix}0&-\omega _{z}&\omega _{y}\\\omega _{z}&0&-\omega _{x}\\-\omega _{y}&\omega _{x}&0\\\end{pmatrix}}$

Приведенные выше скалярные элементы соответствуют вектора угловой скорости. компонентам ${\boldsymbol {\omega }}=(\omega _{x},\omega _{y},\omega _{z})$.

Это бесконечно малая матрица вращения .Линейное отображение Ω действует как векторное произведение $({\boldsymbol {\omega }}\times )$:

${\boldsymbol {\omega }}\times {\boldsymbol {r}}=\Omega {\boldsymbol {r}}$

где ${\boldsymbol {r}}$ является вектором положения .

При умножении на разницу во времени получается тензор углового смещения .

Расчет тензора угловой скорости вращающейся системы отсчета

Вектор $\mathbf {r}$ равномерное круговое движение вокруг фиксированной оси удовлетворяет:

${\frac {d\mathbf {r} }{dt}}={\boldsymbol {\omega }}\times \mathbf {r} =\Omega \mathbf {r}$

Позволять $A(t)=[\mathbf {e} _{1}(t)\ \mathbf {e} _{2}(t)\ \mathbf {e} _{3}(t)]$ — матрица ориентации кадра, столбцы которой $\mathbf {e} _{1}$, $\mathbf {e} _{2}$, и $\mathbf {e} _{3}$ — движущиеся ортонормированные координатные векторы кадра. Мы можем получить тензор угловой скорости Ω ( t ) A ( t ) следующим образом:

Угловая скорость $\omega$ должно быть одинаковым для каждого из векторов-столбцов $\mathbf {e} _{i}$, поэтому мы имеем:

$${\begin{aligned}{\frac {dA}{dt}}&={\begin{bmatrix}{\dfrac {d\mathbf {e} _{1}}{dt}}&{\dfrac {d\mathbf {e} _{2}}{dt}}&{\dfrac {d\mathbf {e} _{3}}{dt}}\end{bmatrix}}\\&={\begin{bmatrix}\omega \times \mathbf {e} _{1}&\omega \times \mathbf {e} _{2}&\omega \times \mathbf {e} _{3}\end{bmatrix}}\\&={\begin{bmatrix}\Omega \mathbf {e} _{1}&\Omega \mathbf {e} _{2}&\Omega \mathbf {e} _{3}\end{bmatrix}}\\&=\Omega A,\end{aligned}}$$

что справедливо, даже если A ( t ) не вращается равномерно. Следовательно, тензор угловой скорости равен:

$\Omega ={\frac {dA}{dt}}A^{-1}={\frac {dA}{dt}}A^{\mathsf {T}},$

поскольку обратная ортогональная матрица $A$ это транспонирование $A^{\mathsf {T}}$.

Характеристики

См. Также: Бесконечно малое вращение

В общем случае угловая скорость в n -мерном пространстве является производной по времени тензора угловых смещений, который представляет собой кососимметричный тензор второго ранга .

Этот тензор Ω будет иметь n ( n −1)/2 независимых компонентов, что является размерностью алгебры Ли группы Ли вращений . -мерного пространства n внутреннего произведения

Двойственность относительно вектора скорости

В трех измерениях угловая скорость может быть представлена ​​псевдовектором, поскольку тензоры второго ранга двойственны псевдовекторам в трех измерениях. Поскольку тензор угловой скорости Ω = Ω ( t ) является кососимметричной матрицей :

$\Omega ={\begin{pmatrix}0&-\omega _{z}&\omega _{y}\\\omega _{z}&0&-\omega _{x}\\-\omega _{y}&\omega _{x}&0\\\end{pmatrix}},$

его двойник Ходжа - это вектор, который в точности соответствует предыдущему вектору угловой скорости. ${\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]$.

Экспонента Ом

Если мы знаем начальную систему отсчета A (0) и нам задан постоянный тензор угловой скорости Ω , мы можем получить A ( t ) для любого заданного t . Напомним матричное дифференциальное уравнение:

${\frac {dA}{dt}}=\Omega \cdot A.$

Это уравнение можно проинтегрировать и получить:

$A(t)=e^{Wt}A(0),$

что показывает связь с Ли группой вращений .

Ω кососимметричен

Доказано, что тензор угловой скорости кососимметричен , т.е. $\Omega ={\frac {dA(t)}{dt}}\cdot A^{\text{T}}$ удовлетворяет $\Omega ^{\text{T}}=-\Omega$.

Матрица вращения A ортогональна и обратна своей транспонированной, поэтому мы имеем $I=A\cdot A^{\text{T}}$. Для $A=A(t)$ матрица кадра, взяв производную уравнения по времени, дает:

$0={\frac {dA}{dt}}A^{\text{T}}+A{\frac {dA^{\text{T}}}{dt}}$

Применение формулы $(AB)^{\text{T}}=B^{\text{T}}A^{\text{T}}$,

$0={\frac {dA}{dt}}A^{\text{T}}+\left({\frac {dA}{dt}}A^{\text{T}}\right)^{\text{T}}=\Omega +\Omega ^{\text{T}}$

Таким образом, Ω является отрицательным выражением своего транспонирования, что означает, что оно кососимметрично.

Бескоординатное описание

В любой момент $t$тензор угловой скорости представляет собой линейную карту между вектором положения $\mathbf {r} (t)$ и векторы скорости $\mathbf {v} (t)$ точки на твердом теле, вращающейся вокруг начала координат:

$\mathbf {v} =\Omega \mathbf {r} .$

Связь между этой линейной картой и псевдовектором угловой скорости ${\boldsymbol {\omega }}$ заключается в следующем.

Поскольку Ω является производной ортогонального преобразования , билинейная форма

$B(\mathbf {r} ,\mathbf {s} )=(\Omega \mathbf {r} )\cdot \mathbf {s}$

является кососимметричным . Таким образом, мы можем применить тот факт внешней алгебры , что существует единственная линейная форма $L$ на $\Lambda ^{2}V$ что

$L(\mathbf {r} \wedge \mathbf {s} )=B(\mathbf {r} ,\mathbf {s} )$

где $\mathbf {r} \wedge \mathbf {s} \in \Lambda ^{2}V$ является продуктом внешним $\mathbf {r}$ и $\mathbf {s}$.

Взяв острую букву L ^♯ из L мы получаем

$(\Omega \mathbf {r} )\cdot \mathbf {s} =L^{\sharp }\cdot (\mathbf {r} \wedge \mathbf {s} )$

Представляем ${\boldsymbol {\omega }}:={\star }(L^{\sharp })$, как двойственное по Ходжу L ^♯ и дважды применив определение двойственного Ходжа, полагая, что предпочтительный единичный 3-вектор равен $\star 1$

$(\Omega \mathbf {r} )\cdot \mathbf {s} ={\star }({\star }(L^{\sharp })\wedge \mathbf {r} \wedge \mathbf {s} )={\star }({\boldsymbol {\omega }}\wedge \mathbf {r} \wedge \mathbf {s} )={\star }({\boldsymbol {\omega }}\wedge \mathbf {r} )\cdot \mathbf {s} =({\boldsymbol {\omega }}\times \mathbf {r} )\cdot \mathbf {s} ,$

где

${\boldsymbol {\omega }}\times \mathbf {r} :={\star }({\boldsymbol {\omega }}\wedge \mathbf {r} )$

по определению.

Потому что $\mathbf {s}$ — произвольный вектор, из невырожденности скалярного произведения следует

$\Omega \mathbf {r} ={\boldsymbol {\omega }}\times \mathbf {r}$

Угловая скорость как векторное поле

Поскольку тензор угловой скорости вращения твердого тела (в его системе покоя) представляет собой линейное преобразование, которое отображает положения в скорости (внутри твердого тела), его можно рассматривать как постоянное векторное поле . В частности, угловая скорость вращения представляет собой векторное поле Киллинга, принадлежащее элементу алгебры Ли SO(3) трехмерной группы вращения SO(3) .

Также можно показать, что векторное поле угловой скорости вращения составляет ровно половину ротора векторного поля линейной скорости v ( r ) твердого тела. В символах,

${\boldsymbol {\omega }}={\frac {1}{2}}\nabla \times \mathbf {v}$

Соображения относительно твердого тела

См. также: соглашения об осях

Положение точки P, расположенной в твердом теле (показано синим цветом). R _i представляет собой положение относительно лабораторного каркаса с центром в точке O , а r _i представляет собой положение относительно каркаса твердого тела с центром в точке O ′ . Начало системы координат твердого тела находится в позиции вектора R от лабораторной системы координат.

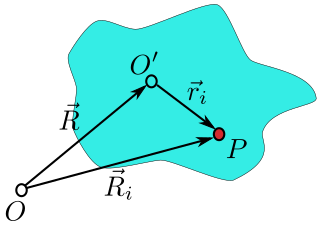
Те же уравнения для угловой скорости можно получить, рассуждая над вращающимся твердым телом . Здесь не предполагается, что твердое тело вращается вокруг начала координат. Вместо этого можно предположить, что он вращается вокруг произвольной точки, движущейся с линейной скоростью V ( t ) в каждый момент времени.

Для получения уравнений удобно представить твердое тело, закрепленное на шпангоутах, и рассмотреть систему координат, неподвижную относительно твердого тела. Затем мы изучим преобразования координат между этой координатой и фиксированной лабораторной системой отсчёта .

Как показано на рисунке справа, начало координат лабораторной системы находится в точке O начало координат системы твердого тела — в точке O ’ , а вектор от O до O ’ — это R. , Частица ( i ) в твердом теле расположена в точке P, и векторное положение этой частицы равно R _i в лабораторной системе отсчета и в позиции r _i в системе координат тела. Видно, что положение частицы можно записать:

$\mathbf {R} _{i}=\mathbf {R} +\mathbf {r} _{i}$

Определяющей характеристикой твердого тела является то, что расстояние между любыми двумя точками твердого тела не меняется во времени. Это означает, что длина вектора $\mathbf {r} _{i}$ неизменен. По теореме Эйлера о вращении мы можем заменить вектор $\mathbf {r} _{i}$ с ${\mathcal {R}}\mathbf {r} _{io}$ где ${\mathcal {R}}$ 3×3 представляет собой матрицу вращения и $\mathbf {r} _{io}$ — это положение частицы в некоторый фиксированный момент времени, скажем, t = 0 . Эта замена полезна, потому что теперь это только матрица вращения ${\mathcal {R}}$ который меняется во времени, а не опорный вектор $\mathbf {r} _{io}$, поскольку твердое тело вращается вокруг точки O ′ . Кроме того, поскольку три столбца матрицы вращения представляют три версора системы отсчета, вращающейся вместе с твердым телом, любое вращение вокруг любой оси теперь становится видимым, а вектор $\mathbf {r} _{i}$ не вращался бы, если бы ось вращения была параллельна ей, и, следовательно, он описывал бы только вращение вокруг оси, перпендикулярной ей (т. е. он не видел бы параллельную ему составляющую псевдовектора угловой скорости и позволял бы только вычислить компонента, перпендикулярного ему). Положение частицы теперь записывается как:

$\mathbf {R} _{i}=\mathbf {R} +{\mathcal {R}}\mathbf {r} _{io}$

Взяв производную по времени, получим скорость частицы:

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}\mathbf {r} _{io}$

где V _i — скорость частицы (в лабораторной системе координат), а V — скорость O ′ (начало координат твердого тела). С ${\mathcal {R}}$ — матрица вращения, обратная ей — транспонированная. Итак, мы заменяем ${\mathcal {I}}={\mathcal {R}}^{\text{T}}{\mathcal {R}}$:

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}{\mathcal {I}}\mathbf {r} _{io}$

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}{\mathcal {R}}^{\text{T}}{\mathcal {R}}\mathbf {r} _{io}$

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}{\mathcal {R}}^{\text{T}}\mathbf {r} _{i}$

или

$\mathbf {V} _{i}=\mathbf {V} +\Omega \mathbf {r} _{i}$

где $\Omega ={\frac {d{\mathcal {R}}}{dt}}{\mathcal {R}}^{\text{T}}$ — предыдущий тензор угловой скорости.

Можно доказать , что это кососимметричная матрица , поэтому мы можем взять ее двойственный вектор , чтобы получить трехмерный псевдовектор, который в точности соответствует предыдущему вектору угловой скорости. ${\boldsymbol {\omega }}$:

${\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]$

Подставив ω вместо Ω в приведенное выше выражение скорости и заменив умножение матрицы эквивалентным векторным произведением:

$\mathbf {V} _{i}=\mathbf {V} +{\boldsymbol {\omega }}\times \mathbf {r} _{i}$

Видно, что скорость точки в твердом теле можно разделить на два слагаемых: скорость опорной точки, закрепленной в твердом теле, плюс член векторного произведения, включающий орбитальную угловую скорость частицы относительно эталона. точка. Эта угловая скорость — это то, что физики называют «угловой скоростью вращения» твердого тела, в отличие от орбитальной угловой скорости опорной точки O ′ относительно начала координат O .

Последовательность

Мы предположили, что твердое тело вращается вокруг произвольной точки. Мы должны доказать, что ранее определенная угловая скорость вращения не зависит от выбора начала координат, а это означает, что угловая скорость вращения является внутренним свойством вращающегося твердого тела. (Обратите внимание на заметный контраст с орбитальной угловой скоростью точечной частицы, которая, безусловно, зависит от выбора источника.)

Доказательство независимости угловой скорости вращения от выбора начала координат.

См. график справа: начало координат лабораторной системы координат — O , а O ₁ и O ₂ — две неподвижные точки твердого тела, скорость которых равна $\mathbf {v} _{1}$ и $\mathbf {v} _{2}$ соответственно. Предположим, что угловая скорость относительно O ₁ и O ₂ равна ${\boldsymbol {\omega }}_{1}$ и ${\boldsymbol {\omega }}_{2}$ соответственно. Поскольку точки Р и О ₂ имеют только одну скорость,

$\mathbf {v} _{1}+{\boldsymbol {\omega }}_{1}\times \mathbf {r} _{1}=\mathbf {v} _{2}+{\boldsymbol {\omega }}_{2}\times \mathbf {r} _{2}$

$\mathbf {v} _{2}=\mathbf {v} _{1}+{\boldsymbol {\omega }}_{1}\times \mathbf {r} =\mathbf {v} _{1}+{\boldsymbol {\omega }}_{1}\times (\mathbf {r} _{1}-\mathbf {r} _{2})$

Из двух вышесказанных следует, что

$({\boldsymbol {\omega }}_{2}-{\boldsymbol {\omega }}_{1})\times \mathbf {r} _{2}=0$

Поскольку точка P (и, следовательно, $\mathbf {r} _{2}$) произвольно, то отсюда следует, что

${\boldsymbol {\omega }}_{1}={\boldsymbol {\omega }}_{2}$

Если опорной точкой является мгновенная ось вращения, выражение скорости точки твердого тела будет иметь только член угловой скорости. Это происходит потому, что скорость мгновенной оси вращения равна нулю. Примером мгновенной оси вращения является дверная петля. Другой пример — точка контакта чисто катящегося сферического (или, в более общем смысле, выпуклого) твердого тела.