Теорема Эйлера о вращении

В геометрии утверждает , теорема Эйлера о вращении что в трехмерном пространстве любое смещение твердого тела , при котором точка твердого тела остается неподвижной, эквивалентно одному повороту вокруг некоторой оси, проходящей через фиксированную точку . Это также означает, что композиция двух ротаций также является ротацией. Поэтому набор вращений имеет групповую структуру, известную как группа вращений .

Теорема названа в честь Леонарда Эйлера , который доказал ее в 1775 году с помощью сферической геометрии . Ось вращения известна как ось Эйлера и обычно представлена единичным вектором $ê$ . Его произведение на угол поворота известно как вектор оси-угла . Распространение теоремы на кинематику дает понятие мгновенной оси вращения , линии неподвижных точек.

В терминах линейной алгебры теорема утверждает, что в трехмерном пространстве любые две декартовы системы координат с общим началом связаны вращением вокруг некоторой фиксированной оси. Это также означает, что произведение двух матриц вращения снова является матрицей вращения и что для нетождественной матрицы вращения одно собственное значение равно 1, а два других являются комплексными или оба равны -1. соответствующий Собственный вектор, этому собственному значению, является осью вращения, соединяющей две системы.

Теорема Эйлера (1776 г.)

Эйлер формулирует теорему следующим образом: ^{[ 1 ]}

Теорема. Как бы сфера ни вращалась вокруг своего центра, ей всегда можно присвоить диаметр , направление которого в транслируемом положении совпадает с исходным положением.

или (на английском языке):

При перемещении сферы вокруг своего центра всегда можно найти диаметр, направление которого в смещенном положении такое же, как и в исходном.

Доказательство

Первоначальное доказательство Эйлера было проведено с использованием сферической геометрии , и поэтому всякий раз, когда он говорит о треугольниках, их следует понимать как сферические треугольники .

Предыдущий анализ

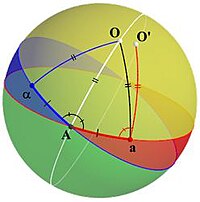
Чтобы прийти к доказательству, Эйлер анализирует, как бы выглядела ситуация, если бы теорема была верна. Для этого предположим, что желтая линия на рисунке 1 проходит через центр сферы и является искомой осью вращения, а точка $O$ является одной из двух точек пересечения этой оси со сферой. Затем он рассматривает произвольный большой круг, не содержащий $O$ (синий круг), и его изображение после вращения (красный круг), которое является еще одним большим кругом, не $O.$ содержащим Он называет точку их пересечения $А.$ точкой (Если окружности совпадают, то за $А$ можно взять любую точку на любой из них; в противном случае $А$ — одна из двух точек пересечения.)

Теперь $А$ находится на исходном круге (синий круг), поэтому его изображение будет на транспортируемом круге (красный). Он называет это изображение точкой $а$ . Поскольку $точка A$ также находится на транспортируемом круге (красный), это изображение другой точки, которая была на исходном круге (синий), и он помечает это прообраз как $α$ (см. рисунок 2 ). Затем он рассматривает две дуги, $α$ и $a$ с $A.$ соединяющие Эти дуги имеют одинаковую длину, поскольку дуга $αA$ отображается в дугу $Aa$ . Кроме того, поскольку $O$ является фиксированной точкой, треугольник $αOA$ отображается в треугольник $AOa$ , поэтому эти треугольники являются равнобедренными, а дуга $AO$ делит угол пополам $∠ αAa$ .

Строительство точки лучшего кандидата

Построим точку, которая могла бы быть инвариантной, используя предыдущие соображения. Начнем с большого синего круга и его изображения после преобразования, которое представляет собой большой красный круг, как на рисунке 1 . Пусть точка $А$ будет точкой пересечения этих окружностей. Если $изображение А$ при преобразовании является той же самой точкой, то $А$ является неподвижной точкой преобразования, а поскольку центр также является фиксированной точкой, диаметр сферы, содержащей $А,$ является осью вращения, и теорема доказана.

В противном случае мы помечаем $a$ образ A как $,$ а его прообраз как $α$ и соединяем эти две точки с $A$ дугами $αA$ и $Aa$ . Эти дуги имеют одинаковую длину. Постройте большой круг, который делит пополам $∠ αAa$ , и расположите точку $O$ на этом большом круге так, чтобы дуги $AO$ и $aO$ имели одинаковую длину, и назовите область сферы, содержащую $O$ и ограниченную синим и красным большими кругами, внутренней частью $∠ αAa.$ . (То есть желтая область на рисунке 3. ) Тогда, поскольку $αA = Aa$ и $O$ находится на биссектрисе $∠ αAa$ , мы также имеем $αO = aO$ .

Доказательство его инвариантности относительно преобразования.

Теперь предположим, что $’$ — это образ $O.$ O Тогда мы знаем, $что ∠ αAO = ∠ AaO'$ и ориентация сохраняется, ^{[ а ]} поэтому $O'$ должен быть внутренним по отношению к $∠ αAa$ . Теперь $AO$ преобразуется в $aO'$ , поэтому $AO = aO'$ . Поскольку $длина AO$ также равна длине $aO$ , то $aO = aO'$ и $∠ AaO = ∠ aAO$ . Но $∠ αAO = ∠ aAO$ , поэтому $∠ αAO = ∠ AaO$ и $∠ AaO = ∠ AaO'$ . Следовательно, $'$ — это та же точка, что и $O.$ O Другими словами, $O$ — это фиксированная точка преобразования, а поскольку центр также является фиксированной точкой, диаметр сферы, содержащей $O,$ является осью вращения.

Заключительные замечания о строительстве

Оригинальный рисунок Эйлера, где ABC — синий круг, а ACc — красный круг.

Эйлер также указывает, что $O$ можно найти, пересекая биссектрису $Aa$ с биссектрисой $∠ αAa$ , что на практике может оказаться проще. Он также предложил пересечение двух плоскостей:

плоскость симметрии угла $∠ αAa$ (проходящая через центр $C$ сферы) и
плоскость симметрии дуги $Аа$ (которая также проходит через $С$ ).

Предложение . Эти две плоскости пересекаются по диаметру. Именно этот диаметр нам и нужен.

Доказательство . Назовем

О

любой из концов (их два) этого диаметра над поверхностью сферы. Так как

αA

отображается на

Aa

и треугольники имеют одинаковые углы, то треугольник

OαA

переносится на треугольник

OAa

. Поэтому точка

О

должна оставаться неподвижной при движении.

Следствия . Это также показывает, что вращение сферы можно рассматривать как два последовательных отражения относительно двух описанных выше плоскостей. Точки в зеркальной плоскости инвариантны относительно отражения, и, следовательно, точки на их пересечении (линия: ось вращения) инвариантны как относительно отражений, так и, следовательно, относительно вращения.

Другой простой способ найти ось вращения — рассмотреть плоскость, на которой $α$ , $A$ ,. $точки$ лежат Ось вращения, очевидно, ортогональна этой плоскости и проходит через центр $С$ сферы.

Учитывая, что для твердого тела любое движение, которое оставляет ось инвариантной, является вращением, это также доказывает, что любая произвольная композиция вращений эквивалентна одному вращению вокруг новой оси.

Матричное доказательство

Пространственное вращение — это линейная карта во взаимно однозначном соответствии с 3 × 3 матрицей вращения $R$ , которая преобразует координатный вектор $x$ в $X$ то есть $Rx = X.$ , Следовательно, другая версия теоремы Эйлера состоит в том, что для каждого поворота $R$ существует ненулевой вектор $n$ , для которого $Rn = n$ ; это в точности утверждение, что $n$ является собственным вектором R $,$ связанным с собственным значением 1. Следовательно, достаточно доказать, что 1 является собственным значением $R$ ; осью вращения $R$ будет линия $µ n$ , где $n$ — собственный вектор с собственным значением 1.

Матрица вращения обладает тем фундаментальным свойством, что ее инверсия является ее транспонированием, то есть

\mathbf {R} ^{\mathsf {T}}\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathsf {T}}=\mathbf {I} ,

где $I$ — единичная матрица 3 × 3 , а верхний индекс T указывает на транспонированную матрицу.

Вычислив определитель этого отношения, вы обнаружите, что матрица вращения имеет определитель ±1. В частности,

{\begin{aligned}1=\det(\mathbf {I} )&=\det \left(\mathbf {R} ^{\mathsf {T}}\mathbf {R} \right)=\det \left(\mathbf {R} ^{\mathsf {T}}\right)\det(\mathbf {R} )=\det(\mathbf {R} )^{2}\\\Longrightarrow \qquad \det(\mathbf {R} )&=\pm 1.\end{aligned}}

Матрица поворота с определителем +1 представляет собой правильный поворот, а матрица с отрицательным определителем -1 представляет собой неправильный поворот , то есть отражение в сочетании с правильным поворотом.

Теперь будет показано, что матрица собственного вращения $R$ имеет по крайней мере один инвариантный вектор $n$ , т. е. $Rn = n$ . Поскольку для этого требуется, чтобы $(R - I) n = 0$ , мы видим, что вектор $n$ должен быть собственным вектором матрицы $R$ с собственным значением $λ = 1$ . Таким образом, это эквивалентно показу, что $det(R - I) = 0$ .

Используйте два отношения

\det(-\mathbf {A} )=(-1)^{3}\det(\mathbf {A} )=-\det(\mathbf {A} )\quad

для любой 3 × 3 матрицы A и

\det \left(\mathbf {R} ^{-1}\right)=1\quad

(поскольку $det(R) = 1$ ) для вычисления

{\begin{aligned}&\det(\mathbf {R} -\mathbf {I} )=\det \left((\mathbf {R} -\mathbf {I} )^{\mathsf {T}}\right)\\{}={}&\det \left(\mathbf {R} ^{\mathsf {T}}-\mathbf {I} \right)=\det \left(\mathbf {R} ^{-1}-\mathbf {R} ^{-1}\mathbf {R} \right)\\{}={}&\det \left(\mathbf {R} ^{-1}(\mathbf {I} -\mathbf {R} )\right)=\det \left(\mathbf {R} ^{-1}\right)\,\det(-(\mathbf {R} -\mathbf {I} ))\\{}={}&-\det(\mathbf {R} -\mathbf {I} )\\[3pt]\Longrightarrow \ 0={}&\det(\mathbf {R} -\mathbf {I} ).\end{aligned}}

Это показывает, что $λ = 1$ является корнем (решением) характеристического уравнения , т. е.

\det(\mathbf {R} -\lambda \mathbf {I} )=0\quad {\hbox{for}}\quad \lambda =1.

Другими словами, матрица $R - I$ сингулярна и имеет ненулевое ядро , то есть существует хотя бы один ненулевой вектор, скажем $n$ , для которого

(\mathbf {R} -\mathbf {I} )\mathbf {n} =\mathbf {0} \quad \Longleftrightarrow \quad \mathbf {R} \mathbf {n} =\mathbf {n} .

Линия $µ n$ для вещественного $µ$ инвариантна относительно $R$ , т. е. $µ n$ является осью вращения. Это доказывает теорему Эйлера.

Эквивалентность ортогональной матрицы матрице вращения

Две матрицы (представляющие линейные карты) называются эквивалентными, если при изменении базиса одна становится равной другой. Правильная ортогональная матрица всегда эквивалентна (в этом смысле) либо следующей матрице, либо ее вертикальному отражению:

\mathbf {R} \sim {\begin{pmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\\\end{pmatrix}},\qquad 0\leq \phi \leq 2\pi .

Тогда любая ортогональная матрица является либо вращением, либо неправильным вращением . Общая ортогональная матрица имеет только одно действительное собственное значение: +1 или -1. Когда это +1, матрица является поворотом. Когда −1, матрица представляет собой неправильный поворот.

Если $R$ имеет более одного инвариантного вектора, то $= 0$ и $R = I.$ φ Любой вектор является инвариантным вектором $I$ .

Экскурс в теорию матриц

Для доказательства предыдущего уравнения необходимо вспомнить некоторые факты из теории матриц.

размера $m \times m$ Матрица $A$ имеет $m$ ортогональных собственных векторов тогда и только тогда, когда $,$ то A нормальна есть если $A † А = АА †$ . ^{[ б ]} Этот результат эквивалентен утверждению, что нормальные матрицы можно привести к диагональной форме с помощью унитарного преобразования подобия:

\mathbf {A} \mathbf {U} =\mathbf {U} \;\operatorname {diag} (\alpha _{1},\ldots ,\alpha _{m})\quad \Longleftrightarrow \quad \mathbf {U} ^{\dagger }\mathbf {A} \mathbf {U} =\operatorname {diag} (\alpha _{1},\ldots ,\alpha _{m}),

и $U$ унитарно, т. е.

\mathbf {U} ^{\dagger }=\mathbf {U} ^{-1}.

Собственные значения $α 1, ..., α m$ являются корнями характеристического уравнения. Если матрица $A$ унитарна (заметим, что унитарные матрицы нормальны), то

\left(\mathbf {U} ^{\dagger }\mathbf {A} \mathbf {U} \right)^{\dagger }=\operatorname {diag} \left(\alpha _{1}^{*},\ldots ,\alpha _{m}^{*}\right)=\mathbf {U} ^{\dagger }\mathbf {A} ^{-1}\mathbf {U} =\operatorname {diag} \left({\frac {1}{\alpha _{1}}},\ldots ,{\frac {1}{\alpha _{m}}}\right)

откуда следует, что собственные значения унитарной матрицы лежат на единичной окружности комплексной плоскости:

\alpha _{k}^{*}={\frac {1}{\alpha _{k}}}\quad \Longleftrightarrow \quad \alpha _{k}^{*}\alpha _{k}=\left|\alpha _{k}\right|^{2}=1,\qquad k=1,\ldots ,m.

Также ортогональная (действительная унитарная) матрица имеет собственные значения на единичной окружности в комплексной плоскости. Более того, поскольку его характеристическое уравнение ( $многочлен m$ -го порядка от $λ$ ) имеет вещественные коэффициенты, отсюда следует, что его корни появляются в комплексно-сопряженных парах, то есть, если $α$ является корнем, то и $α является корнем. *$ . Корней 3, поэтому хотя бы один из них должен быть чисто вещественным (+1 или −1).

Вспомнив эти общие факты из теории матриц, вернемся к матрице $R.$ вращения Из его реальности и ортогональности следует, что мы можем найти $U$ такое, что:

\mathbf {R} \mathbf {U} =\mathbf {U} {\begin{pmatrix}e^{i\phi }&0&0\\0&e^{-i\phi }&0\\0&0&\pm 1\\\end{pmatrix}}

Если можно найти матрицу $U$ , которая дает указанную выше форму, и существует только один чисто вещественный компонент, равный −1, то мы определяем $\mathbf {R}$ быть неправильным вращением. Давайте тогда рассмотрим только случай матриц R, которые являются собственными вращениями (третье собственное значение равно 1). Тогда третий столбец 3 × 3 матрицы $U$ будет равен инвариантному вектору $n$ . Записав $u 1$ и $u 2$ для первых двух столбцов $U$ , это уравнение дает

\mathbf {R} \mathbf {u} _{1}=e^{i\phi }\,\mathbf {u} _{1}\quad {\hbox{and}}\quad \mathbf {R} \mathbf {u} _{2}=e^{-i\phi }\,\mathbf {u} _{2}.

Если $u 1$ имеет собственное значение 1, то $φ = 0$ и $u 2$ также имеет собственное значение 1, из чего следует, что в этом случае $R = I$ . Однако в целом, как $(\mathbf {R} -e^{i\phi }\mathbf {I} )\mathbf {u} _{1}=0$ подразумевает, что также $(\mathbf {R} -e^{-i\phi }\mathbf {I} )\mathbf {u} _{1}^{*}=0$ держится, так что $\mathbf {u} _{2}=\mathbf {u} _{1}^{*}$ можно выбрать для $\mathbf {u} _{2}$ . Сходным образом, $(\mathbf {R} -\mathbf {I} )\mathbf {u} _{3}=0$ может привести к $\mathbf {u} _{3}$ только с реальными записями, для правильной матрицы вращения $\mathbf {R}$ . Наконец, матричное уравнение преобразуется с помощью унитарной матрицы:

\mathbf {R} \mathbf {U} {\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\{\frac {1}{\sqrt {2}}}&{\frac {-i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}=\mathbf {U} \underbrace {{\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\{\frac {1}{\sqrt {2}}}&{\frac {-i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&0\\{\frac {-i}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}} _{=\;\mathbf {I} }{\begin{pmatrix}e^{i\phi }&0&0\\0&e^{-i\phi }&0\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\{\frac {1}{\sqrt {2}}}&{\frac {-i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}

что дает

\mathbf {U'} ^{\dagger }\mathbf {R} \mathbf {U'} ={\begin{pmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\\\end{pmatrix}}\quad {\text{ with }}\quad \mathbf {U'} =\mathbf {U} {\begin{pmatrix}{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt {2}}}&0\\{\frac {1}{\sqrt {2}}}&{\frac {-i}{\sqrt {2}}}&0\\0&0&1\\\end{pmatrix}}.

Столбцы $U'$ ортонормированы, поскольку это унитарная матрица только с вещественными элементами, согласно ее определению, приведенному выше, что $\mathbf {u} _{1}$ представляет собой комплексное сопряжение $\mathbf {u} _{2}$ и это $\mathbf {u} _{3}$ представляет собой вектор с вещественными компонентами. Третий столбец по-прежнему $\mathbf {u} _{3}=$ $n$ , два других столбца $U'$ перпендикулярны $n$ . Теперь мы можем увидеть, как наше определение неправильного вращения соответствует геометрической интерпретации: неправильное вращение — это вращение вокруг оси (здесь оси, соответствующей третьей координате) и отражение в плоскости, перпендикулярной этой оси. Если мы ограничимся только матрицами с определителем 1, мы увидим, что они должны быть собственными вращениями. Из этого результата следует, что любая ортогональная матрица $R,$ соответствующая собственному повороту, эквивалентна повороту на угол $φ$ вокруг оси $n$ .

Классы эквивалентности

След 1 (сумма диагональных элементов) реальной матрицы вращения, приведенной выше, равен $+ 2 cos φ$ . Поскольку след инвариантен относительно преобразования подобия ортогональной матрицы,

\mathrm {Tr} \left[\mathbf {A} \mathbf {R} \mathbf {A} ^{\mathsf {T}}\right]=\mathrm {Tr} \left[\mathbf {R} \mathbf {A} ^{\mathsf {T}}\mathbf {A} \right]=\mathrm {Tr} [\mathbf {R} ]\quad {\text{ with }}\quad \mathbf {A} ^{\mathsf {T}}=\mathbf {A} ^{-1},

отсюда следует, что все матрицы, эквивалентные $R$ посредством таких ортогональных матричных преобразований, имеют один и тот же след: след является функцией класса . Это матричное преобразование, очевидно, является отношением эквивалентности , то есть все такие эквивалентные матрицы образуют класс эквивалентности.

Фактически, все вращения 3 × 3 матрицы собственного вращения образуют группу , обычно обозначаемую SO (3) (специальная ортогональная группа в 3 измерениях), и все матрицы с одним и тем же следом образуют класс эквивалентности в этой группе. Все элементы такого класса эквивалентности имеют общий угол поворота , но все повороты происходят вокруг разных осей. Если $n$ — собственный вектор $R$ с собственным значением 1, то $An$ также является собственным вектором $ARA.$ ^Т, также с собственным значением 1. Если $A = I$ , $n$ и $An$ не различны.

Приложения

Генераторы вращений

Предположим, мы задаем ось вращения единичным вектором $[x, y, z]$ и предположим, что у нас есть бесконечно малое вращение на угол $Δ θ$ вокруг этого вектора. Если разложить матрицу вращения как бесконечное сложение и использовать подход первого порядка, матрица вращения $Δ R$ будет представлена как:

\Delta R={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}+{\begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0\end{bmatrix}}\,\Delta \theta =\mathbf {I} +\mathbf {A} \,\Delta \theta .

Конечное вращение на угол $θ$ вокруг этой оси можно рассматривать как последовательность небольших вращений вокруг одной и той же оси. Аппроксимируя $Δ θ$ как $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ θ / N ⁠$ где $N$ — большое число, вращение $θ$ вокруг оси можно представить как:

R=\left(\mathbf {1} +{\frac {\mathbf {A} \theta }{N}}\right)^{N}\approx e^{\mathbf {A} \theta }.

Можно видеть, что теорема Эйлера по существу утверждает, что все вращения могут быть представлены в этой форме. Продукт $A θ$ является «генератором» конкретного вращения, являясь вектором $(x, y, z),$ связанным с матрицей $A$ . Это показывает, что матрица вращения и формат ось-угол связаны экспоненциальной функцией.

Можно вывести простое выражение для $G.$ генератора Начинаем с произвольной плоскости (в евклидовом пространстве), определяемой парой перпендикулярных единичных векторов $a$ и $b$ . В этой плоскости можно выбрать произвольный вектор $x$ с перпендикуляром $y$ . Затем вычисляется значение $y$ через $x$ , и подстановка в выражение для вращения в плоскости дает матрицу вращения $R$ , которая включает генератор $G = ba.$ ^Т $- аб$ ^Т.

{\begin{aligned}\mathbf {x} &=\mathbf {a} \cos \alpha +\mathbf {b} \sin \alpha \\\mathbf {y} &=-\mathbf {a} \sin \alpha +\mathbf {b} \cos \alpha \\[8pt]\cos \alpha &=\mathbf {a} ^{\mathsf {T}}\mathbf {x} \\\sin \alpha &=\mathbf {b} ^{\mathsf {T}}\mathbf {x} \\[8px]\mathbf {y} &=-\mathbf {ab} ^{\mathsf {T}}\mathbf {x} +\mathbf {ba} ^{\mathsf {T}}\mathbf {x} =\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\mathbf {x} \\[8px]\mathbf {x} '&=\mathbf {x} \cos \beta +\mathbf {y} \sin \beta \\&=\left(\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \right)\mathbf {x} \\[8px]\mathbf {R} &=\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \\&=\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \\[8px]\mathbf {G} &=\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\end{aligned}}

Чтобы включить в вращение векторы вне плоскости, необходимо изменить приведенное выше выражение для $R$ , включив в него два оператора проекции , которые разделяют пространство. Эту модифицированную матрицу вращения можно переписать как экспоненциальную функцию .

{\begin{aligned}\mathbf {P_{ab}} &=-\mathbf {G} ^{2}\\\mathbf {R} &=\mathbf {I} -\mathbf {P_{ab}} +\left(\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \right)\mathbf {P_{ab}} =e^{\mathbf {G} \beta }\end{aligned}}

Анализ часто проще с точки зрения этих генераторов, а не полной матрицы вращения. Анализ в терминах генераторов известен как алгебра Ли группы вращений.

Кватернионы

Из теоремы Эйлера следует, что относительная ориентация любой пары систем координат может быть задана набором из трех независимых чисел. Иногда для упрощения операций с алгеброй кватернионов добавляется избыточное четвертое число. Три из этих чисел представляют собой направляющие косинусы, ориентирующие собственный вектор. Четвертый — это угол вокруг собственного вектора, разделяющий два набора координат. Такой набор из четырех чисел называется кватернионом .

Хотя описанный выше кватернион не включает в себя комплексные числа , если кватернионы используются для описания двух последовательных вращений, их необходимо объединить с помощью некоммутативной алгебры кватернионов, полученной Уильямом Роуэном Гамильтоном с использованием мнимых чисел.

Расчет вращения с помощью кватернионов пришел на смену использованию направляющих косинусов в аэрокосмических приложениях благодаря сокращению необходимых вычислений и способности минимизировать ошибки округления . Кроме того, в компьютерной графике имеет значение возможность сравнительно легко выполнять сферическую интерполяцию между кватернионами.

Обобщения

В более высоких измерениях любое твердое движение, сохраняющее точку в размерности $2 n$ или $2 n + 1,$ представляет собой композицию не более $n$ вращений в ортогональных плоскостях вращения , хотя эти плоскости не обязательно должны быть определены однозначно, и жесткое движение может фиксировать несколько топоры. Кроме того, любое твердое движение, сохраняющее $n$ линейно независимых точек, охватывающее $n$ -мерное тело в размерности $2 n$ или $2 n + 1$ , представляет собой единую плоскость вращения . Другими словами, если два твердых тела с одинаковой геометрией имеют внутри себя как минимум $n$ точек «идентичных» положений, выпуклая оболочка которых является $n$ -мерной, то одно плоское вращение может привести к тому, что одно из них покроет другое. точно в размерности $2 n$ или $2 n + 1$ .

Жесткое движение в трех измерениях, которое не обязательно фиксирует точку, называется «винтовым движением». Это связано с тем, что композиция вращения с перемещением, перпендикулярным оси, представляет собой вращение вокруг параллельной оси, а композиция с перемещением, параллельным оси, дает винтовое движение; см . ось винта . Это порождает теорию винта .

См. также

углы Эйлера
Формула Эйлера – Родригеса
Формализмы вращения в трех измерениях
Угловая скорость
Вращение вокруг фиксированной оси
Матричная экспонента
Представление оси-угла
Теорема Часла (кинематика) для расширения, касающегося общих перемещений твердого тела.

Примечания

^ Ориентация сохраняется в том смысле, что если $αA$ поворачивается вокруг $A$ против часовой стрелки, чтобы совместить с $OA$ , то $Aa$ необходимо повернуть вокруг против $часовой$ стрелки, чтобы совместить с $O'a$ . Аналогично, если вращение происходит по часовой стрелке.
^ Символ кинжала $†$ обозначает комплексное сопряжение с последующей транспозицией. Для реальных матриц комплексное сопряжение ничего не дает, и перечеркнуть реальную матрицу - это то же самое, что ее транспонировать.

Ссылки

^ Новые комментарии Петрополитической академии наук 20, 1776, стр. 189–207 (Е478)

Эта статья включает в себя материал из статьи Citizendium « Теорема Эйлера (вращение) », которая распространяется под лицензией Creative Commons Attribution-ShareAlike 3.0 Unported License , но не под GFDL .

Теорема Эйлера и ее доказательство содержатся в параграфах 24–26 приложения ( Additamentum . стр. 201–203) Л. Эйлера (Leonhard Euler) « Общие формулы перевода произвольных твердых тел», представленного в Санкт-Петербургском университете. Петербургской академии 9 октября 1775 года и впервые опубликовано в «Новых записках Петрополитической академии наук» 20 , 1776, с. 189–207 (E478) и был переиздан в «Теории движения твердых тел» под ред. новый, 1790, с. 449–460 (E478a) и позже в собрании сочинений Opera Omnia , Series 2, Volume 9 , pp. 84–98.
Пале, Боб; Пале, Ришар; Роди, Стивен (2009). «Дезориентирующий взгляд на теорему Эйлера об оси вращения». Американский математический ежемесячник . 116 (10): 892–909. дои : 10.4169/000298909x477014 .

Внешние ссылки

Оригинальный трактат Эйлера в Архиве Эйлера : запись на E478 , первая публикация 1776 г. ( pdf )
Оригинальный текст Эйлера (на латыни) и английский перевод (Йохан Стен)
Демонстрационный проект Вольфрама по теореме Эйлера о вращении (Том Верхуфф)

[2] Ориентация сохраняется в том смысле, что если $αA$ поворачивается вокруг $A$ против часовой стрелки, чтобы совместить с $OA$ , то $Aa$ необходимо повернуть вокруг против $часовой$ стрелки, чтобы совместить с $O'a$ . Аналогично, если вращение происходит по часовой стрелке.

[3] Символ кинжала $†$ обозначает комплексное сопряжение с последующей транспозицией. Для реальных матриц комплексное сопряжение ничего не дает, и перечеркнуть реальную матрицу - это то же самое, что ее транспонировать.

[1] Новые комментарии Петрополитической академии наук 20, 1776, стр. 189–207 (Е478)

[ 1 ]

[ а ]

[ б ]