Уравнения Эйлера (гидродинамика)

Эта статья посвящена уравнениям Эйлера в потоке классической жидкости. Чтобы узнать о других значениях, см. Список тем, названных в честь Леонарда Эйлера .

На этой странице предполагается, что классическая механика применяется ; Для обсуждения потока сжимаемой жидкости, когда скорости приближаются к скорости света, см. релятивистские уравнения Эйлера .

Обтекание крыла. Этот несжимаемый поток удовлетворяет уравнениям Эйлера.

В гидродинамике представляют уравнения Эйлера собой набор дифференциальных уравнений в частных производных, управляющих адиабатическим и невязким потоком . Они названы в честь Леонарда Эйлера . В частности, им соответствуют уравнения Навье–Стокса с нулевой вязкостью и нулевой теплопроводностью .

Уравнения Эйлера применимы к несжимаемым и сжимаемым потокам . Уравнения Эйлера для несжимаемой жидкости состоят из уравнений Коши для сохранения массы и баланса импульса, а также из условия несжимаемости, согласно которому скорость потока представляет собой соленоидальное поле . Уравнения Эйлера для сжимаемой жидкости состоят из уравнений сохранения массы, баланса импульса и баланса энергии, а также подходящего определяющего уравнения для удельной плотности энергии жидкости. Исторически Эйлер вывел только уравнения сохранения массы и баланса импульса. Однако в литературе по гидродинамике полный набор уравнений Эйлера для сжимаемости, включая уравнение энергии, часто называется «уравнениями Эйлера для сжимаемости».

Математический характер уравнений Эйлера для несжимаемой и сжимаемой систем весьма различен. Для постоянной плотности жидкости уравнения несжимаемой жидкости можно записать как квазилинейное уравнение переноса для скорости жидкости вместе с эллиптическим уравнением Пуассона для давления. С другой стороны, сжимаемые уравнения Эйлера образуют квазилинейную гиперболическую систему уравнений сохранения .

Уравнения Эйлера могут быть сформулированы в «конвективной форме» (также называемой « лагранжевой формой ») или в «форме сохранения» (также называемой « эйлеровой формой »). Конвективная форма подчеркивает изменения состояния в системе отсчета, движущейся вместе с жидкостью. Форма сохранения подчеркивает математическую интерпретацию уравнений как уравнений сохранения контрольного объема, фиксированного в пространстве (что полезнос числовой точки зрения).

История

Уравнения Эйлера впервые появились в опубликованной форме в статье Эйлера «Общие принципы движения жидкостей», опубликованной в « Mémoires de l'Académie des Sciences de Berlin» в 1757 году. (хотя Эйлер ранее представил свою работу Берлинской академии в 1752 году). Уравнения Эйлера были одними из первых уравнений в частных производных записанных после волнового уравнения . В оригинальной работе Эйлера система уравнений состояла из уравнений импульса и неразрывности и поэтому была недоопределенной, за исключением случая несжимаемого потока. Дополнительное уравнение, получившее название адиабатического условия , было предложено Пьером-Симоном Лапласом в 1816 году.

Во второй половине XIX века было обнаружено, что уравнение, связанное с балансом энергии, должно всегда соблюдаться для сжимаемых течений, а условие адиабаты является следствием основных законов в случае гладких решений. С открытием специальной теории относительности понятия плотности энергии, плотности импульса и напряжения были объединены в понятие тензора энергии-импульса , а энергия и импульс также были объединены в единое понятие вектора энергии-импульса. .

жидкости с постоянной и однородной

В конвективной форме (т. е. форме с оператором конвекции , явным в уравнении количества движения ) уравнения Эйлера для несжимаемой жидкости в случае постоянной плотности во времени и однородности в пространстве имеют вид:

Уравнения Эйлера несжимаемой жидкости с постоянной и однородной плотностью
( конвективная или лагранжева форма )

$\left\{{\begin{aligned}{D\mathbf {u} \over Dt}&=-\nabla w+\mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.$

где:

• $\mathbf {u}$ вектор скорости потока N с компонентами в -мерном пространстве $u_{1},u_{2},\dots ,u_{N}$,
• ${\frac {D{\boldsymbol {\Phi }}}{Dt}}={\frac {\partial {\boldsymbol {\Phi }}}{\partial t}}+\mathbf {v} \cdot \nabla {\boldsymbol {\Phi }}$, для общей функции (или поля) ${\boldsymbol {\Phi }}$ обозначает его материальную производную во времени относительно адвективного поля $\mathbf {v}$ и
• $\nabla w$ — градиент удельной (в смысле единицы массы ) термодинамической работы , внутренний исходный член и
• $\nabla \cdot \mathbf {u}$ скорости потока – дивергенция .
• $\mathbf {g}$ представляет ускорения тела (на единицу массы), действующие на континуум, например гравитацию , инерционные ускорения , ускорение электрического поля и т. д.

Первое уравнение представляет собой уравнение количества движения Эйлера с однородной плотностью (для этого уравнения оно также не может быть постоянным во времени). Расширяя материальную производную , уравнения принимают вид:

$$\left\{{\begin{aligned}{\partial \mathbf {u} \over \partial t}+(\mathbf {u} \cdot \nabla )\mathbf {u} &=-\nabla w+\mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.$$

Фактически для потока с однородной плотностью $\rho _{0}$ имеет место следующее тождество:

$$\nabla w\equiv \nabla \left({\frac {p}{\rho _{0}}}\right)={\frac {1}{\rho _{0}}}\nabla p$$

где $p$ это механическое давление . Второе уравнение представляет собой несжимаемую связь , утверждая, что скорость потока представляет собой соленоидальное поле (порядок уравнений не является причинным, но подчеркивает тот факт, что несжимаемая связь не является вырожденной формой уравнения неразрывности , а скорее уравнения энергии , как станет ясно из дальнейшего). Примечательно, что уравнение неразрывности потребуется и в этом несжимаемом случае в качестве дополнительного третьего уравнения в случае изменения плотности во времени или в пространстве. Например, при однородной, но изменяющейся во времени плотности уравнение неразрывности, добавляемое к приведенному выше набору, будет соответствовать:

$${\frac {\partial \rho }{\partial t}}=0$$

Таким образом, случай постоянной и однородной плотности является единственным, который не требует уравнения неразрывности в качестве дополнительного уравнения независимо от наличия или отсутствия несжимаемой связи. Фактически, случай несжимаемых уравнений Эйлера с постоянной и однородной плотностью, обсуждаемый здесь, представляет собой игрушечную модель , включающую только два упрощенных уравнения, поэтому он идеален для дидактических целей, даже если и имеет ограниченную физическую значимость.

Таким образом, приведенные выше уравнения представляют соответственно сохранение массы (1 скалярное уравнение) и импульса (1 векторное уравнение, содержащее $N$ скалярные компоненты, где $N$ — физическое измерение интересующего пространства). Скорость потока и давление являются так называемыми физическими переменными .

В системе координат, заданной $\left(x_{1},\dots ,x_{N}\right)$ векторы скорости и внешней силы $\mathbf {u}$ и $\mathbf {g}$ иметь компоненты $(u_{1},\dots ,u_{N})$ и $\left(g_{1},\dots ,g_{N}\right)$, соответственно. Тогда уравнения можно выразить в индексной записи следующим образом:

Особенности $\left\{{\begin{aligned}{\partial u_{i} \over \partial t}+\sum _{j=1}^{N}{\partial \left(u_{i}u_{j}+w\delta _{ij}\right) \over \partial x_{j}}&=g_{i}\\\sum _{i=1}^{N}{\partial u_{i} \over \partial x_{i}}&=0\end{aligned}}\right.$

где $i$ и $j$ нижние индексы обозначают компоненты N -мерного пространства, а $\delta _{ij}$ – это дельта Кренекера . используется нотация Эйнштейна (где сумма подразумевается повторяющимися индексами вместо сигма-нотации Также часто ).

Свойства

Хотя Эйлер впервые представил эти уравнения в 1755 году, многие фундаментальные вопросы или концепции о них остаются без ответа.

В трех измерениях пространства в некоторых упрощенных сценариях уравнения Эйлера создают сингулярности.

Гладкие решения свободных (в смысле отсутствия исходного члена: g=0) уравнений удовлетворяют закону сохранения удельной кинетической энергии:

$${\partial \over \partial t}\left({\frac {1}{2}}u^{2}\right)+\nabla \cdot \left(u^{2}\mathbf {u} +w\mathbf {u} \right)=0$$

В одномерном случае без исходного члена (как градиента давления, так и внешней силы) уравнение количества движения становится невязким уравнением Бюргерса :

$${\partial u \over \partial t}+u{\partial u \over \partial x}=0$$

Это модельное уравнение дает много информации об уравнениях Эйлера.

Безразмерность

Смотрите также: уравнение импульса Коши § Безразмерность

Чтобы сделать уравнения безразмерными, характерная длина $r_{0}$, а характерная скорость $u_{0}$, необходимо определить. Их следует выбирать так, чтобы все безразмерные переменные были первого порядка. Таким образом, получаются следующие безразмерные переменные:

$${\begin{aligned}u^{*}&\equiv {\frac {u}{u_{0}}},&r^{*}&\equiv {\frac {r}{r_{0}}},\\[5pt]t^{*}&\equiv {\frac {u_{0}}{r_{0}}}t,&p^{*}&\equiv {\frac {w}{u_{0}^{2}}},\\[5pt]\nabla ^{*}&\equiv r_{0}\nabla \end{aligned}}$$

и единичного вектора поля :

$${\hat {\mathbf {g} }}\equiv {\frac {\mathbf {g} }{g}},$$

Подстановка этих обратных соотношений в уравнения Эйлера, определяющие число Фруда , дает (опуская * в вершине):

Уравнения Эйлера несжимаемой жидкости с постоянной и однородной плотностью
( безразмерная форма )

$\left\{{\begin{aligned}{D\mathbf {u} \over Dt}&=-\nabla w+{\frac {1}{\mathrm {Fr} }}{\hat {\mathbf {g} }}\\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.$

Уравнения Эйлера в пределе Фруда (отсутствие внешнего поля) называются свободными уравнениями и являются консервативными. Таким образом, предел высоких чисел Фруда (низкое внешнее поле) примечателен и может быть изучен с помощью теории возмущений .

Форма сохранения

См. Также: Уравнение сохранения.

Форма сохранения подчеркивает математические свойства уравнений Эйлера, и особенно сжатая форма часто является наиболее удобной для вычислительного моделирования гидродинамики . В вычислительном отношении использование сохраняющихся переменных дает некоторые преимущества. Это порождает большой класс численных методов.называемые консервативными методами.

Свободные уравнения Эйлера консервативны в том смысле, что они эквивалентны уравнению сохранения:

$${\frac {\partial \mathbf {y} }{\partial t}}+\nabla \cdot \mathbf {F} ={\mathbf {0} },$$

или просто в обозначениях Эйнштейна:

$${\frac {\partial y_{j}}{\partial t}}+{\frac {\partial f_{ij}}{\partial r_{i}}}=0_{i},$$

где сохраняющаяся величина $\mathbf {y}$ в данном случае является вектором, а $\mathbf {F}$ представляет собой матрицу потока . Это можно просто доказать.

показывать

Демонстрация формы консервации

First, the following identities hold:

$$\nabla \cdot (w\mathbf {I} )=\mathbf {I} \cdot \nabla w+w\nabla \cdot \mathbf {I} =\nabla w$$

$$\mathbf {u} \cdot \nabla \cdot \mathbf {u} =\nabla \cdot (\mathbf {u} \otimes \mathbf {u} )$$

where $\otimes$ denotes the outer product. The same identities expressed in Einstein notation are:

$$\partial _{i}\left(w\delta _{ij}\right)=\delta _{ij}\partial _{i}w+w\partial _{i}\delta _{ij}=\delta _{ij}\partial _{i}w=\partial _{j}w$$

$$u_{j}\partial _{i}u_{i}=\partial _{i}\left(u_{i}u_{j}\right)$$

where I is the identity matrix with dimension N and δ_ij its general element, the Kroenecker delta.

Thanks to these vector identities, the incompressible Euler equations with constant and uniform density and without external field can be put in the so-called conservation (or Eulerian) differential form, with vector notation:

$$\left\{{\begin{aligned}{\partial \mathbf {u} \over \partial t}+\nabla \cdot \left(\mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \right)&=\mathbf {0} \\{\partial 0 \over \partial t}+\nabla \cdot \mathbf {u} &=0,\end{aligned}}\right.$$

or with Einstein notation:

$$\left\{{\begin{aligned}\partial _{t}u_{j}+\partial _{i}\left(u_{i}u_{j}+w\delta _{ij}\right)&=0\\\partial _{t}0+\partial _{j}u_{j}&=0,\end{aligned}}\right.$$

Then incompressible Euler equations with uniform density have conservation variables:

$$\mathbf {y} ={\begin{pmatrix}\mathbf {u} \\0\end{pmatrix}};\qquad \mathbf {F} ={\begin{pmatrix}\mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \\\mathbf {u} \end{pmatrix}}.$$

Note that in the second component u is by itself a vector, with length N, so y has length N+1 and F has size N(N+1). In 3D for example y has length 4, I has size 3×3 and F has size 4×3, so the explicit forms are:

$${\mathbf {y} }={\begin{pmatrix}u_{1}\\u_{2}\\u_{3}\\0\end{pmatrix}};\quad {\mathbf {F} }={\begin{pmatrix}u_{1}^{2}+w&u_{1}u_{2}&u_{1}u_{3}\\u_{2}u_{1}&u_{2}^{2}+w&u_{2}u_{3}\\u_{3}u_{1}&u_{3}u_{2}&u_{3}^{2}+w\\u_{1}&u_{2}&u_{3}\end{pmatrix}}.$$

Наконец, уравнения Эйлера можно преобразовать в конкретное уравнение:

Уравнения Эйлера для несжимаемой жидкости с постоянной и однородной плотностью
( сохранение или эйлерова форма )

${\frac {\partial }{\partial t}}{\begin{pmatrix}\mathbf {u} \\0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {u} \otimes \mathbf {u} +w\mathbf {I} \\\mathbf {u} \end{pmatrix}}={\begin{pmatrix}\mathbf {g} \\0\end{pmatrix}}$

Пространственные размеры

Для некоторых задач, особенно при анализе течения сжимаемой жидкости в воздуховоде или в случае, если поток цилиндрически или сферически симметричен, одномерные уравнения Эйлера являются полезным первым приближением. Обычно уравнения Эйлера решаются Римана методом характеристик . Это предполагает нахождение кривых на плоскости независимых переменных (т.е. $x$ и $t$), вдоль которого уравнения в частных производных (ЧДУ) вырождаются в обыкновенные дифференциальные уравнения (ОДУ). Численные решения уравнений Эйлера во многом опираются на метод характеристик.

Эйлера

В конвективной форме уравнения Эйлера несжимаемой жидкости в случае переменной плотности в пространстве имеют вид:

Несжимаемые уравнения Эйлера
( конвективная или лагранжева форма )

$\left\{{\begin{aligned}{D\rho \over Dt}&=0\\{D\mathbf {u} \over Dt}&=-{\frac {\nabla p}{\rho }}+\mathbf {g} \\\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.$

где дополнительные переменные:

• $\rho$ жидкости - массовая плотность ,
• $p$ это давление , $p=\rho w$.

Первое уравнение, которое является новым, представляет собой уравнение неразрывности несжимаемой жидкости . Фактически общее уравнение непрерывности будет выглядеть так:

$${\partial \rho \over \partial t}+\mathbf {u} \cdot \nabla \rho +\rho \nabla \cdot \mathbf {u} =0$$

но здесь последний член тождественно равен нулю для ограничения несжимаемости.

Форма сохранения

См. Также: уравнение сохранения

Уравнения Эйлера для несжимаемой жидкости в пределе Фруда эквивалентны одному уравнению сохранения с сохраняющейся величиной и соответствующим потоком соответственно:

$$\mathbf {y} ={\begin{pmatrix}\rho \\\rho \mathbf {u} \\0\end{pmatrix}};\qquad {\mathbf {F} }={\begin{pmatrix}\rho \mathbf {u} \\\rho \mathbf {u} \otimes \mathbf {u} +p\mathbf {I} \\\mathbf {u} \end{pmatrix}}.$$

Здесь $\mathbf {y}$ имеет длину $N+2$ и $\mathbf {F}$ имеет размер $(N+2)N$. В общем случае (не только в пределе Фруда) уравнения Эйлера выражаются как:

$${\frac {\partial }{\partial t}}{\begin{pmatrix}\rho \\\rho \mathbf {u} \\0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\rho \mathbf {u} \\\rho \mathbf {u} \otimes \mathbf {u} +p\mathbf {I} \\\mathbf {u} \end{pmatrix}}={\begin{pmatrix}0\\\rho \mathbf {g} \\0\end{pmatrix}}$$

Переменные сохранения

Переменные для уравнений в форме сохранения еще не оптимизированы. Фактически мы могли бы определить:

$${\mathbf {y} }={\begin{pmatrix}\rho \\\mathbf {j} \\0\end{pmatrix}};\qquad {\mathbf {F} }={\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\,\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\{\frac {\mathbf {j} }{\rho }}\end{pmatrix}}.$$

где $\mathbf {j} =\rho \mathbf {u}$ — плотность импульса , переменная сохранения.

Уравнения Эйлера для несжимаемой жидкости
( сохранение или эйлерова форма )

${\frac {\partial }{\partial t}}{\begin{pmatrix}\rho \\\mathbf {j} \\0\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\,\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\{\frac {\mathbf {j} }{\rho }}\end{pmatrix}}={\begin{pmatrix}0\\\mathbf {f} \\0\end{pmatrix}}$

где $\mathbf {f} =\rho \mathbf {g}$ — плотность силы , переменная сохранения.

Уравнения Эйлера

В дифференциально-конвективной форме сжимаемые (и наиболее общие) уравнения Эйлера можно коротко записать с использованием обозначения материальной производной :

Уравнения Эйлера
( конвективная форма )

$\left\{{\begin{aligned}{D\rho \over Dt}&=-\rho \nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=-{\frac {\nabla p}{\rho }}+\mathbf {g} \\[1.2ex]{De \over Dt}&=-{\frac {p}{\rho }}\nabla \cdot \mathbf {u} \end{aligned}}\right.$

где дополнительные переменные здесь:

• $e$ – удельная внутренняя энергия (внутренняя энергия единицы массы).

Таким образом, приведенные выше уравнения представляют сохранение массы , импульса и энергии : уравнение энергии, выраженное в переменной внутренней энергии, позволяет понять связь с несжимаемым случаем, но это не в самой простой форме.Массовая плотность, скорость потока и давление являются так называемыми конвективными переменными (или физическими переменными, или лагранжевыми переменными), тогда как плотность массы, плотность импульса и полная плотность энергии являются так называемыми сохраняющимися переменными (также называемыми эйлеровыми или математическими переменными). .

Если расширить производную материала, приведенные выше уравнения будут следующими:

$$\left\{{\begin{aligned}{\partial \rho \over \partial t}+\mathbf {u} \cdot \nabla \rho +\rho \nabla \cdot \mathbf {u} &=0\\[1.2ex]{\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} +{\frac {\nabla p}{\rho }}&=\mathbf {g} \\[1.2ex]{\partial e \over \partial t}+\mathbf {u} \cdot \nabla e+{\frac {p}{\rho }}\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.$$

Несжимаемое ограничение (ещё раз)

Возвращаясь к несжимаемому случаю, теперь становится очевидным, что несжимаемая связь, типичная для первых случаев, на самом деле представляет собой особую, справедливую для несжимаемых потоков форму уравнения энергии , а не уравнения массы. В частности, несжимаемая связь соответствует следующему очень простому уравнению энергии:

$${\frac {De}{Dt}}=0$$

Таким образом, для несжимаемой невязкой жидкости удельная внутренняя энергия постоянна вдоль линий тока , в том числе и в потоке, зависящем от времени. Давление в несжимаемом потоке действует как множитель Лагранжа , являясь множителем несжимаемой связи в уравнении энергии, и, следовательно, в несжимаемых потоках оно не имеет термодинамического смысла. Фактически термодинамика типична для сжимаемых течений и вырождается в несжимаемые течения.

Основываясь на уравнении сохранения массы, это уравнение можно представить в виде сохранения:

$${\partial \rho e \over \partial t}+\nabla \cdot (\rho e\mathbf {u} )=0$$

это означает, что для несжимаемого невязкого непроводящего потока справедливо уравнение неразрывности внутренней энергии.

Сохранение энтальпии

Поскольку по определению удельная энтальпия равна:

$$h=e+{\frac {p}{\rho }}$$

Материальную производную удельной внутренней энергии можно выразить как:

$${De \over Dt}={Dh \over Dt}-{\frac {1}{\rho }}\left({Dp \over Dt}-{\frac {p}{\rho }}{D\rho \over Dt}\right)$$

Тогда, подставив уравнение импульса в это выражение, получим:

$${De \over Dt}={Dh \over Dt}-{\frac {1}{\rho }}\left(p\nabla \cdot \mathbf {u} +{Dp \over Dt}\right)$$

И подставив последнее в уравнение энергии, получим, что выражение энтальпии для уравнения энергии Эйлера:

$${Dh \over Dt}={\frac {1}{\rho }}{Dp \over Dt}$$

В системе отсчета, движущейся с невязким и непроводящим потоком, изменение энтальпии напрямую соответствует изменению давления.

Термодинамика идеальных жидкостей

В термодинамике независимыми переменными являются удельный объем и удельная энтропия , а удельная энергия является функцией состояния этих двух переменных.

показывать

Вывод формы, справедливой для термодинамических систем

Considering the first equation, variable must be changed from density to specific volume. By definition:

$$v\equiv {\frac {1}{\rho }}$$

Thus the following identities hold:

$$\nabla \rho =\nabla \left({\frac {1}{v}}\right)=-{\frac {1}{v^{2}}}\nabla v$$

$${\frac {\partial \rho }{\partial t}}={\frac {\partial }{\partial t}}\left({\frac {1}{v}}\right)=-{\frac {1}{v^{2}}}{\frac {\partial v}{\partial t}}$$

Then by substituting these expressions in the mass conservation equation:

$$-{\frac {\mathbf {u} }{v^{2}}}\cdot \nabla v-{\frac {1}{v^{2}}}{\frac {\partial v}{\partial t}}=-{\frac {1}{v}}\nabla \cdot \mathbf {u}$$

And by multiplication:

$${\partial v \over \partial t}+\mathbf {u} \cdot \nabla v=v\nabla \cdot \mathbf {u}$$

This equation is the only belonging to general continuum equations, so only this equation have the same form for example also in Navier-Stokes equations.

On the other hand, the pressure in thermodynamics is the opposite of the partial derivative of the specific internal energy with respect to the specific volume:

$$p(v,s)=-{\partial e(v,s) \over \partial v}$$

since the internal energy in thermodynamics is a function of the two variables aforementioned, the pressure gradient contained into the momentum equation should be explicited as:

$$-\nabla p(v,s)=-{\frac {\partial p}{\partial v}}\nabla v-{\frac {\partial p}{\partial s}}\nabla s={\frac {\partial ^{2}e}{\partial v^{2}}}\nabla v+{\frac {\partial ^{2}e}{\partial v\partial s}}\nabla s$$

It is convenient for brevity to switch the notation for the second order derivatives:

$$-\nabla p(v,s)=e_{vv}\nabla v+e_{vs}\nabla s$$

Finally, the energy equation:

$${De \over Dt}=-pv\nabla \cdot \mathbf {u}$$

can be further simplified in convective form by changing variable from specific energy to the specific entropy: in fact the first law of thermodynamics in local form can be written:

$${De \over Dt}=T{Ds \over Dt}-p{Dv \over Dt}$$

by substituting the material derivative of the internal energy, the energy equation becomes:

$$T{Ds \over Dt}+{\frac {p}{\rho ^{2}}}\left({D\rho \over Dt}+\rho \nabla \cdot \mathbf {u} \right)=0$$

now the term between parenthesis is identically zero according to the conservation of mass, then the Euler energy equation becomes simply:

$${Ds \over Dt}=0$$

Следовательно, для термодинамической жидкости уравнения Эйлера для сжимаемой жидкости лучше всего записать как:

Уравнения Эйлера
( конвективная форма для термодинамической системы )

$\left\{{\begin{aligned}{Dv \over Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=ve_{vv}\nabla v+ve_{vs}\nabla s+\mathbf {g} \\[1.2ex]{Ds \over Dt}&=0\end{aligned}}\right.$

где:

• $v$ это удельный объем
• $\mathbf {u}$ вектор скорости потока
• $s$ это удельная энтропия

В общем случае, а не только в несжимаемом случае, уравнение энергии означает, что для невязкой термодинамической жидкости удельная энтропия постоянна вдоль линий тока , в том числе и в потоке, зависящем от времени. Основываясь на уравнении сохранения массы, это уравнение можно представить в виде сохранения:

$${\partial \rho s \over \partial t}+\nabla \cdot (\rho s\mathbf {u} )=0$$

это означает, что для невязкого непроводящего потока справедливо уравнение неразрывности для энтропии.

С другой стороны, две частные производные удельной внутренней энергии второго порядка в уравнении количества движения требуют указания фундаментального уравнения состояния рассматриваемого материала, т.е. удельной внутренней энергии как функции двух переменных: удельного объема и удельная энтропия:

$$e=e(v,s)$$

Фундаментальное : уравнение состояния содержит всю термодинамическую информацию о системе (Каллен, 1985) точно так же, как пара теплового уравнения состояния вместе с калорическим уравнением состояния.

Форма сохранения

См. Также: Уравнение сохранения.

Уравнения Эйлера в пределе Фруда эквивалентны одному уравнению сохранения с сохраняющейся величиной и соответствующим потоком соответственно:

$$\mathbf {y} ={\begin{pmatrix}\rho \\\mathbf {j} \\E^{t}\end{pmatrix}};\qquad {\mathbf {F} }={\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\\left(E^{t}+p\right){\frac {1}{\rho }}\mathbf {j} \end{pmatrix}}.$$

где:

• $\mathbf {j} =\rho \mathbf {u}$ — плотность импульса , переменная сохранения.
• ${\textstyle E^{t}=\rho e+{\frac {1}{2}}\rho u^{2}}$ - полная плотность энергии (полная энергия на единицу объема).

Здесь $\mathbf {y}$ имеет длину N + 2 и $\mathbf {F}$ имеет размер N(N + 2). В общем случае (не только в пределе Фруда) уравнения Эйлера выражаются как:

Уравнение (я) Эйлера
( исходное сохранение или эйлерова форма )

${\frac {\partial }{\partial t}}{\begin{pmatrix}\rho \\\mathbf {j} \\E^{t}\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\\left(E^{t}+p\right){\frac {1}{\rho }}\mathbf {j} \end{pmatrix}}={\begin{pmatrix}0\\\mathbf {f} \\{\frac {1}{\rho }}\mathbf {j} \cdot \mathbf {f} \end{pmatrix}}$

где $\mathbf {f} =\rho \mathbf {g}$ — плотность силы , переменная сохранения.

Заметим, что уравнение Эйлера, даже если оно консервативно (отсутствие внешнего поля, предел Фруда), не имеет инвариантов Римана . вообще говоря, Требуются некоторые дополнительные предположения

Однако мы уже упоминали, что для термодинамической жидкости уравнение полной плотности энергии эквивалентно уравнению сохранения:

$${\partial \over \partial t}(\rho s)+\nabla \cdot (\rho s\mathbf {u} )=0$$

Тогда уравнения сохранения в случае термодинамической жидкости проще выражаются так:

Уравнение (я) Эйлера
( форма сохранения для термодинамических жидкостей )

${\frac {\partial }{\partial t}}{\begin{pmatrix}\rho \\\mathbf {j} \\S\end{pmatrix}}+\nabla \cdot {\begin{pmatrix}\mathbf {j} \\{\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +p\mathbf {I} \\S{\frac {\mathbf {j} }{\rho }}\end{pmatrix}}={\begin{pmatrix}0\\\mathbf {f} \\0\end{pmatrix}}$

где $S=\rho s$ — плотность энтропии, термодинамическая переменная сохранения.

Другая возможная форма уравнения энергии, особенно полезная для изобар :

$${\frac {\partial H^{t}}{\partial t}}+\nabla \cdot \left(H^{t}\mathbf {u} \right)=\mathbf {u} \cdot \mathbf {f} -{\frac {\partial p}{\partial t}}$$

где ${\textstyle H^{t}=E^{t}+p=\rho e+p+{\frac {1}{2}}\rho u^{2}}$ - плотность полной энтальпии .

Квазилинейная форма

Расширение потоков может быть важной частью построения численных решателей , например, путем использования ( приблизительных ) решений задачи Римана . В областях, где вектор состояния y изменяется плавно, уравнения в консервативной форме можно привести к квазилинейной форме:

$${\frac {\partial \mathbf {y} }{\partial t}}+\mathbf {A} _{i}{\frac {\partial \mathbf {y} }{\partial r_{i}}}={\mathbf {0} }.$$

где $\mathbf {A} _{i}$ называются якобианами потока, определяемыми как матрицы :

$$\mathbf {A} _{i}(\mathbf {y} )={\frac {\partial \mathbf {f} _{i}(\mathbf {y} )}{\partial \mathbf {y} }}.$$

Очевидно, что этот якобиан не существует в областях разрывов (например, контактных разрывов, ударных волн в невязких непроводящих потоках). Если поток якобианов $\mathbf {A} _{i}$ не являются функциями вектора состояния $\mathbf {y}$, уравнения оказываются линейными .

Характеристические уравнения

Сжимаемые уравнения Эйлера можно разделить на набор волновых уравнений N+2, который описывает звук в эйлеровом континууме, если они выражены в характеристических переменных вместо сохраняющихся переменных.

На самом деле тензор A всегда диагонализуем . Если все собственные значения (в случае уравнений Эйлера) действительны, система определяется как гиперболическая , а физически собственные значения представляют собой скорости распространения информации. Если они все различены, система определяется строго гиперболической (будет доказано, что это случай одномерных уравнений Эйлера). Более того, диагонализацию уравнения Эйлера для сжимаемой жидкости легче провести, когда уравнение энергии выражается в переменной энтропии (т.е. с помощью уравнений для термодинамических жидкостей), чем в других переменных энергии. Это станет ясно, если рассмотреть случай 1D.

Если $\mathbf {p} _{i}$ — правый собственный вектор матрицы $\mathbf {A}$ соответствующее собственному значению $\lambda _{i}$, построив матрицу проекции :

$$\mathbf {P} =\left[\mathbf {p} _{1},\mathbf {p} _{2},...,\mathbf {p} _{n}\right]$$

Наконец, можно найти характеристические переменные как:

$$\mathbf {w} =\mathbf {P} ^{-1}\mathbf {y} ,$$

Поскольку A является постоянным, умножение исходного одномерного уравнения в поток-якобианской форме на P ⁻¹ дает характеристические уравнения:

$${\frac {\partial w_{i}}{\partial t}}+\lambda _{j}{\frac {\partial w_{i}}{\partial r_{j}}}=0_{i}$$

Исходные уравнения были разделены на N+2 характеристических уравнения, каждое из которых описывает простую волну, причем собственные значения представляют собой скорости волн. Переменные w _i называются характеристическими переменными и представляют собой подмножество консервативных переменных. Наконец, решение задачи начального значения в терминах характеристических переменных оказывается очень простым. В одном пространственном измерении это:

$$w_{i}(x,t)=w_{i}\left(x-\lambda _{i}t,0\right)$$

Тогда решение в терминах исходных консервативных переменных получается путем обратного преобразования:

$$\mathbf {y} =\mathbf {P} \mathbf {w} ,$$

это вычисление можно представить как линейную комбинацию собственных векторов:

$$\mathbf {y} (x,t)=\sum _{i=1}^{m}w_{i}\left(x-\lambda _{i}t,0\right)\mathbf {p} _{i},$$

Теперь становится очевидным, что характеристические переменные действуют как веса в линейной комбинации собственных векторов Якобиана. Решение можно рассматривать как суперпозицию волн, каждая из которых адвектируется независимо без изменения формы. Каждая i -я волна имеет форму w _i pi _и скорость распространения λ _i . Ниже мы покажем очень простой пример этой процедуры решения.

Волны в одномерной невязкой

Если рассматривать уравнения Эйлера для термодинамической жидкости с двумя дополнительными предположениями об одном пространственном измерении и свободе (отсутствие внешнего поля: g = 0):

$$\left\{{\begin{aligned}{\partial v \over \partial t}+u{\partial v \over \partial x}-v{\partial u \over \partial x}&=0\\[1.2ex]{\partial u \over \partial t}+u{\partial u \over \partial x}-e_{vv}v{\partial v \over \partial x}-e_{vs}v{\partial s \over \partial x}&=0\\[1.2ex]{\partial s \over \partial t}+u{\partial s \over \partial x}&=0\end{aligned}}\right.$$

Если определить вектор переменных:

$$\mathbf {y} ={\begin{pmatrix}v\\u\\s\end{pmatrix}}$$

напоминая, что $v$ это удельный объем, $u$ скорость потока, $s$ удельная энтропия, соответствующая матрица Якобиана:

$${\mathbf {A} }={\begin{pmatrix}u&-v&0\\-e_{vv}v&u&-e_{vs}v\\0&0&u\end{pmatrix}}.$$

Сначала необходимо найти собственные значения этой матрицы, решив характеристическое уравнение :

$$\det(\mathbf {A} (\mathbf {y} )-\lambda (\mathbf {y} )\mathbf {I} )=0$$

это явно:

$$\det {\begin{bmatrix}u-\lambda &-v&0\\-e_{vv}v&u-\lambda &-e_{vs}v\\0&0&u-\lambda \end{bmatrix}}=0$$

Этот определитель очень прост: самые быстрые вычисления начинаются с последней строки, поскольку в ней наибольшее количество нулевых элементов.

$$(u-\lambda )\det {\begin{bmatrix}u-\lambda &-v\\-e_{vv}v&u-\lambda \end{bmatrix}}=0$$

Теперь, вычислив определитель 2×2:

$$(u-\lambda )\left((u-\lambda )^{2}-e_{vv}v^{2}\right)=0$$

определив параметр:

$$a(v,s)\equiv v{\sqrt {e_{vv}}}$$

или, что эквивалентно, в механических переменных, например:

$$a(\rho ,p)\equiv {\sqrt {\partial p \over \partial \rho }}$$

Этот параметр всегда действителен согласно второму закону термодинамики . Фактически второй закон термодинамики можно выразить несколькими постулатами. Самым элементарным из них в математическом плане является утверждение о выпуклости фундаментального уравнения состояния, т.е. матрицы Гессе удельной энергии, выраженной как функция удельного объема и удельной энтропии:

$${\begin{pmatrix}e_{vv}&e_{vs}\\e_{vs}&e_{ss}\end{pmatrix}}$$

определяется положительно. Это утверждение соответствует двум условиям:

$$\left\{{\begin{aligned}e_{vv}&>0\\[1.2ex]e_{vv}e_{ss}-e_{vs}^{2}&>0\end{aligned}}\right.$$

Первое условие гарантирует, что параметр a определен как действительный.

В конечном итоге характеристическое уравнение дает:

$$(u-\lambda )\left((u-\lambda )^{2}-a^{2}\right)=0$$

Это имеет три реальных решения:

$$\lambda _{1}(v,u,s)=u-a(v,s)\quad \lambda _{2}(u)=u,\quad \lambda _{3}(v,u,s)=u+a(v,s)$$

Тогда матрица имеет три действительных собственных значения, все из которых различаются: одномерные уравнения Эйлера представляют собой строго гиперболическую систему .

На этом этапе необходимо определить три собственных вектора: каждый из них получается путем подстановки одного собственного значения в уравнение собственных значений и последующего его решения. Подставив первое собственное значение λ _1, получим:

$${\begin{pmatrix}a&-v&0\\-e_{vv}v&a&-e_{vs}v\\0&0&a\end{pmatrix}}{\begin{pmatrix}v_{1}\\u_{1}\\s_{1}\end{pmatrix}}=0$$

На основе третьего уравнения, которое просто имеет решение s ₁ =0, система сводится к:

$${\begin{pmatrix}a&-v\\-a^{2}/v&a\end{pmatrix}}{\begin{pmatrix}v_{1}\\u_{1}\end{pmatrix}}=0$$

Эти два уравнения, как обычно, избыточны, тогда собственный вектор определяется с помощью умножающей константы. Выбираем в качестве правого собственного вектора:

$$\mathbf {p} _{1}={\begin{pmatrix}v\\a\\0\end{pmatrix}}$$

Два других собственных вектора можно найти аналогичной процедурой:

$$\mathbf {p} _{2}={\begin{pmatrix}e_{vs}\\0\\-\left({\frac {a}{v}}\right)^{2}\end{pmatrix}},\qquad \mathbf {p} _{3}={\begin{pmatrix}v\\-a\\0\end{pmatrix}}$$

Тогда можно построить матрицу проекции:

$$\mathbf {P} (v,u,s)=(\mathbf {p} _{1},\mathbf {p} _{2},\mathbf {p} _{3})={\begin{pmatrix}v&e_{vs}&v\\a&0&-a\\0&-\left({\frac {a}{v}}\right)^{2}&0\end{pmatrix}}$$

Наконец, становится очевидным, что действительный параметр a, определенный ранее, представляет собой скорость распространения информационной характеристики гиперболической системы, составленной из уравнений Эйлера, т. е. это скорость волны . Осталось показать, что скорость звука соответствует частному случаю изэнтропического преобразования :

$$a_{s}\equiv {\sqrt {\left({\partial p \over \partial \rho }\right)_{s}}}$$

и

Скорость звука определяется как скорость волны изэнтропического преобразования:

$$a_{s}(\rho ,p)\equiv {\sqrt {\left({\partial p \over \partial \rho }\right)_{s}}}$$

по определению изоэнтропической сжимаемости:

$$K_{s}(\rho ,p)\equiv \rho \left({\partial p \over \partial \rho }\right)_{s}$$

скорость звука всегда представляет собой квадратный корень из отношения изэнтропической сжимаемости к плотности:

$$a_{s}\equiv {\sqrt {\frac {K_{s}}{\rho }}}$$

Идеальный газ

Скорость звука в идеальном газе зависит только от его температуры:

$$a_{s}(T)={\sqrt {\gamma {\frac {T}{m}}}}$$

показывать

Вывод вида, справедливый для идеальных газов

In an ideal gas the isoentropic transformation is described by the Poisson's law:

$$d\left(p\rho ^{-\gamma }\right)_{s}=0$$

where γ is the heat capacity ratio, a constant for the material. By explicitating the differentials:

$$\rho ^{-\gamma }(dp)_{s}+\gamma p\rho ^{-\gamma -1}(d\rho )_{s}=0$$

and by dividing for ρ^−γ dρ:

$$\left({\partial p \over \partial \rho }\right)_{s}=\gamma p\rho$$

Then by substitution in the general definitions for an ideal gas the isentropic compressibility is simply proportional to the pressure:

$$K_{s}(p)=\gamma p$$

and the sound speed results (Newton–Laplace law):

$$a_{s}(\rho ,p)={\sqrt {\gamma {\frac {p}{\rho }}}}$$

Notably, for an ideal gas the ideal gas law holds, that in mathematical form is simply:

$$p=nT$$

where n is the number density, and T is the absolute temperature, provided it is measured in energetic units (i.e. in joules) through multiplication with the Boltzmann constant. Since the mass density is proportional to the number density through the average molecular mass m of the material:

$$\rho =mn$$

The ideal gas law can be recast into the formula:

$${\frac {p}{\rho }}={\frac {T}{m}}$$

By substituting this ratio in the Newton–Laplace law, the expression of the sound speed into an ideal gas as function of temperature is finally achieved.

Поскольку удельная энтальпия идеального газа пропорциональна его температуре:

$$h=c_{p}T={\frac {\gamma }{\gamma -1}}{\frac {T}{m}}$$

скорость звука в идеальном газе также можно поставить в зависимость только от его удельной энтальпии:

$$a_{s}(h)={\sqrt {(\gamma -1)h}}$$

Бернулли для устойчивого

Теорема Бернулли является прямым следствием уравнений Эйлера.

Несжимаемый случай и форма Лэмба

Тождество векторного исчисления векторного произведения ротора имеет место:

$$\mathbf {v\ \times } \left(\mathbf {\nabla \times F} \right)=\nabla _{F}\left(\mathbf {v\cdot F} \right)-\mathbf {v\cdot \nabla } \mathbf {F} \ ,$$

где индекс Фейнмана $\nabla _{F}$ используется, что означает, что индексированный градиент действует только на фактор $\mathbf {F}$.

Лэмб в своей знаменитой классической книге «Гидродинамика» (1895 г.), которая все еще издается, использовал это тождество для изменения конвективного члена скорости потока в вращательной форме:

$$\mathbf {u} \cdot \nabla \mathbf {u} ={\frac {1}{2}}\nabla \left(u^{2}\right)+(\nabla \times \mathbf {u} )\times \mathbf {u}$$

уравнение количества движения Эйлера в форме Лэмба принимает вид:

$${\frac {\partial \mathbf {u} }{\partial t}}+{\frac {1}{2}}\nabla \left(u^{2}\right)+(\nabla \times \mathbf {u} )\times \mathbf {u} +{\frac {\nabla p}{\rho }}=\mathbf {g} ={\frac {\partial \mathbf {u} }{\partial t}}+{\frac {1}{2}}\nabla \left(u^{2}\right)-\mathbf {u} \times (\nabla \times \mathbf {u} )+{\frac {\nabla p}{\rho }}$$

Смотрите также: уравнение импульса Коши § Форма Лэмба

Теперь, основываясь на другом тождестве:

$$\nabla \left({\frac {p}{\rho }}\right)={\frac {\nabla p}{\rho }}-{\frac {p}{\rho ^{2}}}\nabla \rho$$

уравнение количества движения Эйлера принимает форму, оптимальную для демонстрации теоремы Бернулли для установившихся потоков:

$$\nabla \left({\frac {1}{2}}u^{2}+{\frac {p}{\rho }}\right)-\mathbf {g} =-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )-{\frac {\partial \mathbf {u} }{\partial t}}$$

Действительно, в случае внешнего консервативного поля , определив его потенциал φ:

$$\nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)=-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )-{\frac {\partial \mathbf {u} }{\partial t}}$$

В случае установившегося течения производная скорости потока по времени исчезает, поэтому уравнение количества движения принимает вид:

$$\nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)=-{\frac {p}{\rho ^{2}}}\nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u} )$$

А при проектировании уравнения количества движения на направление потока, т. е. вдоль линии тока , векторное произведение исчезает, поскольку его результат всегда перпендикулярен скорости:

$$\mathbf {u} \cdot \nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)=-{\frac {p}{\rho ^{2}}}\mathbf {u} \cdot \nabla \rho$$

В устойчивом несжимаемом случае уравнение массы имеет простой вид:

$$\mathbf {u} \cdot \nabla \rho =0,$$

то есть закон сохранения массы для устойчивого несжимаемого потока утверждает, что плотность вдоль линии тока постоянна . Тогда уравнение количества движения Эйлера в стационарном несжимаемом случае принимает вид:

$$\mathbf {u} \cdot \nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)=0$$

удобство определения полного напора Теперь очевидно для потока невязкой жидкости:

$$b_{l}\equiv {\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }},$$

что можно просто записать как:

$$\mathbf {u} \cdot \nabla b_{l}=0$$

То есть баланс импульсов для устойчивого невязкого и несжимаемого течения во внешнем консервативном поле утверждает, что общий напор вдоль линии тока постоянен .

Сжимаемый корпус

В наиболее общем стационарном (сжимаемом) случае уравнение массы в форме сохранения имеет вид:

$$\nabla \cdot \mathbf {j} =\rho \nabla \cdot \mathbf {u} +\mathbf {u} \cdot \nabla \rho =0.$$

Поэтому предыдущее выражение скорее

$$\mathbf {u} \cdot \nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)={\frac {p}{\rho }}\nabla \cdot \mathbf {u}$$

Правая часть появляется в уравнении энергии в конвективной форме, которая в установившемся состоянии выглядит следующим образом:

$$\mathbf {u} \cdot \nabla e=-{\frac {p}{\rho }}\nabla \cdot \mathbf {u}$$

Таким образом, уравнение энергии принимает вид:

$$\mathbf {u} \cdot \nabla \left(e+{\frac {p}{\rho }}+{\frac {1}{2}}u^{2}+\phi \right)=0,$$

так что внутренняя удельная энергия теперь проявляется в голове.

Поскольку потенциал внешнего поля обычно мал по сравнению с остальными членами, последние удобно сгруппировать в общую энтальпию :

$$h^{t}\equiv e+{\frac {p}{\rho }}+{\frac {1}{2}}u^{2}$$

а инвариант Бернулли для потока невязкого газа:

$$b_{g}\equiv h^{t}+\phi =b_{l}+e,$$

что можно записать как:

$$\mathbf {u} \cdot \nabla b_{g}=0$$

То есть баланс энергии для стационарного невязкого течения во внешнем консервативном поле утверждает, что сумма полной энтальпии и внешнего потенциала постоянна вдоль линии тока .

В обычном случае небольшого потенциального поля просто:

$$\mathbf {u} \cdot \nabla h^{t}\sim 0$$

Форма Фридмана

Смотрите также: теорема Крокко

Заменяя градиент давления градиентом энтропии и энтальпии, согласно первому закону термодинамики в энтальпийной форме:

$$v\nabla p=-T\nabla s+\nabla h$$

в конвективной форме уравнения количества движения Эйлера получаем:

$${\frac {D\mathbf {u} }{Dt}}=T\nabla \,s-\nabla \,h$$

Фридман вывел это уравнение для частного случая идеального газа и опубликовал его в 1922 году. Однако это уравнение является общим для невязкой непроводящей жидкости и ни одно уравнение состояния в нем не является неявным.

С другой стороны, подставляя энтальпийную форму первого закона термодинамики во вращательную форму уравнения количества движения Эйлера, получаем:

$${\frac {\partial \mathbf {u} }{\partial t}}+{\frac {1}{2}}\nabla \left(u^{2}\right)+(\nabla \times \mathbf {u} )\times \mathbf {u} +{\frac {\nabla p}{\rho }}=\mathbf {g}$$

и определив удельную полную энтальпию:

$$h^{t}=h+{\frac {1}{2}}u^{2}$$

приходим к форме Крокко – Вассони (Крокко, 1937) уравнения количества движения Эйлера:

$${\frac {\partial \mathbf {u} }{\partial t}}+(\nabla \times \mathbf {u} )\times \mathbf {u} -T\nabla s+\nabla h^{t}=\mathbf {g}$$

В устойчивом случае две переменные, энтропия и полная энтальпия, особенно полезны, поскольку уравнения Эйлера можно преобразовать в форму Крокко:

$$\left\{{\begin{aligned}\mathbf {u} \times \nabla \times \mathbf {u} +T\nabla s-\nabla h^{t}&=\mathbf {g} \\\mathbf {u} \cdot \nabla s&=0\\\mathbf {u} \cdot \nabla h^{t}&=0\end{aligned}}\right.$$

Наконец, если поток также изотермический:

$$T\nabla s=\nabla (Ts)$$

определив удельную полную свободную энергию Гиббса :

$$g^{t}\equiv h^{t}+Ts$$

форму Крокко можно свести к:

$$\left\{{\begin{aligned}\mathbf {u} \times \nabla \times \mathbf {u} -\nabla g^{t}&=\mathbf {g} \\\mathbf {u} \cdot \nabla g^{t}&=0\end{aligned}}\right.$$

Из этих соотношений можно сделать вывод, что удельная полная свободная энергия однородна в стационарном, безвихревом, изотермическом, изоэнтропическом, невязком потоке.

Разрывы

См. Также: Ударные волны и уравнение Бюргерса.

Уравнения Эйлера — квазилинейные гиперболические уравнения, а их общие решения — волны . При определенных предположениях их можно упростить, приведя к уравнению Бюргерса . Подобно знакомым океанским волнам , волны, описываемые уравнениями Эйлера, «разбиваются» так называемые ударные волны и образуются ; это нелинейный эффект, который означает, что решение становится многозначным . Физически это представляет собой отказ от предположений, которые привели к формулировке дифференциальных уравнений, и для извлечения дополнительной информации из уравнений мы должны вернуться к более фундаментальной интегральной форме. Затем формулируются слабые решения путем обработки «скачков» (разрывов) величин потока – плотности, скорости, давления, энтропии – с использованием уравнений Рэнкина – Гюгонио . Физические величины редко бывают прерывистыми; в реальных течениях эти разрывы сглаживаются вязкостью и теплообменом . (См. уравнения Навье – Стокса )

Распространение ударной волны изучается, среди многих других областей, в аэродинамике и ракетном движении , где возникают достаточно быстрые потоки.

Чтобы правильно вычислить величины континуума в разрывных зонах (например, ударных волнах или пограничных слоях) из локальных форм. (все вышеперечисленные формы являются локальными формами, поскольку описываемые переменные типичны для одной точки рассматриваемого пространства, т.е. являются локальными переменными ) уравнений Эйлера с помощью методов конечных разностей, как правило, слишком много точек пространства и временных шагов было бы необходимо для память компьютеров сейчас и в ближайшем будущем. В этих случаях необходимо избегать локальных форм уравнений сохранения, передавая некоторые слабые формы , такие как форма конечного объема .

–

Начиная с простейшего случая, рассмотрим стационарное свободное уравнение сохранения в форме сохранения в пространственной области:

$$\nabla \cdot \mathbf {F} =\mathbf {0}$$

где вообще F — матрица потока. Путем интегрирования этого локального уравнения по фиксированному объему V _m получим:

$$\int _{V_{m}}\nabla \cdot \mathbf {F} \,dV=\mathbf {0} .$$

Тогда, опираясь на теорему о расходимости , можно преобразовать этот интеграл в граничный интеграл от потока:

$$\oint _{\partial V_{m}}\mathbf {F} \,ds=\mathbf {0} .$$

Эта глобальная форма просто утверждает, что не существует чистого потока сохраняющейся величины, проходящей через область в устойчивом случае и без источника. В 1D объем сводится к интервалу , его граница является его экстремумами, тогда теорема о дивергенции сводится к фундаментальной теореме исчисления :

$$\int _{x_{m}}^{x_{m+1}}\mathbf {F} (x')\,dx'=\mathbf {0} ,$$

это простое конечно-разностное уравнение , известное как соотношение скачка :

$$\Delta \mathbf {F} =\mathbf {0} .$$

Это можно выразить явно так:

$$\mathbf {F} _{m+1}-\mathbf {F} _{m}=\mathbf {0}$$

где используются обозначения:

$$\mathbf {F} _{m}=\mathbf {F} (x_{m}).$$

Или, если выполнить неопределенный интеграл:

$$\mathbf {F} -\mathbf {F} _{0}=\mathbf {0} .$$

С другой стороны, переходное уравнение сохранения:

$${\partial y \over \partial t}+\nabla \cdot \mathbf {F} =\mathbf {0}$$

приводит к отношению перехода:

$${\frac {dx}{dt}}\,\Delta u=\Delta \mathbf {F} .$$

Для одномерных уравнений Эйлера переменными сохранения и потоком являются векторы:

$$\mathbf {y} ={\begin{pmatrix}{\frac {1}{v}}\\j\\E^{t}\end{pmatrix}},$$

$$\mathbf {F} ={\begin{pmatrix}j\\vj^{2}+p\\vj\left(E^{t}+p\right)\end{pmatrix}},$$

где:

• $v$ это удельный объем,
• $j$ это поток массы.

В одномерном случае соответствующие соотношения скачков, называемые уравнениями Рэнкина–Гюгонио , имеют вид:

$$\left\{{\begin{aligned}{\frac {dx}{dt}}\Delta \left({\frac {1}{v}}\right)&=\Delta j\\[1.2ex]{\frac {dx}{dt}}\Delta j&=\Delta (vj^{2}+p)\\[1.2ex]{\frac {dx}{dt}}\Delta E^{t}&=\Delta (jv(E^{t}+p)).\end{aligned}}\right.$$

В устойчивом одномерном случае это выглядит просто:

$$\left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0\\[1.2ex]\Delta \left(j\left({\frac {E^{t}}{\rho }}+{\frac {p}{\rho }}\right)\right)&=0.\end{aligned}}\right.$$

Благодаря уравнению разности масс уравнение разности энергий можно упростить без каких-либо ограничений:

$$\left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0\\[1.2ex]\Delta h^{t}&=0\end{aligned}}\right.,$$

где $h^{t}$ – удельная полная энтальпия.

Обычно они выражаются в конвективных переменных:

$$\left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left({\frac {u^{2}}{v}}+p\right)&=0\\[1.2ex]\Delta \left(e+{\frac {1}{2}}u^{2}+pv\right)&=0,\end{aligned}}\right.$$

где:

• $u$ это скорость потока
• $e$ – удельная внутренняя энергия.

Уравнение энергии представляет собой интегральную форму уравнения Бернулли в сжимаемом случае. Прежние уравнения массы и импульса путем замены приводят к уравнению Рэлея:

$${\frac {\Delta p}{\Delta v}}=-{\frac {u_{0}^{2}}{v_{0}}}.$$

Поскольку второй член является константой, уравнение Рэлея всегда описывает простую линию в плоскости давления-объема, не зависящую от какого-либо уравнения состояния, т. е. линию Рэлея . Путем подстановки в уравнения Рэнкина – Гюгонио это также можно выразить явно следующим образом:

$$\left\{{\begin{aligned}\rho u&=\rho _{0}u_{0}\\[1.2ex]\rho u^{2}+p&=\rho _{0}u_{0}^{2}+p_{0}\\[1.2ex]e+{\frac {1}{2}}u^{2}+{\frac {p}{\rho }}&=e_{0}+{\frac {1}{2}}u_{0}^{2}+{\frac {p_{0}}{\rho _{0}}}.\end{aligned}}\right.$$

Можно также получить кинетическое уравнение и к уравнению Гюгонио. Аналитические отрывки здесь не приводятся для краткости.

См. Также: уравнение Рэлея и уравнение Гюгонио.

Это соответственно:

$$\left\{{\begin{aligned}u^{2}(v,p)&=u_{0}^{2}+(p-p_{0})(v_{0}+v)\\[1.2ex]e(v,p)&=e_{0}+{\tfrac {1}{2}}(p+p_{0})(v_{0}-v).\end{aligned}}\right.$$

Уравнение Гюгонио в сочетании с фундаментальным уравнением состояния материала:

$$e=e(v,p)$$

описывает в общем случае в плоскости давления-объема кривую, проходящую по условиям (v ₀ , p ₀ ), т. е. кривую Гюгонио , форма которой сильно зависит от типа рассматриваемого материала.

Также принято определять функцию Гюгонио :

$${\mathfrak {h}}(v,s)\equiv e(v,s)-e_{0}+{\tfrac {1}{2}}(p(v,s)+p_{0})(v-v_{0})$$

позволяющий количественно оценить отклонения от уравнения Гюгонио, аналогично предыдущему определению гидравлического напора , что полезно для отклонений от уравнения Бернулли.

Форма конечного объема

С другой стороны, путем интегрирования общего уравнения сохранения:

$${\frac {\partial \mathbf {y} }{\partial t}}+\nabla \cdot \mathbf {F} =\mathbf {s}$$

на фиксированном объеме V _m , а затем на основании теоремы о дивергенции получается:

$${\frac {d}{dt}}\int _{V_{m}}\mathbf {y} dV+\oint _{\partial V_{m}}\mathbf {F} \cdot {\hat {n}}ds=\mathbf {S} .$$

Интегрируя это уравнение также по временному интервалу:

$$\int _{V_{m}}\mathbf {y} (\mathbf {r} ,t_{n+1})\,dV-\int _{V_{m}}\mathbf {y} (\mathbf {r} ,t_{n})\,dV+\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\mathbf {F} \cdot {\hat {n}}\,ds\,dt=\mathbf {0} .$$

Теперь, определив сохраняемую величину узла:

$$\mathbf {y} _{m,n}\equiv {\frac {1}{V_{m}}}\int _{V_{m}}\mathbf {y} (\mathbf {r} ,t_{n})\,dV,$$

выводим форму конечного объема:

$$\mathbf {y} _{m,n+1}=\mathbf {y} _{m,n}-{\frac {1}{V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\mathbf {F} \cdot {\hat {n}}\,ds\,dt.$$

В частности, для уравнений Эйлера после определения сохраняющихся величин конвективные переменные выводятся путем обратной замены:

$${\begin{cases}\displaystyle \mathbf {u} _{m,n}={\frac {\mathbf {j} _{m,n}}{\rho _{m,n}}}\\[1.2ex]\displaystyle e_{m,n}={\frac {E_{m,n}^{t}}{\rho _{m,n}}}-{\frac {1}{2}}u_{m,n}^{2}.\end{cases}}$$

Тогда явные выражения исходных конвективных переменных в конечном объеме будут следующими:

Уравнения Эйлера
( Форма конечного объема )

$\left\{{\begin{aligned}\rho _{m,n+1}&=\rho _{m,n}-{\frac {1}{V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\rho \mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {u} _{m,n+1}&=\mathbf {u} _{m,n}-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}(\rho \mathbf {u} \otimes \mathbf {u} -p\mathbf {I} )\cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {e} _{m,n+1}&=\mathbf {e} _{m,n}-{\frac {1}{2}}\left(u_{m,n+1}^{2}-u_{m,n}^{2}\right)-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\left(\rho e+{\frac {1}{2}}\rho u^{2}+p\right)\mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\end{aligned}}\right..$

Ограничения

Показано, что уравнения Эйлера не являются полной системой уравнений, но для принятия единственного решения требуют некоторых дополнительных ограничений: это уравнение состояния рассматриваемого материала. Чтобы быть совместимыми с термодинамикой, эти уравнения состояния должны удовлетворять двум законам термодинамики. С другой стороны, неравновесные системы по определению описываются законами, лежащими вне этих законов. Ниже мы перечислим некоторые очень простые уравнения состояния и соответствующее влияние на уравнения Эйлера.

Идеальный политропный газ

Смотрите также: идеальный газ

Для идеального политропного газа основное уравнение состояния имеет вид:

$$e(v,s)=e_{0}e^{(\gamma -1)m\left(s-s_{0}\right)}\left({v_{0} \over v}\right)^{\gamma -1}$$

где $e$ это удельная энергия, $v$ это удельный объем, $s$ это удельная энтропия, $m$ молекулярная масса, $\gamma$ здесь считается константой ( политропный процесс ), и можно показать, что она соответствует коэффициенту теплоемкости . Можно показать, что это уравнение согласуется с обычными уравнениями состояния, используемыми в термодинамике.

показывать

Демонстрация соответствия термодинамике идеального газа.

By the thermodynamic definition of temperature:

$$T(e)\equiv {\partial e \over \partial s}=(\gamma -1)me$$

Where the temperature is measured in energy units. At first, note that by combining these two equations one can deduce the ideal gas law:

$$pv=mT$$

or, in the usual form:

$$p=nT$$

where: $n\equiv {\frac {m}{v}}$ is the number density of the material. On the other hand the ideal gas law is less strict than the original fundamental equation of state considered.

Now consider the molar heat capacity associated to a process x:

$$c_{x}=\left(mT{\partial s \over \partial T}\right)_{x}$$

according to the first law of thermodynamics:

$$de(v,s)=-pdv+T\,ds$$

it can be simply expressed as:

$$c_{x}\equiv m\left({\partial e \over \partial T}\right)_{x}+mp\left({\partial v \over \partial T}\right)_{x}$$

Now inverting the equation for temperature T(e) we deduce that for an ideal polytropic gas the isochoric heat capacity is a constant:

$$c_{v}\equiv m\left({\partial e \over \partial T}\right)_{v}=m{de \over dT}={\frac {1}{(\gamma -1)}}$$

and similarly for an ideal polytropic gas the isobaric heat capacity results constant:

$$c_{p}\equiv m\left({\partial e \over \partial T}\right)_{p}+mp\left({\partial v \over \partial T}\right)_{p}=m{de \over dT}+p\left({\partial v \over \partial T}\right)_{p}={\frac {1}{(\gamma -1)}}+1$$

This brings to two important relations between heat capacities: the constant gamma actually represents the heat capacity ratio in the ideal polytropic gas:

$${\frac {c_{p}}{c_{v}}}=\gamma$$

and one also arrives to the Meyer's relation:

$$c_{p}=c_{v}+1$$

The specific energy is then, by inverting the relation T(e):

$$e(T)={\frac {mT}{\gamma -1}}=c_{v}mT$$

The specific enthalpy results by substitution of the latter and of the ideal gas law:

$$h(T)\equiv e(T)+(pv)(T)=c_{v}mT+mT=c_{p}mT$$

Из этого уравнения можно вывести уравнение давления по его термодинамическому определению:

$$p(v,e)\equiv -{\partial e \over \partial v}=(\gamma -1){\frac {e}{v}}$$

Инвертируя его, приходим к механическому уравнению состояния:

$$e(v,p)={\frac {pv}{\gamma -1}}$$

Тогда для идеального газа уравнения Эйлера для сжимаемости можно просто выразить в механических или примитивных переменных (удельном объеме, скорости потока и давлении), взяв набор уравнений термодинамической системы и изменив уравнение энергии в уравнение давления с помощью этого механического уравнения. уравнение состояния. Наконец, в конвективной форме они приводят:

Уравнения Эйлера для идеального политропного газа
( конвективная форма )

$\left\{{\begin{aligned}{Dv \over Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=v\nabla p+\mathbf {g} \\[1.2ex]{Dp \over Dt}&=-\gamma p\nabla \cdot \mathbf {u} \end{aligned}}\right.$

и в одномерной квазилинейной форме получают:

$${\frac {\partial \mathbf {y} }{\partial t}}+\mathbf {A} {\frac {\partial \mathbf {y} }{\partial x}}={\mathbf {0} }.$$

где консервативная векторная переменная равна:

$${\mathbf {y} }={\begin{pmatrix}v\\u\\p\end{pmatrix}}$$

и соответствующая матрица Якобиана:

$${\mathbf {A} }={\begin{pmatrix}u&-v&0\\0&u&v\\0&\gamma p&u\end{pmatrix}}.$$

Устойчивый поток в координатах материала

удобно выбрать систему Френе–Серре вдоль линии тока В случае установившегося течения в качестве системы координат для описания уравнения Эйлера установившегося импульса :

$${\boldsymbol {u}}\cdot \nabla {\boldsymbol {u}}=-{\frac {1}{\rho }}\nabla p,$$

где $\mathbf {u}$, $p$ и $\rho$ обозначают скорость потока , давление и плотность соответственно.

Позволять $\left\{\mathbf {e} _{s},\mathbf {e} _{n},\mathbf {e} _{b}\right\}$ Френе–Серре — ортонормированный базис , который состоит из касательного единичного вектора, нормального единичного вектора и бинормального единичного вектора к линии тока соответственно. Поскольку линия тока представляет собой кривую, касательную к вектору скорости потока, левую часть приведенного выше уравнения, конвективную производную скорости, можно описать следующим образом:

$${\begin{aligned}{\boldsymbol {u}}\cdot \nabla {\boldsymbol {u}}\\[1ex]&=u{\frac {\partial }{\partial s}}(u{\boldsymbol {e}}_{s})&({\boldsymbol {u}}=u{\boldsymbol {e}}_{s},~{\partial /\partial s}\equiv {\boldsymbol {e}}_{s}\cdot \nabla )\\[1ex]&=u{\frac {\partial u}{\partial s}}{\boldsymbol {e}}_{s}+{\frac {u^{2}}{R}}{\boldsymbol {e}}_{n}&(\because ~{\frac {\partial {\boldsymbol {e}}_{s}}{\partial s}}={\frac {1}{R}}{\boldsymbol {e}}_{n}),\end{aligned}}$$

где $R$ – радиус кривизны линии тока.

Таким образом, импульсная часть уравнений Эйлера для установившегося течения имеет простой вид:

$${\begin{cases}\displaystyle u{\frac {\partial u}{\partial s}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial s}},\\\displaystyle {u^{2} \over R}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial n}}&({\partial /\partial n}\equiv {\boldsymbol {e}}_{n}\cdot \nabla ),\\\displaystyle 0=-{\frac {1}{\rho }}{\frac {\partial p}{\partial b}}&({\partial /\partial b}\equiv {\boldsymbol {e}}_{b}\cdot \nabla ).\end{cases}}$$

Для баротропного потока $(\rho =\rho (p))$, уравнение Бернулли выводится из первого уравнения:

$${\frac {\partial }{\partial s}}\left({\frac {u^{2}}{2}}+\int {\frac {\mathrm {d} p}{\rho }}\right)=0.$$

Второе уравнение выражает, что в случае, если линия тока искривлена, должен существовать градиент давления, нормальный к линии тока, поскольку центростремительное ускорение пакета жидкости создается только нормальным градиентом давления.

Третье уравнение выражает, что давление постоянно вдоль бинормальной оси.

Теорема о кривизне линий

«Теорема кривизны обтекаемой линии» утверждает, что давление на верхней поверхности профиля ниже, чем давление на большом расстоянии, и что давление на нижней поверхности выше, чем давление на большом расстоянии; следовательно, разница давлений между верхней и нижней поверхностями аэродинамического профиля создает подъемную силу.

Позволять $r$ — расстояние от центра кривизны линии тока, тогда второе уравнение записывается следующим образом:

$${\frac {\partial p}{\partial r}}=\rho {\frac {u^{2}}{r}}~(>0),$$

где ${\partial /\partial r}=-{\partial /\partial n}.$

Это уравнение гласит:

При установившемся течении невязкой жидкости без внешних сил центр кривизны линии тока лежит в сторону уменьшения радиального давления.

Хотя эта связь между полем давления и кривизной потока очень полезна, она не имеет названия в англоязычной научной литературе. Японские гидродинамики называют эту взаимосвязь «теоремой кривизны линии потока».

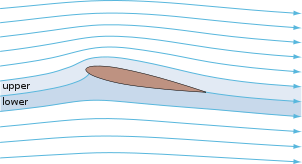
такое низкое давление Эта «теорема» ясно объясняет, почему в центре вихрей . которые состоят из концентрических кругов линий тока.Это также способ интуитивно объяснить, почему аэродинамические профили создают подъемную силу .

Точные решения

Все решения потенциального потока также являются решениями уравнений Эйлера, в частности уравнений Эйлера несжимаемой жидкости, когда потенциал гармоничен.

Двумерный параллельный сдвиговый поток.

Решениями уравнений Эйлера с завихренностью являются:

• параллельные сдвиговые потоки - когда поток однонаправленный, а скорость потока меняется только в направлениях поперечного потока, например, в декартовой системе координат. $(x,y,z)$ поток находится, например, в $x$-направление – единственная ненулевая составляющая скорости $u_{x}(y,z)$ зависит только от $y$ и $z$ и не на $x.$
• Поток Арнольда–Бельтрами–Чилдресса – точное решение уравнений Эйлера несжимаемой жидкости.
• Два решения трехмерных уравнений Эйлера с цилиндрической симметрией были представлены Гиббоном, Муром и Стюартом в 2003 году. Эти два решения имеют бесконечную энергию; они взрываются повсюду в пространстве за конечное время.

См. также

• Теорема Бернулли
• Теорема Кельвина о циркуляции
• Уравнения Коши
• Число Фруда
• Уравнения Маделунга
• Уравнения Навье – Стокса.
• Уравнение Бюргерса
• Уравнения джинсов
• Идеальная жидкость

Ссылки

Источники

• Андерсон, Джон (1995). Вычислительная гидродинамика . Макгроу-Хилл Образование. ISBN  978-0-07-001685-9 .
• Бабинский, Хольгер (ноябрь 2003 г.), «Как работают крылья?» (PDF) , Физическое образование , 38 (6): 497–503, Бибкод : 2003PhyEd..38..497B , doi : 10.1088/0031-9120/38/6/001 , S2CID   1657792
• Хорин, Александр Ж.; Марсден, Джеррольд Э. (2013). Математическое введение в механику жидкости . Спрингер. ISBN  978-1-4612-0883-9 .
• Христодулу, Деметриос (октябрь 2007 г.). «Уравнения Эйлера течения сжимаемой жидкости» (PDF) . Бюллетень Американского математического общества . 44 (4): 581–602. дои : 10.1090/S0273-0979-07-01181-0 .
• Эйлер, Леонард (1757). « Общие принципы движения жидкостей». Мемуары Берлинской академии наук (на французском языке). 11 : 274–315.
• Фэй, Джеймс А. (1994). Введение в механику жидкости . МТИ Пресс. ISBN  978-0-262-06165-0 .
• Фридлендер, С.; Серр, Д., ред. (2003). Справочник по математической гидродинамике – Том 2 . Эльзевир. ISBN  978-0-444-51287-1 .
• Friedmann, A. (1934) [1922]. Kochin, Nikolai (ed.). Опыт гидромеханики сжимаемой жидкости [ An essay on hydrodynamics of compressible fluid ] (in Russian). Petrograd . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Гиббон, доктор медицинских наук; Мур, доктор медицинских наук; Стюарт, Дж. Т. (2003). «Точные решения с бесконечной энергией и разрушением трехмерных уравнений Эйлера». Нелинейность . 16 (5): 1823–1831. Бибкод : 2003Nonli..16.1823G . дои : 10.1088/0951-7715/16/5/315 . S2CID   250797052 .
• Хендерсон, LF (2000). «Общие законы распространения ударных волн в материи» . В Бен-Доре, Габи; Игра, Озер; Эльперин, Тов (ред.). Справочник по ударным волнам, набор из трех томов . Эльзевир. ISBN  978-0-08-053372-8 .
• Хантер, Джон К. (25 сентября 2006 г.), Введение в уравнения Эйлера для несжимаемой жидкости (PDF) , получено 31 мая 2019 г.
• Исао Имаи (IMAI, Исао) (ноябрь 1973 г.) «Динамика жидкости (Часть 1)» [ Динамика жидкости 1 ). ] (на японском языке ISBN  4-7853-2314-0 .
• Ландау, Л.Д.; Лифшиц, Э.М. (2013). Механика жидкости . Эльзевир. ISBN  978-1-4831-4050-6 .
• Маркьоро, К.; Пульвиренти, М. (1994). Математическая теория несжимаемых невязких жидкостей . Прикладные математические науки. Том. 96. Нью-Йорк: Спрингер. ISBN  0-387-94044-8 .
• Квартапель, Луиджи; Аутери, Франко (2013). Динамика сжимаемой жидкости [ Динамика сжимаемой жидкости ] (на итальянском языке). СЕА. ISBN  978-88-08-18558-7 .
• Торо, EF (1999). Решатели Римана и численные методы гидродинамики: практическое введение . Спрингер. ISBN  978-3-540-65966-2 .
• Валорани, Мауро; Насути, Франческо (nd), Методы анализа турбомашин (PDF) , Sapienza - Universit`a di Roma, заархивировано из оригинала (PDF) 16 мая 2022 г. , получено 31 мая 2019 г.
• Зингале, М. (16 апреля 2013 г.), Заметки об уравнениях Эйлера (PDF) , заархивировано из оригинала (PDF) 19 июня 2015 г. , получено 31 мая 2019 г.

Дальнейшее чтение

• Бадин, Г.; Кришиани, Ф. (2018). Вариационная формулировка жидкости и геофизическая гидродинамика - Механика, симметрия и законы сохранения - . Спрингер. п. 218. Бибкод : 2018vffg.book.....B . дои : 10.1007/978-3-319-59695-2 . ISBN  978-3-319-59694-5 . S2CID   125902566 .
• Бэтчелор, ГК (1967). Введение в гидродинамику . Издательство Кембриджского университета. ISBN  0-521-66396-2 .
• Томпсон, Филип А. (1972). Поток сжимаемой жидкости . Нью-Йорк: МакГроу-Хилл. ISBN  0-07-064405-5 .