метод Эйлера

Для интегрирования по характеристике Эйлера см. Исчисление Эйлера . Чтобы узнать о методе Эйлера для факторизации целого числа, см. Метод факторизации Эйлера .

(Рисунок 1) Иллюстрация метода Эйлера. Неизвестная кривая выделена синим цветом, а ее полигональная аппроксимация — красным.

В математике и информатике ( метод Эйлера также называемый прямым методом Эйлера процедура первого порядка ) — это численная для решения обыкновенных дифференциальных уравнений (ОДУ) с заданным начальным значением . Это самый простой явный метод численного интегрирования обыкновенных дифференциальных уравнений и самый простой метод Рунге – Кутты . Метод Эйлера назван в честь Леонарда Эйлера , который впервые предложил его в своей книге Institutionum Calculi Integralis (опубликованной в 1768–1770 гг.).

Метод Эйлера является методом первого порядка, что означает, что локальная ошибка (ошибка на шаг) пропорциональна квадрату размера шага, а глобальная ошибка (ошибка в данный момент времени) пропорциональна размеру шага. Метод Эйлера часто служит основой для построения более сложных методов, например метода предиктора-корректора .

Геометрическое описание

Цель и почему это работает

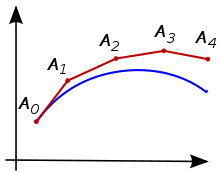
Рассмотрим задачу вычисления формы неизвестной кривой, начинающейся в заданной точке и удовлетворяющей заданному дифференциальному уравнению. Здесь дифференциальное уравнение можно рассматривать как формулу, по которой к кривой наклон касательной можно вычислить в любой точке кривой после расчета положения этой точки.

Идея состоит в том, что, хотя кривая изначально неизвестна, ее начальная точка, которую мы обозначаем через $A_{0},$известно (см. рисунок 1). Тогда из дифференциального уравнения наклон кривой при $A_{0}$ можно вычислить и так касательную.

Сделайте небольшой шаг по касательной до точки $A_{1}.$ На этом небольшом шаге наклон не слишком сильно меняется, поэтому $A_{1}$будет близко к кривой. Если мы притворимся, что $A_{1}$ все еще находится на кривой, те же рассуждения, что и для точки $A_{0}$выше можно использовать. После нескольких шагов ломаная кривая ( $A_{0}A_{1}A_{2}A_{3}\dots$) вычисляется. В общем, эта кривая не отличается слишком далеко от исходной неизвестной кривой, и ошибку между двумя кривыми можно сделать небольшой, если размер шага достаточно мал и интервал вычислений конечен.

Процесс первого порядка

Если заданы значения для $t_{0}$ и $y(t_{0})$и производная от $y$ является заданной функцией $t$ и $y$ обозначается как $y'(t)=f{\bigl (}t,y(t){\bigr )}$. Начните процесс с установки $y_{0}=y(t_{0})$. Далее выберите значение $h$ для размера каждого шага по оси t и установите $t_{n}=t_{0}+nh$ (или эквивалентно $t_{n+1}=t_{n}+h$). Теперь метод Эйлера используется для нахождения $y_{n+1}$ от $y_{n}$ и $t_{n}$:

$y_{n+1}=y_{n}+hf(t_{n},y_{n}).$

Значение $y_{n}$ является приближением решения в момент времени $t_{n}$, то есть, $y_{n}\approx y(t_{n})$. Метод Эйлера является явным , т.е. решение $y_{n+1}$ является явной функцией $y_{i}$ для $i\leq n$.

Процесс высшего порядка

Хотя метод Эйлера объединяет ОДУ первого порядка, любое ОДУ порядка $N$можно представить как систему ОДУ первого порядка. Когда дана ОДА порядка $N$ определяется как

$y^{(N+1)}(t)=f\left(t,y(t),y'(t),\ldots ,y^{(N)}(t)\right),$

а также $h$, $t_{0}$, и $y_{0},y'_{0},\dots ,y_{0}^{(N)}$, мы реализуем следующую формулу, пока не достигнем аппроксимации решения ОДУ в желаемый момент времени:

${\vec {y}}_{i+1}={\begin{pmatrix}y_{i+1}\\y'_{i+1}\\\vdots \\y_{i+1}^{(N-1)}\\y_{i+1}^{(N)}\end{pmatrix}}={\begin{pmatrix}y_{i}+h\cdot y'_{i}\\y'_{i}+h\cdot y''_{i}\\\vdots \\y_{i}^{(N-1)}+h\cdot y_{i}^{(N)}\\y_{i}^{(N)}+h\cdot f\left(t_{i},y_{i},y'_{i},\ldots ,y_{i}^{(N)}\right)\end{pmatrix}}$

С этими системами первого порядка можно обращаться методом Эйлера или, фактически, любой другой схемой для систем первого порядка.

Пример первого порядка

Учитывая проблему начального значения

$y'=y,\quad y(0)=1,$

мы хотели бы использовать метод Эйлера для аппроксимации $y(4)$.

Использование размера шага, равного 1 ( h = 1 )

(Рисунок 2) Иллюстрация численного интегрирования уравнения $y'=y,y(0)=1.$Синий — метод Эйлера; зеленый — метод средней точки ; красный, точное решение, $y=e^{t}.$ Размер шага $h=1.0.$

Метод Эйлера

$y_{n+1}=y_{n}+hf(t_{n},y_{n}).$

поэтому сначала мы должны вычислить $f(t_{0},y_{0})$. В этом простом дифференциальном уравнении функция $f$ определяется $f(t,y)=y$. У нас есть

$f(t_{0},y_{0})=f(0,1)=1.$

Выполнив описанный выше шаг, мы нашли наклон линии, касательной к кривой решения в точке $(0,1)$. Напомним, что наклон определяется как изменение $y$ разделенное на изменение $t$, или ${\textstyle {\frac {\Delta y}{\Delta t}}}$.

Следующий шаг — умножить указанное выше значение на размер шага. $h$, который здесь мы принимаем равным единице:

$h\cdot f(y_{0})=1\cdot 1=1.$

Поскольку размер шага — это изменение $t$, когда мы умножаем размер шага и наклон касательной, мы получаем изменение $y$ценить. Это значение затем добавляется к исходному $y$ value для получения следующего значения, которое будет использоваться для вычислений.

$y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.$

Вышеуказанные шаги следует повторить, чтобы найти $y_{2}$, $y_{3}$ и $y_{4}$.

${\begin{aligned}y_{2}&=y_{1}+hf(y_{1})=2+1\cdot 2=4,\\y_{3}&=y_{2}+hf(y_{2})=4+1\cdot 4=8,\\y_{4}&=y_{3}+hf(y_{3})=8+1\cdot 8=16.\end{aligned}}$

Из-за повторяющегося характера этого алгоритма может быть полезно организовать вычисления в виде диаграммы, как показано ниже, чтобы избежать ошибок.

$n$	$y_{n}$	$t_{n}$	$f(t_{n},y_{n})$	$h$	$\Delta y$	$y_{n+1}$
0	1	0	1	1	1	2
1	2	1	2	1	2	4
2	4	2	4	1	4	8
3	8	3	8	1	8	16

Вывод этого вычисления таков: $y_{4}=16$. Точное решение дифференциального уравнения есть $y(t)=e^{t}$, так $y(4)=e^{4}\approx 54.598$. Хотя аппроксимация метода Эйлера в данном конкретном случае была не очень точной, в частности из-за большого размера шага. $h$, его поведение качественно правильное, как показано на рисунке.

Использование других размеров шага

(Рисунок 3) Та же иллюстрация для $h=0.25.$

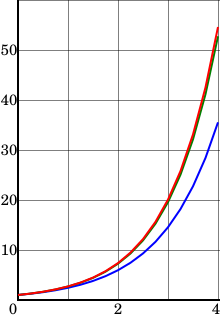
Как было предложено во введении, метод Эйлера более точен, если размер шага $h$меньше. В таблице ниже показаны результаты с разными размерами шага. Верхняя строка соответствует примеру из предыдущего раздела, а вторая строка показана на рисунке.

размер шага	результат метода Эйлера	ошибка
1	16.00	38.60
0.25	35.53	19.07
0.1	45.26	0 9.34
0.05	49.56	0 5.04
0.025	51.98	0 2.62
0.0125	53.26	0 1.34

Ошибка, записанная в последнем столбце таблицы, представляет собой разность точного решения при $t=4$и приближение Эйлера. Внизу таблицы размер шага равен половине размера шага в предыдущей строке, а ошибка также примерно вдвое меньше ошибки в предыдущей строке. Это говорит о том, что ошибка примерно пропорциональна размеру шага, по крайней мере, для достаточно малых значений размера шага. В целом это верно и для других уравнений; см. в разделе «Глобальная ошибка усечения» дополнительные сведения .

Другие методы, такие как метод средней точки , также показанный на рисунках, ведут себя более благоприятно: глобальная ошибка метода средней точки примерно пропорциональна квадрату размера шага. По этой причине метод Эйлера называют методом первого порядка, а метод средней точки — второго порядка.

Из приведенной выше таблицы мы можем экстраполировать, что размер шага, необходимый для получения ответа, правильного до трех знаков после запятой, составляет примерно 0,00001, а это означает, что нам нужно 400 000 шагов. Такое большое количество шагов влечет за собой высокие вычислительные затраты. По этой причине используются методы более высокого порядка, такие как методы Рунге-Кутты или линейные многошаговые методы , особенно если требуется высокая точность.

Пример высшего порядка

Для этого примера третьего порядка предположим, что дана следующая информация:

${\begin{aligned}&y'''+4ty''-t^{2}y'-(\cos {t})y=\sin {t}\\&t_{0}=0\\&y_{0}=y(t_{0})=2\\&y'_{0}=y'(t_{0})=-1\\&y''_{0}=y''(t_{0})=3\\&h=0.5\end{aligned}}$

Отсюда мы можем выделить y''', чтобы получить уравнение:

$f\left(t,y,y',y''\right)=y'''=\sin {t}+(\cos {t})y+t^{2}y'-4ty''$

Используя это, мы можем получить решение для ${\vec {y}}_{1}$:

$${\vec {y}}_{1}={\begin{pmatrix}y_{1}\\y_{1}'\\y_{1}''\end{pmatrix}}={\begin{pmatrix}y_{0}+h\cdot y'_{0}\\y'_{0}+h\cdot y''_{0}\\y''_{0}+h\cdot f\left(t_{0},y_{0},y'_{0},y''_{0}\right)\end{pmatrix}}={\begin{pmatrix}2+0.5\cdot -1\\-1+0.5\cdot 3\\3+0.5\cdot \left(\sin {0}+(\cos {0})\cdot 2+0^{2}\cdot (-1)-4\cdot 0\cdot 3\right)\end{pmatrix}}={\begin{pmatrix}1.5\\0.5\\4\end{pmatrix}}$$

И используя решение для ${\vec {y}}_{1}$, мы можем получить решение для ${\vec {y}}_{2}$:

$${\vec {y}}_{2}={\begin{pmatrix}y_{2}\\y_{2}'\\y_{2}''\end{pmatrix}}={\begin{pmatrix}y_{1}+h\cdot y'_{1}\\y'_{1}+h\cdot y''_{1}\\y''_{1}+h\cdot f\left(t_{1},y_{1},y'_{1},y''_{1}\right)\end{pmatrix}}={\begin{pmatrix}1.5+0.5\cdot 0.5\\0.5+0.5\cdot 4\\2+0.5\cdot \left(\sin {0.5}+(\cos {0.5})\cdot 1.5+0.5^{2}\cdot 0.5-4\cdot 0.5\cdot 2\right)\end{pmatrix}}={\begin{pmatrix}1.75\\2.5\\0.9604\end{pmatrix}}$$

Мы можем продолжать этот процесс, используя ту же формулу столько, сколько необходимо, чтобы найти любое ${\vec {y}}_{i}$ желанный.

Вывод

Метод Эйлера можно получить несколькими способами.

(1) Во-первых, приведено выше геометрическое описание.

(2) Другая возможность — рассмотреть разложение Тейлора функции $y$ вокруг $t_{0}$:

$y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\tfrac {1}{2}}h^{2}y''(t_{0})+O\left(h^{3}\right).$

Дифференциальное уравнение утверждает, что $y'=f(t,y)$. Если это подставить в разложение Тейлора и игнорировать квадратичные члены и члены более высокого порядка, возникает метод Эйлера.

Расширение Тейлора используется ниже для анализа ошибок, допущенных методом Эйлера, и его можно расширить для получения методов Рунге – Кутты .

(3) Близко связанный вывод заключается в замене прямой конечной разности производной формулой :

$y'(t_{0})\approx {\frac {y(t_{0}+h)-y(t_{0})}{h}}$

в дифференциальном уравнении $y'=f(t,y)$. Опять же, это дает метод Эйлера.

Аналогичные вычисления приводят к методу средней точки и обратному методу Эйлера .

(4) Наконец, можно проинтегрировать дифференциальное уравнение из $t_{0}$ к $t_{0}+h$ и примените фундаментальную теорему исчисления, чтобы получить:

$y(t_{0}+h)-y(t_{0})=\int _{t_{0}}^{t_{0}+h}f{\bigl (}t,y(t){\bigr )}\,\mathrm {d} t.$

Теперь аппроксимируем интеграл методом левого прямоугольника (только с одним прямоугольником):

$\int _{t_{0}}^{t_{0}+h}f{\bigl (}t,y(t){\bigr )}\,\mathrm {d} t\approx hf{\bigl (}t_{0},y(t_{0}){\bigr )}.$

Объединив оба уравнения, мы снова получаем метод Эйлера.

Эту линию мысли можно продолжить, придя к различным линейным многошаговым методам .

Локальная ошибка усечения

Локальная ошибка усечения метода Эйлера — это ошибка, допущенная за один шаг. Это разница между численным решением после одного шага, $y_{1}$, и точное решение в момент времени $t_{1}=t_{0}+h$. Численное решение имеет вид

$y_{1}=y_{0}+hf(t_{0},y_{0}).$

Для точного решения мы используем разложение Тейлора, упомянутое в разделе «Вывод» выше:

$y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\tfrac {1}{2}}h^{2}y''(t_{0})+O\left(h^{3}\right).$

Локальная ошибка усечения (LTE), вносимая методом Эйлера, определяется разницей между этими уравнениями:

$\mathrm {LTE} =y(t_{0}+h)-y_{1}={\tfrac {1}{2}}h^{2}y''(t_{0})+O\left(h^{3}\right).$

Этот результат справедлив, если $y$ имеет ограниченную третью производную.

Это показывает, что для малых $h$, локальная ошибка усечения примерно пропорциональна $h^{2}$. Это делает метод Эйлера менее точным, чем методы более высокого порядка, такие как методы Рунге-Кутты и линейные многошаговые методы , для которых локальная ошибка усечения пропорциональна более высокой степени размера шага.

Немного другую формулировку для локальной ошибки усечения можно получить, используя форму Лагранжа для остаточного члена в теореме Тейлора . Если $y$ имеет непрерывную вторую производную, то существует $\xi \in [t_{0},t_{0}+h]$ такой, что

$\mathrm {LTE} =y(t_{0}+h)-y_{1}={\tfrac {1}{2}}h^{2}y''(\xi ).$

В приведенных выше выражениях для ошибки вторая производная неизвестного точного решения $y$можно заменить выражением, включающим правую часть дифференциального уравнения. Действительно, это следует из уравнения $y'=f(t,y)$ что

$y''(t_{0})={\frac {\partial f}{\partial t}}{\bigl (}t_{0},y(t_{0}){\bigr )}+{\frac {\partial f}{\partial y}}{\bigl (}t_{0},y(t_{0}){\bigr )}\,f{\bigl (}t_{0},y(t_{0}){\bigr )}.$

Глобальная ошибка усечения

Глобальная ошибка усечения — это ошибка в фиксированный момент времени. $t_{i}$, после любого количества шагов, которые метод должен выполнить, чтобы достичь этого времени с начального момента. Глобальная ошибка усечения — это совокупный эффект локальных ошибок усечения, совершенных на каждом этапе. Число шагов легко определить как ${\textstyle {\frac {t_{i}-t_{0}}{h}}}$, что пропорционально ${\textstyle {\frac {1}{h}}}$, а ошибка, совершаемая на каждом шаге, пропорциональна $h^{2}$(см. предыдущий раздел). Таким образом, следует ожидать, что глобальная ошибка усечения будет пропорциональна $h$.

Это интуитивное рассуждение можно уточнить. Если решение $y$ имеет ограниченную вторую производную и $f$ является липшицевым непрерывным по своему второму аргументу, то глобальная ошибка усечения (обозначается как $|y(t_{i})-y_{i}|$) ограничено

$|y(t_{i})-y_{i}|\leq {\frac {hM}{2L}}\left(e^{L(t_{i}-t_{0})}-1\right)$

где $M$ является верхней границей второй производной $y$ на заданном интервале и $L$ константа Липшица $f$. Или проще говоря, когда $y'(t)=f(t,y)$, Значение ${\textstyle L={\text{max}}{\bigl (}|{\frac {d}{dy}}{\bigl [}f(t,y){\bigr ]}|{\bigr )}}$ (такой, что $t$считается константой). В отличие, ${\textstyle M={\text{max}}{\bigl (}|{\frac {d^{2}}{dt^{2}}}{\bigl [}y(t){\bigr ]}|{\bigr )}}$ где функция $y(t)$ является точным решением, содержащим только $t$ переменная.

Точная форма этой оценки не имеет практического значения, поскольку в большинстве случаев она значительно переоценивает реальную ошибку, допущенную методом Эйлера. Важно то, что он показывает, что глобальная ошибка усечения (приблизительно) пропорциональна $h$. По этой причине метод Эйлера называют методом первого порядка.

Пример

Если у нас есть дифференциальное уравнение $y'=1+(t-y)^{2}$, и точное решение $y=t+{\frac {1}{t-1}}$, и мы хотим найти $M$ и $L$ когда $2\leq t\leq 3$.

$$L={\text{max}}{\bigl (}|{\frac {d}{dy}}{\bigl [}f(t,y){\bigr ]}|{\bigr )}=\max _{2\leq t\leq 3}{\bigl (}|{\frac {d}{dy}}{\bigl [}1+(t-y)^{2}{\bigr ]}|{\bigr )}=\max _{2\leq t\leq 3}{\bigl (}|2(t-y)|{\bigr )}=\max _{2\leq t\leq 3}{\bigl (}|2(t-[t+{\frac {1}{t-1}}])|{\bigr )}=\max _{2\leq t\leq 3}{\bigl (}|-{\frac {2}{t-1}}|{\bigr )}=2$$

$$M={\text{max}}{\bigl (}|{\frac {d^{2}}{dt^{2}}}{\bigl [}y(t){\bigr ]}|{\bigr )}=\max _{2\leq t\leq 3}\left(|{\frac {d^{2}}{dt^{2}}}{\bigl [}t+{\frac {1}{1-t}}{\bigr ]}|\right)=\max _{2\leq t\leq 3}\left(|{\frac {2}{(-t+1)^{3}}}|\right)=2$$

Таким образом, мы можем найти границу ошибки при t=2,5 и h=0,5:

$${\text{error bound}}={\frac {hM}{2L}}\left(e^{L(t_{i}-t_{0})}-1\right)={\frac {0.5\cdot 2}{2\cdot 2}}\left(e^{2(2.5-2)}-1\right)=0.42957$$

Обратите внимание, что t ₀ равно 2, поскольку это нижняя граница t в $2\leq t\leq 3$.

Численная стабильность

(Рисунок 4) Решение $y'=-2.3y$ вычисляется методом Эйлера с размером шага $h=1$ (синие квадраты) и $h=0.7$(красные кружки). Черная кривая показывает точное решение.

Метод Эйлера также может быть численно нестабильным , особенно для жестких уравнений , а это означает, что численное решение становится очень большим для уравнений, для которых нет точного решения. Это можно проиллюстрировать с помощью линейного уравнения

$y'=-2.3y,\qquad y(0)=1.$

Точное решение $y(t)=e^{-2.3t}$, который убывает до нуля при $t\to \infty$. Однако если к этому уравнению применить метод Эйлера с размером шага $h=1$, то численное решение качественно неверно: оно колеблется и растет (см. рисунок). Вот что значит быть нестабильным. Если используется меньший размер шага, например $h=0.7$, то численное решение затухает до нуля.

(Рисунок 5) Розовым диском показана область устойчивости метода Эйлера.

Если применить метод Эйлера к линейному уравнению $y'=ky$, то численное решение неустойчиво, если произведение $hk$ находится за пределами региона

${\bigl \{}z\in \mathbf {C} \,{\big |}\,|z+1|\leq 1{\bigr \}},$

показано справа. Эта область называется областью (линейной) устойчивости . В примере $k=-2.3$, так что если $h=1$ затем $hk=-2.3$ которая находится вне области устойчивости, и, следовательно, численное решение неустойчиво.

Это ограничение, а также медленная сходимость ошибки с $h$ — означает, что метод Эйлера используется нечасто, за исключением простого примера численного интегрирования. . Часто модели физических систем содержат члены, представляющие быстро распадающиеся элементы (т.е. с большими отрицательными экспоненциальными аргументами). Даже если они не представляют интереса для общего решения, нестабильность, которую они могут вызвать, означает, что при использовании метода Эйлера потребуется исключительно малый временной шаг.

Ошибки округления

В ногу $n$ В методе Эйлера ошибка округления примерно равна величине $\varepsilon y_{n}$ где $\varepsilon$это машина эпсилон . Предполагая, что ошибки округления являются независимыми случайными величинами, ожидаемая общая ошибка округления пропорциональна ${\textstyle {\frac {\varepsilon }{\sqrt {h}}}}$. Таким образом, для чрезвычайно малых значений размера шага ошибка усечения будет небольшой, но влияние ошибки округления может быть большим. Большую часть эффекта ошибки округления можно легко избежать, если компенсированное суммирование . в формуле метода Эйлера использовать

Модификации и расширения

Простой модификацией метода Эйлера, которая устраняет отмеченные выше проблемы устойчивости, является обратный метод Эйлера :

$y_{n+1}=y_{n}+hf(t_{n+1},y_{n+1}).$

Он отличается от (стандартного или прямого) метода Эйлера тем, что функция $f$оценивается в конечной точке шага, а не в начальной точке. Обратный метод Эйлера является неявным методом . Это означает, что формула обратного метода Эйлера имеет $y_{n+1}$с обеих сторон, поэтому при применении обратного метода Эйлера нам приходится решать уравнение. Это делает внедрение более дорогостоящим.

Другие модификации метода Эйлера, которые помогают обеспечить стабильность, дают экспоненциальный метод Эйлера или полунеявный метод Эйлера .

Более сложные методы позволяют достичь более высокого порядка (и большей точности). Одна из возможностей — использовать больше оценок функций. Это иллюстрируется методом средней точки , который уже упоминался в этой статье:

$y_{n+1}=y_{n}+hf\left(t_{n}+{\tfrac {1}{2}}h,y_{n}+{\tfrac {1}{2}}hf(t_{n},y_{n})\right)$.

Это приводит к семейству методов Рунге-Кутты .

Другая возможность — использовать больше прошлых значений, как показано двухэтапным методом Адамса-Башфорта:

$y_{n+1}=y_{n}+{\tfrac {3}{2}}hf(t_{n},y_{n})-{\tfrac {1}{2}}hf(t_{n-1},y_{n-1}).$

Это приводит к семейству линейных многошаговых методов . Существуют и другие модификации, в которых используются методы измерения сжатия для минимизации использования памяти.

В популярной культуре

В фильме «Скрытые фигуры» Кэтрин Гобл прибегает к методу Эйлера при расчете возвращения астронавта Джона Гленна с околоземной орбиты.

См. также

• Метод Кранка – Николсона
• Градиентный спуск аналогично использует конечные шаги, чтобы найти минимумы функций.
• Список методов Рунге-Кутты
• Линейный многошаговый метод
• Численное интегрирование (для вычисления определенных интегралов)
• Численные методы для решения обыкновенных дифференциальных уравнений

Ссылки

• Аткинсон, Кендалл А. (1989). Введение в численный анализ (2-е изд.). Нью-Йорк: Джон Уайли и сыновья . ISBN  978-0-471-50023-0 .
• Ашер, Ури М.; Петцольд, Линда Р. (1998). Компьютерные методы решения обыкновенных дифференциальных уравнений и дифференциально-алгебраических уравнений . Филадельфия: Общество промышленной и прикладной математики . ISBN  978-0-89871-412-8 .
• Мясник, Джон К. (2003). Численные методы решения обыкновенных дифференциальных уравнений . Нью-Йорк: Джон Уайли и сыновья . ISBN  978-0-471-96758-3 .
• Хайрер, Эрнст; Норсетт, Сиверт Пол; Ваннер, Герхард (1993). Решение обыкновенных дифференциальных уравнений I: Нежесткие задачи . Берлин, Нью-Йорк: Springer-Verlag . ISBN  978-3-540-56670-0 .
• Изерлес, Арье (1996). Первый курс численного анализа дифференциальных уравнений . Издательство Кембриджского университета . ISBN  978-0-521-55655-2 .
• Стер, Джозеф; Булирш, Роланд (2002). Введение в численный анализ (3-е изд.). Берлин, Нью-Йорк: Springer-Verlag . ISBN  978-0-387-95452-3 .
• Лакоба, Тарас И. (2012), Простой метод Эйлера и его модификации (PDF) (конспекты лекций для MATH334), Университет Вермонта , получено 29 февраля 2012 г.
• Унни, депутат П. (2017). «Сокращение памяти для численного решения дифференциальных уравнений с использованием компрессионного измерения». 2017 IEEE 13-й Международный коллоквиум по обработке сигналов и ее приложениям (CSPA) . IEEE CSPA . стр. 79–84. дои : 10.1109/CSPA.2017.8064928 . ISBN  978-1-5090-1184-1 . S2CID   13082456 .

Внешние ссылки

• СМИ, связанные с методом Эйлера, на Викискладе?
• Реализации метода Эйлера на разных языках с помощью Rosetta Code
• «Метод Эйлера» , Математическая энциклопедия , EMS Press , 2001 [1994]