Формула обратного дифференцирования

Формула обратного дифференцирования ( BDF ) представляет собой семейство неявных методов численного интегрирования обыкновенных дифференциальных уравнений . Это линейные многошаговые методы , которые для заданной функции и времени аппроксимируют производную этой функции, используя информацию из уже вычисленных моментов времени, тем самым увеличивая точность аппроксимации. Эти методы особенно используются для решения жестких дифференциальных уравнений . Эти методы были впервые представлены Чарльзом Ф. Кертиссом и Джозефом О. Хиршфельдером в 1952 году. В 1967 году эта область была формализована К. Уильямом Гиром в основополагающей статье, основанной на его более ранней неопубликованной работе.

Общая формула

BDF используется для решения проблемы начального значения.

$y'=f(t,y),\quad y(t_{0})=y_{0}.$

Общую формулу BDF можно записать как

$\sum _{k=0}^{s}a_{k}y_{n+k}=h\beta f(t_{n+s},y_{n+s}),$

где $h$ обозначает размер шага и $t_{n}=t_{0}+nh$. С $f$ оценивается для неизвестного $y_{n+s}$, методы BDF неявны и, возможно, требуют решения нелинейных уравнений на каждом шаге. Коэффициенты $a_{k}$ и $\beta$ выбираются так, чтобы метод достиг порядка $s$, что является максимально возможным.

Вывод коэффициентов

Исходя из формулы ${\textstyle y'(t_{n+s})=f(t_{n+s},y(t_{n+s}))}$ один приближается $y(t_{n+s})\approx y_{n+s}$ и $y'(t_{n+s})\approx p_{n,s}'(t_{n+s})$, где $p_{n,s}(t)$ – интерполяционный полином Лагранжа для точек $(t_{n},y_{n}),\ldots ,(t_{n+s},y_{n+s})$. Используя это $t_{n}=t_{0}+nh$ и умножив на $h$ приходим к методу порядка BDF $s$.

Конкретные формулы

-шаговые BDF s с s <7:

• БДФ1: $$y_{n+1}-y_{n}=hf(t_{n+1},y_{n+1})$$ (это обратный метод Эйлера )
• БДФ2: $$y_{n+2}-{\tfrac {4}{3}}y_{n+1}+{\tfrac {1}{3}}y_{n}={\tfrac {2}{3}}hf(t_{n+2},y_{n+2})$$
• БДФ3: $$y_{n+3}-{\tfrac {18}{11}}y_{n+2}+{\tfrac {9}{11}}y_{n+1}-{\tfrac {2}{11}}y_{n}={\tfrac {6}{11}}hf(t_{n+3},y_{n+3})$$
• БДФ4: $$y_{n+4}-{\tfrac {48}{25}}y_{n+3}+{\tfrac {36}{25}}y_{n+2}-{\tfrac {16}{25}}y_{n+1}+{\tfrac {3}{25}}y_{n}={\tfrac {12}{25}}hf(t_{n+4},y_{n+4})$$
• БДФ5: $$y_{n+5}-{\tfrac {300}{137}}y_{n+4}+{\tfrac {300}{137}}y_{n+3}-{\tfrac {200}{137}}y_{n+2}+{\tfrac {75}{137}}y_{n+1}-{\tfrac {12}{137}}y_{n}={\tfrac {60}{137}}hf(t_{n+5},y_{n+5})$$
• БДФ6: $$y_{n+6}-{\tfrac {360}{147}}y_{n+5}+{\tfrac {450}{147}}y_{n+4}-{\tfrac {400}{147}}y_{n+3}+{\tfrac {225}{147}}y_{n+2}-{\tfrac {72}{147}}y_{n+1}+{\tfrac {10}{147}}y_{n}={\tfrac {60}{147}}hf(t_{n+6},y_{n+6})$$

Методы с s > 6 не устойчивы к нулю, поэтому их нельзя использовать.

Стабильность

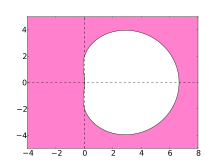
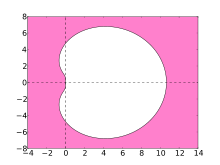
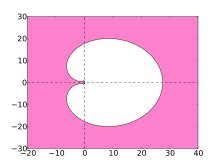
На устойчивость численных методов решения жестких уравнений указывает область их абсолютной устойчивости. Для методов BDF эти области показаны на графиках ниже.

В идеале область содержит левую половину комплексной плоскости, и в этом случае метод называется A-стабильным. Однако линейные многошаговые методы с порядком больше 2 не могут быть A-стабильными . Область устойчивости методов BDF высшего порядка содержит большую часть левой полуплоскости и, в частности, всю отрицательную действительную ось. Методы BDF являются наиболее эффективными линейными многошаговыми методами такого рода.

Розовая область показывает область стабильности методов BDF.

• 
  БДФ1
• 
  БДФ2
• 
  БДФ3
• 
  БДФ4
• 
  БДФ5
• 
  БДФ6

Ссылки

Рекомендованные работы

• Ашер, UM; Петцольд, Л.Р. (1998), Компьютерные методы для обыкновенных дифференциальных уравнений и дифференциально-алгебраических уравнений , SIAM, Филадельфия, ISBN  0-89871-412-5 .
• Изерлес, Арье (1996), Первый курс численного анализа дифференциальных уравнений , Cambridge University Press, ISBN  978-0-521-55655-2 .
• Сюли, Эндре; Майерс, Дэвид (2003), Введение в численный анализ , издательство Кембриджского университета , ISBN  0-521-00794-1 .

Дальнейшее чтение

• Методы BDF на вики SUNDIALS (SUNDIALS — это библиотека, реализующая методы BDF и подобные алгоритмы).