Фазовый портрет

Потенциальная энергия и фазовый портрет простого маятника . Обратите внимание, что ось X, будучи угловой, заворачивается в себя после каждых 2π радиан.

Фазовый портрет затухающего генератора с возрастающей силой затухания. Уравнение движения ${\ddot {x}}+2\gamma {\dot {x}}+\omega ^{2}x=0.$

В математике фазовый портрет — геометрическое представление орбит динамической системы в фазовой плоскости . Каждый набор начальных условий представлен отдельной точкой или кривой .

Фазовые портреты являются бесценным инструментом при изучении динамических систем. Они состоят из графика типичных траекторий в фазовом пространстве . Это раскрывает такую ​​информацию, как наличие аттрактора , отталкивателя или предельного цикла для выбранного значения параметра. Концепция топологической эквивалентности важна для классификации поведения систем, определяя, когда два разных фазовых портрета представляют одно и то же качественное динамическое поведение. Аттрактор — это устойчивая точка, которую еще называют «стоком». Отпугиватель рассматривается как нестабильная точка, которую также называют «источником».

График фазового портрета динамической системы изображает траектории системы (стрелками), а также устойчивые устойчивые состояния (точками) и неустойчивые устойчивые состояния (кружками) в фазовом пространстве. Оси представляют собой переменные состояния .

Примеры

Иллюстрация того, как можно построить фазовый портрет движения простого маятника.

Фазовый портрет уравнения Ван дер Поля , ${\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0$.

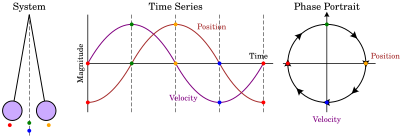
• Простой маятник , см. рисунок (справа).
• Простой гармонический осциллятор , фазовый портрет которого состоит из эллипсов с центром в начале координат, которое является фиксированной точкой.
• Затухающее гармоническое движение , см. анимацию (справа).
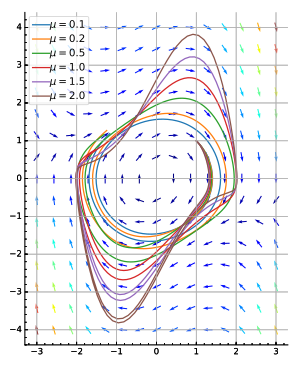
• Осциллятор Ван дер Поля см. рисунок (внизу справа).

поведения обыкновенных

Фазовый портрет представляет собой направленное поведение системы обыкновенных дифференциальных уравнений (ОДУ). Фазовый портрет может указывать на устойчивость системы.

Стабильность

Нестабильный	Большинство решений системы со временем стремятся к ∞.
Асимптотически устойчивый	Все решения системы со временем стремятся к 0.
Нейтрально стабильный	Ни одно из решений системы не стремится со временем к ∞, но большинство решений также не стремятся к 0.

Поведение фазового портрета системы ОДУ может определяться собственными значениями или следом и определителем (след = λ ₁ + λ ₂ , определитель = λ ₁ x λ ₂ ) системы.

Поведение фазового портрета

собственное значение, след, определитель	Форма фазового портрета
λ 1 и λ 2 действительны и имеют противоположный знак; Определитель < 0	Седло (нестабильное)
λ 1 и λ 2 вещественны и одного знака, причем λ 1 ≠ λ 2 ; 0 < определитель < (след 2 / 4)	Узел (стабильный, если трассировка < 0, нестабильный, если трассировка > 0)
λ 1 и λ 2 имеют как действительную, так и мнимую составляющую; (след 2 / 4) < определитель	Спираль (стабильная, если трассировка < 0, нестабильная, если трассировка > 0)

См. также

• Фазовое пространство
• Фазовая плоскость

Ссылки

• Джордан, Д.В.; Смит, П. (2007). Нелинейные обыкновенные дифференциальные уравнения (четвертое изд.). Издательство Оксфордского университета. ISBN  978-0-19-920824-1 . Глава 1.
• Стивен Строгац (2001). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике . ISBN  9780738204536 .

Внешние ссылки

• Линейные фазовые портреты , MIT Mathlet.