Дивергенция

Эта статья о дивергенции в векторном исчислении. О расходимости бесконечных рядов см. Расходящиеся ряды . О расхождениях в статистике см. Дивергенция (статистика) . Чтобы узнать о других значениях, см. Дивергенция (значения) .

Расхождение различных векторных полей. Расхождение векторов из точки ( , y ) равно сумме частной производной по x x x -компоненты и частной производной по -компоненты y , при этом точка: $\nabla \!\cdot (\mathbf {V} (x,y))={\frac {\partial \,{V_{x}(x,y)}}{\partial {x}}}+{\frac {\partial \,{V_{y}(x,y)}}{\partial {y}}}$

В исчислении векторном дивергенция — это векторный оператор , который работает с векторным полем , создавая скалярное поле, дающее количество источника векторного поля в каждой точке. С технической точки зрения, дивергенция представляет собой объемную плотность внешнего потока векторного поля из бесконечно малого объема вокруг данной точки.

В качестве примера рассмотрим воздух, когда он нагревается или охлаждается. Скорость . воздуха в каждой точке определяет векторное поле Пока воздух нагревается в определенной области, он расширяется во всех направлениях, и, таким образом, поле скоростей направлено наружу из этой области. Таким образом, дивергенция поля скорости в этой области будет иметь положительное значение. Пока воздух охлаждается и таким образом сжимается, дивергенция скорости имеет отрицательное значение.

Физическая

С физической точки зрения дивергенция векторного поля — это степень, в которой поток векторного поля ведет себя как источник в данной точке. Это локальная мера его «исходящего» — степени, в которой больше векторов поля выходит из бесконечно малой области пространства, чем входит в нее. Точка выхода потока имеет положительную дивергенцию и часто называется «источником» поля. Точка, в которой поток направлен внутрь, имеет отрицательную расходимость и часто называется «стоком» поля. Чем больше поток поля через небольшую поверхность, окружающую данную точку, тем больше значение расходимости в этой точке. Точка, в которой поток через охватывающую поверхность равен нулю, имеет нулевую расходимость.

Дивергенцию векторного поля часто иллюстрируют на простом примере поля скорости жидкости, жидкости или газа. Движущийся газ имеет скорость , скорость и направление в каждой точке, которые могут быть представлены вектором , поэтому скорость газа образует векторное поле . Если газ нагреть, он расширится. Это вызовет чистое движение частиц газа наружу во всех направлениях. Любая замкнутая поверхность в газе будет окружать газ, который расширяется, поэтому через поверхность будет возникать поток газа наружу. Таким образом, поле скоростей будет везде иметь положительную дивергенцию. Аналогично, если газ охладить, он сожмется. В любом объеме будет больше места для частиц газа, поэтому внешнее давление жидкости вызовет чистый поток объема газа внутрь через любую замкнутую поверхность. Поэтому поле скорости везде имеет отрицательную дивергенцию. Напротив, в газе при постоянной температуре и давлении чистый поток газа из любой замкнутой поверхности равен нулю. Газ может двигаться, но объемная скорость газа, втекающего в любую замкнутую поверхность, должна равняться объемной скорости вытекания, поэтому чистый поток равен нулю. Таким образом, скорость газа всюду имеет нулевую дивергенцию. Поле, всюду имеющее нулевую дивергенцию, называется соленоидальным .

Если газ нагревается только в одной точке или небольшой области или вводится небольшая трубка, которая подает источник дополнительного газа в одну точку, газ там будет расширяться, выталкивая частицы жидкости вокруг себя наружу во всех направлениях. Это создаст направленное наружу поле скоростей по всему газу с центром в нагретой точке. Любая замкнутая поверхность, охватывающая нагретую точку, будет иметь поток частиц газа, выходящий из нее, поэтому в этой точке существует положительная дивергенция. Однако любая замкнутая поверхность, не охватывающая точку, будет иметь постоянную плотность газа внутри, поэтому столько же частиц жидкости входит в объем, сколько покидает его, поэтому чистый поток из объема равен нулю. Поэтому расхождение в любой другой точке равно нулю.

Определение

Дивергенция в точке x есть предел отношения потока $\Phi$ через поверхность S _i (красные стрелки) в объем $|V_{i}|$ для любой последовательности замкнутых областей V ₁ , V ₂ , V ₃ , …, охватывающих x , которая приближается к нулевому объему:
$\operatorname {div} \mathbf {F} =\lim _{|V_{i}|\to 0}{\frac {\Phi (S_{i})}{|V_{i}|}}$

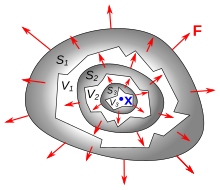
Дивергенция векторного поля F ( x ) в точке x ₀ определяется как предел отношения поверхностного интеграла F V от замкнутой поверхности объема , охватывающего x _0, к объему V , поскольку V сжимается. до нуля

$\left.\operatorname {div} \mathbf {F} \right|_{\mathbf {x_{0}} }=\lim _{V\to 0}{\frac {1}{|V|}}$ $\scriptstyle S(V)$ $\mathbf {F} \cdot \mathbf {\hat {n}} \,dS$

где | В | — объем V , S ( V ) — граница V , а $\mathbf {\hat {n}}$ - внешняя единица, нормальная к этой поверхности. Можно показать, что приведенный выше предел всегда сходится к одному и тому же значению для любой последовательности объемов, которые содержат x ₀ и приближаются к нулевому объему. Результат, div F , является скалярной функцией x .

Поскольку это определение является бескоординатным, оно показывает, что расходимость одинакова в любой системе координат . Однако на практике для расчета дивергенции его используют нечасто; когда векторное поле задано в системе координат, определения координат, приведенные ниже, использовать намного проще.

Векторное поле с нулевой дивергенцией повсюду называется соленоидальным - в этом случае любая замкнутая поверхность не имеет чистого потока через нее.

Определение в координатах

Декартовы координаты

В трехмерных декартовых координатах дивергенция непрерывно дифференцируемого векторного поля $\mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k}$ определяется как скалярная функция:

$\operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} =\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot (F_{x},F_{y},F_{z})={\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}.$

Хотя результат и выражен в координатах, он инвариантен относительно вращений , как предполагает физическая интерпретация. Это связано с тем, что след матрицы Якоби -мерного N векторного поля F в N -мерном пространстве инвариантен относительно любого обратимого линейного преобразования. .

Общепринятое обозначение дивергенции ∇ · F представляет собой удобную мнемонику, где точка обозначает операцию, напоминающую скалярное произведение : возьмите компоненты оператора ∇ (см. del ), примените их к соответствующим компонентам F и просуммируйте результаты. Поскольку применение оператора отличается от умножения компонентов, это считается злоупотреблением обозначениями .

Цилиндрические координаты

Для вектора, выраженного в локальных единицах цилиндрических координат как

$\mathbf {F} =\mathbf {e} _{r}F_{r}+\mathbf {e} _{\theta }F_{\theta }+\mathbf {e} _{z}F_{z},$

где e _a — единичный вектор в направлении a , дивергенция равна

$\operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rF_{r}\right)+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}+{\frac {\partial F_{z}}{\partial z}}.$

Использование локальных координат жизненно важно для корректности выражения. Если мы рассмотрим x как вектор положения и функции r ( x ) , θ ( x ) и z ( x ) соответствующую глобальную цилиндрическую координату, в общем случае , которые присваивают вектору $r(\mathbf {F} (\mathbf {x} ))\neq F_{r}(\mathbf {x} )$, $\theta (\mathbf {F} (\mathbf {x} ))\neq F_{\theta }(\mathbf {x} )$, и $z(\mathbf {F} (\mathbf {x} ))\neq F_{z}(\mathbf {x} )$. В частности, если мы рассмотрим тождественную функцию F ( x ) = x , мы обнаружим, что:

$\theta (\mathbf {F} (\mathbf {x} ))=\theta \neq F_{\theta }(\mathbf {x} )=0$.

Сферические координаты

В сферических координатах , где θ - угол с осью z , φ - вращение вокруг оси z , а F снова записано в локальных единицах координат, расхождение равно

$\operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}F_{r}\right)+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta \,F_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial F_{\varphi }}{\partial \varphi }}.$

Тензорное поле

Пусть A второго порядка, — непрерывно дифференцируемое тензорное поле определяемое следующим образом:

$\mathbf {A} ={\begin{bmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{bmatrix}}$

дивергенция в декартовой системе координат представляет собой тензорное поле первого порядка и может быть определен двумя способами:

$\operatorname {div} (\mathbf {A} )={\cfrac {\partial A_{ik}}{\partial x_{k}}}~\mathbf {e} _{i}=A_{ik,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{12}}{\partial x_{2}}}+{\dfrac {\partial A_{13}}{\partial x_{3}}}\\{\dfrac {\partial A_{21}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{23}}{\partial x_{3}}}\\{\dfrac {\partial A_{31}}{\partial x_{1}}}+{\dfrac {\partial A_{32}}{\partial x_{2}}}+{\dfrac {\partial A_{33}}{\partial x_{3}}}\end{bmatrix}}$

и

$\nabla \cdot \mathbf {A} ={\cfrac {\partial A_{ki}}{\partial x_{k}}}~\mathbf {e} _{i}=A_{ki,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{21}}{\partial x_{2}}}+{\dfrac {\partial A_{31}}{\partial x_{3}}}\\{\dfrac {\partial A_{12}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{32}}{\partial x_{3}}}\\{\dfrac {\partial A_{13}}{\partial x_{1}}}+{\dfrac {\partial A_{23}}{\partial x_{2}}}+{\dfrac {\partial A_{33}}{\partial x_{3}}}\\\end{bmatrix}}$

У нас есть

$\operatorname {div} (\mathbf {A^{T}} )=\nabla \cdot \mathbf {A}$

Если тензор симметричен A _ij = A _ji , то $\operatorname {div} (\mathbf {A} )=\nabla \cdot \mathbf {A}$. По этой причине часто в литературе используются два определения (и символы div и $\nabla \cdot$) используются как взаимозаменяемые (особенно в уравнениях механики, где предполагается тензорная симметрия).

Выражения $\nabla \cdot \mathbf {A}$ в цилиндрических и сферических координатах приведены в статье del в цилиндрических и сферических координатах .

Общие координаты

Используя обозначения Эйнштейна, мы можем рассмотреть расхождение в общих координатах , которое мы запишем как x ¹ , …, х ^я , …, х ^н , где n — количество измерений области. Здесь верхний индекс относится к номеру координаты или компонента, поэтому x ² относится ко второму компоненту, а не к величине x в квадрате. Индексная переменная i используется для ссылки на произвольный компонент, например x ^я . Тогда дивергенцию можно записать с помощью формулы Восса - Вейля : как:

$\operatorname {div} (\mathbf {F} )={\frac {1}{\rho }}{\frac {\partial \left(\rho \,F^{i}\right)}{\partial x^{i}}},$

где $\rho$ — локальный коэффициент элемента объема , а F ^я являются компонентами $\mathbf {F} =F^{i}\mathbf {e} _{i}$ относительно локального ненормированного ковариантного базиса (иногда записываемого как $\mathbf {e} _{i}=\partial \mathbf {x} /\partial x^{i}$) . Обозначение Эйнштейна подразумевает суммирование по i , поскольку оно появляется как верхний, так и нижний индекс.

Коэффициент объема ρ является функцией положения, которая зависит от системы координат. В декартовых, цилиндрических и сферических координатах, используя те же соглашения, что и раньше, мы имеем ρ = 1 , ρ = r и ρ = r. ² грех θ соответственно. Объем также можно выразить как ${\textstyle \rho ={\sqrt {\left|\det g_{ab}\right|}}}$, где g _ab — метрический тензор . Определитель появляется потому , что он обеспечивает соответствующее инвариантное определение объема с учетом набора векторов. Поскольку определитель представляет собой скалярную величину, не зависящую от индексов, их можно опустить, записав ${\textstyle \rho ={\sqrt {\left|\det g\right|}}}$. Абсолютное значение берется для обработки общего случая, когда определитель может быть отрицательным, например, в псевдоримановых пространствах. Причина квадратного корня немного тонкая: он эффективно позволяет избежать двойного счета при переходе от кривых к декартовым координатам и обратно. Объем (определитель) можно понимать также как якобиан преобразования декартовых координат в криволинейные, что при n = 3 дает ${\textstyle \rho =\left|{\frac {\partial (x,y,z)}{\partial (x^{1},x^{2},x^{3})}}\right|}$.

Некоторые соглашения требуют, чтобы все локальные базисные элементы были нормализованы до единичной длины, как это было сделано в предыдущих разделах. Если мы напишем ${\hat {\mathbf {e} }}_{i}$ для нормализованной основы, и ${\hat {F}}^{i}$ для компонент F относительно него имеем

$\mathbf {F} =F^{i}\mathbf {e} _{i}=F^{i}\|{\mathbf {e} _{i}}\|{\frac {\mathbf {e} _{i}}{\|\mathbf {e} _{i}\|}}=F^{i}{\sqrt {g_{ii}}}\,{\hat {\mathbf {e} }}_{i}={\hat {F}}^{i}{\hat {\mathbf {e} }}_{i},$

используя одно из свойств метрического тензора. Поставив точку в обеих частях последнего равенства контравариантным элементом ${\hat {\mathbf {e} }}^{i}$, мы можем заключить, что ${\textstyle F^{i}={\hat {F}}^{i}/{\sqrt {g_{ii}}}}$. После замены формула примет вид:

$\operatorname {div} (\mathbf {F} )={\frac {1}{\rho }}{\frac {\partial \left({\frac {\rho }{\sqrt {g_{ii}}}}{\hat {F}}^{i}\right)}{\partial x^{i}}}={\frac {1}{\sqrt {\det g}}}{\frac {\partial \left({\sqrt {\frac {\det g}{g_{ii}}}}\,{\hat {F}}^{i}\right)}{\partial x^{i}}}.$

См . § В криволинейных координатах для дальнейшего обсуждения.

Свойства

Основная статья: Тождества векторного исчисления

Следующие свойства могут быть выведены из обычных правил дифференцирования исчисления . Самое главное, что дивергенция является линейным оператором , т. е.

$\operatorname {div} (a\mathbf {F} +b\mathbf {G} )=a\operatorname {div} \mathbf {F} +b\operatorname {div} \mathbf {G}$

для всех векторных полей F и G и всех действительных чисел a и b .

Существует правило произведения следующего типа: если φ — скалярная функция, а F — векторное поле, то

$\operatorname {div} (\varphi \mathbf {F} )=\operatorname {grad} \varphi \cdot \mathbf {F} +\varphi \operatorname {div} \mathbf {F} ,$

или в более наводящих на размышления обозначениях

$\nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi (\nabla \cdot \mathbf {F} ).$

Другое правило произведения для векторного произведения двух векторных полей F и G в трех измерениях включает в себя ротор и гласит следующее:

$\operatorname {div} (\mathbf {F} \times \mathbf {G} )=\operatorname {curl} \mathbf {F} \cdot \mathbf {G} -\mathbf {F} \cdot \operatorname {curl} \mathbf {G} ,$

или

$\nabla \cdot (\mathbf {F} \times \mathbf {G} )=(\nabla \times \mathbf {F} )\cdot \mathbf {G} -\mathbf {F} \cdot (\nabla \times \mathbf {G} ).$

Лапласиан — это скалярного поля поля дивергенция градиента :

$\operatorname {div} (\operatorname {grad} \varphi )=\Delta \varphi .$

Дивергенция ротора любого векторного поля (в трёх измерениях) равна нулю:

$\nabla \cdot (\nabla \times \mathbf {F} )=0.$

Если векторное поле F с нулевой дивергенцией определено на шаре в R ³ существует некоторое векторное поле G , то на шаре такое, что F = rot G . Для регионов в R ³ более топологически сложное, чем это, последнее утверждение может быть ложным (см. лемму Пуанкаре ). Степень ошибочности истинности утверждения, измеряемая гомологией цепного комплекса .

$\{{\text{scalar fields on }}U\}~{\overset {\operatorname {grad} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {curl} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {div} }{\rightarrow }}~\{{\text{scalar fields on }}U\}$

служит хорошей количественной оценкой сложности лежащего в основе региона U . Таковы начала и основные мотивы когомологий де Рама .

Теорема

Основная статья: разложение Гельмгольца

Можно показать, что любой стационарный поток v ( r ) , дважды непрерывно дифференцируемый в R ³ и исчезает достаточно быстро при | р | → ∞ можно однозначно разложить на безвихревую часть E ( r ) и часть без источника B ( r ) . Более того, эти части явно определяются соответствующими плотностями источников (см. выше) и плотностью циркуляции (см. статью Curl ):

Для безвихревой части имеется

$\mathbf {E} =-\nabla \Phi (\mathbf {r} ),$

с

$\Phi (\mathbf {r} )=\int _{\mathbb {R} ^{3}}\,d^{3}\mathbf {r} '\;{\frac {\operatorname {div} \mathbf {v} (\mathbf {r} ')}{4\pi \left|\mathbf {r} -\mathbf {r} '\right|}}.$

Часть, не содержащая источников, B , может быть записана аналогично: нужно только заменить скалярный потенциал Φ( r ) векторным потенциалом A ( r ) , члены −∇Φ на +∇ × A , а плотность источника div в плотностью циркуляции ∇ × v .

Эта «теорема о разложении» является побочным продуктом стационарного случая электродинамики . Это частный случай более общего разложения Гельмгольца , которое работает и в размерностях больше трех.

В произвольных конечных размерах

Дивергенцию векторного поля можно определить в любом конечном числе $n$ размеров. Если

$\mathbf {F} =(F_{1},F_{2},\ldots F_{n}),$

в евклидовой системе координат с координатами x ₁ , x ₂ , ..., x _n , определим

$\operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial F_{1}}{\partial x_{1}}}+{\frac {\partial F_{2}}{\partial x_{2}}}+\cdots +{\frac {\partial F_{n}}{\partial x_{n}}}.$

В одномерном случае F сводится к регулярной функции, а дивергенция – к производной.

Для любого n дивергенция является линейным оператором и удовлетворяет «правилу произведения».

$\nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi (\nabla \cdot \mathbf {F} )$

для любой скалярной функции φ .

Связь с внешней производной

Дивергенцию можно выразить как частный случай внешней производной , которая переводит 2-форму в 3-форму в R ³ . Определите текущую двухформу как

$j=F_{1}\,dy\wedge dz+F_{2}\,dz\wedge dx+F_{3}\,dx\wedge dy.$

Он измеряет количество «вещества», протекающего через поверхность в единицу времени в «вещественной жидкости» плотности ρ = 1 dx ∧ dy ∧ dz, движущейся с локальной скоростью F . Тогда его внешняя производная dj будет равна

$dj=\left({\frac {\partial F_{1}}{\partial x}}+{\frac {\partial F_{2}}{\partial y}}+{\frac {\partial F_{3}}{\partial z}}\right)dx\wedge dy\wedge dz=(\nabla \cdot {\mathbf {F} })\rho$

где $\wedge$ это клиновое произведение .

Таким образом, дивергенцию векторного поля F можно выразить как:

$\nabla \cdot {\mathbf {F} }={\star }d{\star }{\big (}{\mathbf {F} }^{\flat }{\big )}.$

Здесь верхний индекс ♭ — это один из двух музыкальных изоморфизмов , а ⋆ — оператор звезды Ходжа . При такой записи дивергенции оператор ${\star }d{\star }$ называется кодифференциалом . Работать с текущей двухформой и внешней производной обычно проще, чем с векторным полем и дивергенцией, поскольку в отличие от дивергенции внешняя производная коммутирует с изменением (криволинейной) системы координат.

В криволинейных координатах

Соответствующее выражение более сложное в криволинейных координатах . Дивергенция векторного поля естественным образом распространяется на любое дифференцируемое многообразие размерности n , имеющее форму объема (или плотность ) µ , например риманово или лоренцево многообразие . Обобщая конструкцию двухформ векторного поля на R ³ , на таком многообразии векторное поле X определяет ( n − 1) -форму j = i _X   µ, полученную стягиванием X с µ . Тогда дивергенция представляет собой функцию, определяемую формулой

$dj=(\operatorname {div} X)\mu .$

Дивергенцию можно определить через производную Ли как

${\mathcal {L}}_{X}\mu =(\operatorname {div} X)\mu .$

Это означает, что дивергенция измеряет скорость расширения единицы объема ( элемента объема ) при ее движении вместе с векторным полем.

На псевдоримановом многообразии дивергенция по объему может быть выражена через связность Леви-Чивита ∇ :

$\operatorname {div} X=\nabla \cdot X={X^{a}}_{;a},$

где второе выражение представляет собой сжатие векторного поля со значением 1-формы ∇ X с самим собой, а последнее выражение представляет собой традиционное координатное выражение из исчисления Риччи .

Эквивалентное выражение без использования соединения:

$\operatorname {div} (X)={\frac {1}{\sqrt {\left|\det g\right|}}}\,\partial _{a}\left({\sqrt {\left|\det g\right|}}\,X^{a}\right),$

где g — метрика и $\partial _{a}$ обозначает частную производную по координате x ^а . Квадратный корень из (абсолютного значения определителя ) метрики появляется потому, что расхождение должно быть записано с правильным представлением об объеме . В криволинейных координатах базисные векторы больше не являются ортонормированными; в этом случае определитель кодирует правильное представление об объеме. Оно появляется дважды, здесь, один раз, так что $X^{a}$ можно преобразовать в «плоское пространство» (где координаты на самом деле ортонормированы), и еще раз так, что $\partial _{a}$ также преобразуется в «плоское пространство», так что, наконец, «обычное» расхождение можно записать с помощью «обычного» понятия объема в плоском пространстве ( т.е. единицы объема, т.е. единицы, т.е. не записанной). Квадратный корень появляется в знаменателе, потому что производная преобразуется противоположным образом ( контравариантно ) вектору (который является ковариантным ). Эта идея перехода к «плоской системе координат», в которой локальные вычисления могут выполняться обычным способом, называется vielbein . Другой способ увидеть это — заметить, что дивергенция — это кодифференциал замаскированный . То есть расхождение соответствует выражению $\star d\star$ с $d$ дифференциал ​ и $\star$ звезда Ходжа . Звезда Ходжа по своей конструкции заставляет объемную форму появляться во всех нужных местах.

Расхождение тензоров

Дивергенцию также можно обобщить на тензоры . В обозначениях Эйнштейна дивергенция контравариантного вектора F ^м дается

$\nabla \cdot \mathbf {F} =\nabla _{\mu }F^{\mu },$

где ∇ _µ обозначает ковариантную производную . В этой общей ситуации правильная формулировка дивергенции состоит в том, чтобы признать, что она является кодифференциалом ; оттуда следуют соответствующие свойства.

некоторые авторы определяют дивергенцию смешанного тензора , используя музыкальный изоморфизм ♯ : если T является ( p , q ) -тензором Аналогичным образом , ( p для контравариантного вектора и q для ковариантного), то мы определяем дивергенцию T быть ( p , q − 1) -тензором

$(\operatorname {div} T)(Y_{1},\ldots ,Y_{q-1})={\operatorname {trace} }{\Big (}X\mapsto \sharp (\nabla T)(X,\cdot ,Y_{1},\ldots ,Y_{q-1}){\Big )};$

то есть мы берем след по первым двум ковариантным индексам ковариантной производной. $\sharp$ Символ относится к музыкальному изоморфизму .

См. также

• Завиток
• Del в цилиндрических и сферических координатах
• Теорема о дивергенции
• Градиент

Ссылки

• Брюэр, Джесс Х. (1999). «ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ» . musr.phas.ubc.ca. ​Архивировано из оригинала 23 ноября 2007 г. Проверено 9 августа 2016 г.
• Рудин, Уолтер (1976). Принципы математического анализа . МакГроу-Хилл. ISBN  0-07-054235-Х .
• Эдвардс, Швейцария (1994). Расширенное исчисление нескольких переменных . Минеола, Нью-Йорк: Дувр. ISBN  0-486-68336-2 .
• Гуртин, Мортон (1981). Введение в механику сплошных сред . Академическая пресса. ISBN  0-12-309750-9 .
• Корн, Тереза ​​М .; Корн, Гранино Артур (январь 2000 г.). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора . Нью-Йорк: Dover Publications. стр. 157–160. ISBN  0-486-41147-8 .

Внешние ссылки

• «Дивергенция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Идея дивергенции векторного поля
• Академия Хана: видеоурок «Дивергенция»
• Сандерсон, Грант (21 июня 2018 г.). «Дивергенция и завиток: язык уравнений Максвелла, течения жидкости и многого другого» . 3Синий1Коричневый . Архивировано из оригинала 11 декабря 2021 г. – на YouTube .