ряд Фурье
| Преобразования Фурье |
|---|
Ряд Фурье ( / ˈ f ʊr i eɪ , - i ər / [1] ) — разложение периодической функции в сумму тригонометрических функций . Ряд Фурье является примером тригонометрического ряда , но не все тригонометрические ряды являются рядами Фурье. [2] Выражая функцию в виде суммы синусов и косинусов, многие проблемы, связанные с этой функцией, становится легче анализировать, поскольку тригонометрические функции хорошо изучены. Например, ряды Фурье впервые были использованы Жозефом Фурье для поиска решений уравнения теплопроводности . Такое применение возможно, поскольку производные тригонометрических функций распадаются на простые закономерности. Ряды Фурье нельзя использовать для аппроксимации произвольных функций, поскольку большинство функций имеют в своих рядах Фурье бесконечное число членов, и эти ряды не всегда сходятся . Функции с хорошим поведением, например гладкие функции, имеют ряды Фурье, которые сходятся к исходной функции. Коэффициенты ряда Фурье определяются интегралами функции, умноженной на тригонометрические функции, описанные ниже в разделе « Общие формы ряда Фурье» .
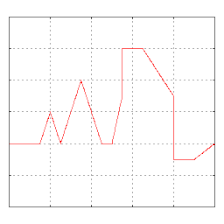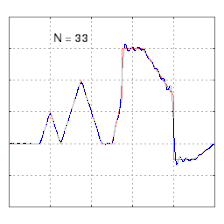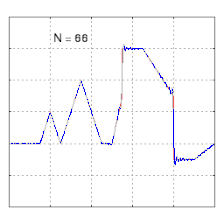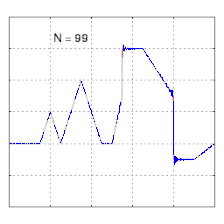
Изучение сходимости рядов Фурье сосредоточено на поведении частичных сумм , что означает изучение поведения суммы по мере того, как суммируются все больше и больше членов ряда. На рисунках ниже показаны некоторые частичные результаты рядов Фурье для компонентов прямоугольной волны .
- Прямоугольная волна (представленная синей точкой) аппроксимируется своей шестой частичной суммой (представленной фиолетовой точкой), образованной суммированием первых шести членов (представленных стрелками) ряда Фурье прямоугольной волны. Каждая стрелка начинается с вертикальной суммы всех стрелок слева от нее (т. е. предыдущей частичной суммы).
- Первые четыре частичные суммы ряда Фурье для прямоугольной волны . По мере добавления большего количества гармоник частичные суммы сходятся (становятся все более и более похожими) на прямоугольную волну.
- Функция (красным цветом) представляет собой сумму ряда Фурье шести гармонически связанных синусоидальных волн (синим цветом). Его преобразование Фурье представляет собой представление в частотной области, которое показывает амплитуды суммированных синусоидальных волн.
Ряды Фурье тесно связаны с преобразованием Фурье , которое можно использовать для поиска информации о частоте для функций, которые не являются периодическими. Периодические функции можно отождествить с функциями на окружности; по этой причине ряды Фурье являются предметом анализа Фурье на окружности, обычно обозначаемой как или . Преобразование Фурье также является частью анализа Фурье , но оно определено для функций на .
Со времен Фурье было открыто множество различных подходов к определению и пониманию понятия ряда Фурье, все из которых согласуются друг с другом, но каждый из которых подчеркивает разные аспекты темы. Некоторые из наиболее мощных и элегантных подходов основаны на математических идеях и инструментах, которых не было во времена Фурье. Первоначально Фурье определил ряд Фурье для действительных функций от действительных аргументов и использовал функции синуса и косинуса при разложении многие другие преобразования Фурье . С тех пор были определены , что расширило его первоначальную идею на многие приложения и положило начало области математики, называемой анализом Фурье .
ряда Фурье Общие формы
Ряд Фурье — это непрерывная периодическая функция, созданная суммированием гармонически связанных синусоидальных функций. Он имеет несколько разных, но эквивалентных форм, показанных здесь как частичные суммы. Но теоретически Подстрочные символы, называемые коэффициентами , и период, определить функцию следующее :

| ( Уравнение 1 ) |
| ( Уравнение 2 ) |
| ( Уравнение 3 ) |
Гармоники индексируются целым числом, что также является количеством циклов, которые делают соответствующие синусоиды за интервал . Следовательно, синусоиды имеют :
Очевидно, что эти ряды могут представлять функции, которые представляют собой просто сумму одной или нескольких частот гармоник. Примечательно то, что он также может представлять промежуточные частоты и/или несинусоидальные функции из-за бесконечного числа членов. Амплитудно-фазовая форма особенно полезна для понимания смысла коэффициентов ряда. (см. § Вывод ). Показательную форму легче всего обобщить для комплекснозначных функций. (см. § Комплекснозначные функции )
Эквивалентность этих форм требует определенных соотношений между коэффициентами. Например, тригонометрическое тождество :
означает, что :
| ( Уравнение 4.1 ) |
Поэтому и — прямоугольные координаты вектора с полярными координатами и
Коэффициенты могут быть заданы/предполагаемы, например, музыкальный синтезатор или временные выборки формы волны. В последнем случае экспоненциальная форма ряда Фурье синтезирует преобразование Фурье с дискретным временем , где переменная представляет частоту вместо времени.
Но обычно коэффициенты определяются путем частотного/гармонического анализа данной действительной функции. и представляет время :
| ( Уравнение 5 ) |
Цель состоит в том, чтобы сходиться к максимум или все значения в интервале длины Для корректных функций, типичных для физических процессов, обычно предполагается равенство, а условия Дирихле обеспечивают достаточные условия.
Обозначения представляет собой интегрирование по выбранному интервалу. Типичный выбор: и . Некоторые авторы определяют потому что это упрощает аргументы синусоидальных функций за счет общности. И некоторые авторы полагают, что также -периодический, в этом случае аппроксимирует всю функцию. Коэффициент масштабирования объясняется на простом примере : Только член уравнения 2 необходим для сходимости, при этом и Соответственно уравнение 5 дает :
- по мере необходимости.
Коэффициенты экспоненциальной формы
Другим применимым тождеством является формула Эйлера :
(Примечание : * обозначает комплексное сопряжение .)
Подстановка этого значения в уравнение 1 и сравнение с уравнением 3 в конечном итоге показывает :
| ( Уравнение 6 ) |
И наоборот :
Подстановка уравнения 5 в уравнение 6 также показывает : [3]
( все целые числа ) | ( Уравнение 7 ) |
Комплексные функции [ править ]
Уравнения 7 и 3 также применимы, когда является комплексной функцией. [А] Это следует из выражения и как отдельные действительные ряды Фурье, и
Вывод [ править ]
Коэффициенты и можно понять и вывести с точки зрения взаимной корреляции между и синусоида на частоте . Для общей частоты и интервал анализа функция взаимной корреляции :

| ( Уравнение 8 ) |
по сути, это согласованный фильтр с шаблоном .Максимум является мерой амплитуды частоты в функции , и значение в максимуме определяет фазу этой частоты. На рисунке 2 приведен пример, где представляет собой прямоугольную волну (не показана), а частота это гармонический. Это также пример получения максимума всего из двух выборок вместо поиска по всей функции. Объединение уравнения 8 с уравнением 4 дает :
Производная от равен нулю в фазе максимальной корреляции.
Следовательно, вычисление и согласно уравнению 5 создает фазу компонента максимальной корреляции. А амплитуда компонента равна :
Другие распространенные обозначения [ править ]
Обозначения недостаточно для обсуждения коэффициентов Фурье нескольких различных функций. Поэтому ее принято заменять модифицированной формой функции ( в данном случае), например или , а функциональная запись часто заменяет индекс :
В технике, особенно когда переменная представляет время, последовательность коэффициентов называется представлением в частотной области . Квадратные скобки часто используются, чтобы подчеркнуть, что областью определения этой функции является дискретный набор частот.
Другое часто используемое представление в частотной области использует коэффициенты ряда Фурье для модуляции гребенки Дирака :
где представляет собой непрерывную частотную область. Когда переменная имеет единицы секунды, имеет единицы герцы . «Зубцы» гребенки расположены на расстоянии, кратном (т.е. гармоникам ) , которая называется основной частотой . может быть восстановлено из этого представления с помощью обратного преобразования Фурье :
Построенная функция поэтому его обычно называют преобразованием Фурье , хотя интеграл Фурье периодической функции не сходится на частотах гармоник. [Б]
Пример анализа [ править ]


Рассмотрим пилообразную функцию :
В этом случае коэффициенты Фурье имеют вид
Можно показать, что ряд Фурье сходится к в каждой точке где дифференцируема, поэтому :
| ( Уравнение 9 ) |
Когда , ряд Фурье сходится к 0, что является полусуммой левого и правого пределов s в точке . Это частный случай теоремы Дирихле для рядов Фурье.
Этот пример приводит к решению Базельской проблемы .
Конвергенция [ править ]
Доказательство того, что ряд Фурье является допустимым представлением любой периодической функции (которая удовлетворяет условиям Дирихле ), представлено в § Теорема Фурье, доказывающая сходимость рядов Фурье .
В инженерных приложениях обычно предполагается, что ряд Фурье сходится, за исключением скачков, поскольку функции, встречающиеся в инженерии, ведут себя лучше, чем функции, встречающиеся в других дисциплинах. В частности, если является непрерывным и является производной от (которая может существовать не везде) интегрируема с квадратом, то ряд Фурье сходится абсолютно и равномерно к . [4] Если функция интегрируема с квадратом на интервале , то ряд Фурье сходится к функции почти всюду . Можно определить коэффициенты Фурье для более общих функций или распределений, и в этом случае точечная сходимость часто не удается, и сходимость по норме или слабая сходимость обычно изучается .
- Четыре частичные суммы (ряд Фурье) длин 1, 2, 3 и 4 члена, показывающие, как аппроксимация прямоугольной волны улучшается по мере увеличения количества членов (анимация)
- Четыре частичные суммы (ряд Фурье) длин 1, 2, 3 и 4 члена, показывающие, как приближение к пилообразной волне улучшается по мере увеличения количества членов (анимация)
- Пример сходимости к несколько произвольной функции. Обратите внимание на развитие «звона» ( феномена Гиббса ) при переходах на вертикальные участки и обратно.
История [ править ]
Ряд Фурье назван в честь Жана-Батиста Жозефа Фурье (1768–1830), который внес важный вклад в изучение тригонометрических рядов , после предварительных исследований Леонарда Эйлера , Жана ле Рона д'Аламбера и Даниэля Бернулли . [С] Фурье ввел этот ряд с целью решения уравнения теплопроводности в металлической пластине, опубликовав свои первоначальные результаты в своем «Mémoire sur la propagation de la chaleur dans les Corps Solides » ( Трактат о распространении тепла в твердых телах ) 1807 года и опубликовав свою работу. Théorie analytique de la chaleur ( Аналитическая теория тепла ) в 1822 году. В «Мемуаре» был представлен анализ Фурье, в частности ряд Фурье. Исследованиями Фурье был установлен факт, что произвольная (сначала непрерывная) [5] а затем обобщается на любые кусочно -гладкие [6] ) функция может быть представлена тригонометрическим рядом. Первое заявление об этом великом открытии было сделано Фурье в 1807 году перед Французской академией . [7] Ранние идеи разложения периодической функции в сумму простых осциллирующих функций относятся к III веку до нашей эры, когда древние астрономы предложили эмпирическую модель движения планет, основанную на деферентах и эпициклах .
Уравнение теплопроводности представляет собой уравнение в частных производных . До работы Фурье не было известно решение уравнения теплопроводности в общем случае, хотя были известны частные решения, если источник тепла вел себя простым образом, в частности, если источником тепла была синусоидальная или косинусоидальная волна . Эти простые решения теперь иногда называют собственными решениями . Идея Фурье заключалась в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию ) простых синусоидальных и косинусоидальных волн и записать решение как суперпозицию соответствующих собственных решений . Эта суперпозиция или линейная комбинация называется рядом Фурье.
С современной точки зрения результаты Фурье несколько неформальны из-за отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позже Питер Густав Лежен Дирихле [8] и Бернхард Риман [9] [10] [11] выразил результаты Фурье с большей точностью и формальностью.
Хотя первоначальная мотивация заключалась в решении уравнения теплопроводности, позже стало очевидно, что те же методы можно применить к широкому кругу математических и физических задач, особенно к тем, которые включают линейные дифференциальные уравнения с постоянными коэффициентами, для которых собственные решения являются синусоидами . Ряд Фурье имеет множество таких применений в электротехнике , вибрационном анализе, акустике , оптике , обработке сигналов , обработке изображений , квантовой механике , эконометрике , [12] теория оболочек , [13] и т. д.
Начало [ править ]
Жозеф Фурье писал: [ сомнительно ]
Умножив обе части на , а затем интегрируя из к дает:
Это немедленно дает любой коэффициент a k тригонометрического ряда для φ( y ) для любой функции, имеющей такое разложение. Это работает, потому что если φ имеет такое разложение, то (при подходящих предположениях о сходимости) интеграл
В этих нескольких строках, близких к современному формализму, используемому в рядах Фурье, Фурье произвел революцию как в математике, так и в физике. Хотя подобные тригонометрические ряды ранее использовались Эйлером , Даламбером , Даниэлем Бернулли и Гауссом , Фурье считал, что такие тригонометрические ряды могут представлять любую произвольную функцию. В каком смысле это на самом деле верно – вопрос довольно тонкий, и многолетние попытки прояснить эту идею привели к важным открытиям в теориях сходимости , функциональных пространствах и гармоническом анализе .
Когда Фурье представил позднее конкурсное эссе в 1811 году, комитет (в который, среди прочих, входили Лагранж , Лаплас , Малюс и Лежандр ) пришел к выводу: ...способ, которым автор пришел к этим уравнениям, не лишен трудностей и... его анализ по их объединению все еще оставляет желать лучшего с точки зрения общности и даже строгости . [ нужна ссылка ]
Мотивация Фурье [ править ]

Разложение пилообразной функции в ряд Фурье (вверху) выглядит сложнее, чем простая формула , поэтому не сразу понятно, зачем нужен ряд Фурье. Хотя существует множество приложений, мотивацией Фурье было решение уравнения теплопроводности . Например, рассмотрим металлическую пластину в форме квадрата, стороны которого равны метров, с координатами . Если внутри пластины нет источника тепла и если на трех из четырех сторон поддерживается температура 0 градусов Цельсия, а на четвертой стороне, определяемой выражением , поддерживается при градиенте температуры градусов Цельсия, для в , то можно показать, что стационарное распределение тепла (или распределение тепла по истечении длительного периода времени) определяется выражением
Здесь sinh — гиперболический синус. Это решение уравнения теплопроводности получается путем умножения каждого члена уравнения 9 на . Хотя наш пример функции кажется, имеет излишне сложный ряд Фурье, распределение тепла является нетривиальным. Функция не может быть записано как выражение закрытой формы . Этот метод решения тепловой проблемы стал возможен благодаря работе Фурье.
сложного Анимация ряда Фурье
Пример способности комплексного ряда Фурье отслеживать любую двумерную замкнутую фигуру показан в соседней анимации комплексного ряда Фурье, отслеживающего букву «е» (для экспоненты). Обратите внимание, что анимация использует переменную «t» для параметризации буквы «e» в комплексной плоскости, что эквивалентно использованию параметра «x» в подразделе этой статьи, посвященном функциям с комплексными значениями.
В задней плоскости анимации вращающиеся векторы объединяются в порядке, который чередуется между вектором, вращающимся в положительном (против часовой стрелки) направлении, и вектором, вращающимся с той же частотой, но в отрицательном (по часовой стрелке) направлении, в результате чего получается единая трассировка. рука с множеством зигзагов. Эта перспектива показывает, как добавление каждой пары вращающихся векторов (один вращается в положительном направлении, а другой вращается в отрицательном направлении) подталкивает предыдущий след (показанный светло-серой пунктирной линией) ближе к форме буквы «е». .
В передней плоскости анимации вращающиеся векторы объединяются в два набора: набор всех положительных вращающихся векторов и набор всех отрицательных вращающихся векторов (невращающийся компонент равномерно разделен между ними), в результате чего получаются две трассировки. руки вращаются в противоположные стороны. Маленький кружок анимации обозначает среднюю точку между двумя плечами, а также среднюю точку между началом координат и текущей точкой трассировки, обозначенную знаком «+». Эта перспектива показывает, как комплексный ряд Фурье является расширением (добавлением плеча) сложного геометрического ряда, имеющего только одно плечо. Это также показывает, как две руки координируются друг с другом. Например, поскольку точка трассировки вращается в положительном направлении, рычаг отрицательного направления остается неподвижным. Аналогично, когда точка отслеживания вращается в отрицательном направлении, рычаг положительного направления остается неподвижным.
Между задней и передней плоскостями анимации находятся вращающиеся трапеции, площади которых представляют значения членов комплексного ряда Фурье. Эта перспектива показывает амплитуду, частоту и фазу отдельных членов комплексного ряда Фурье по отношению к сумме ряда, пространственно сходящейся к букве «е» в задней и передней плоскостях. Левый и правый каналы звуковой дорожки соответствуют соответственно реальному и мнимому компонентам текущей точки трассировки «+», но их частота увеличена в 3536 раз, так что основная частота анимации (n=1) представляет собой тон 220 Гц (A220 ).
Другие приложения [ править ]
Другое применение — решение Базельской задачи с помощью теоремы Парсеваля . Пример обобщает, и можно вычислить ζ (2 n ) для любого положительного целого числа n .
Таблица обычных Фурье рядов
Некоторые распространенные пары периодических функций и их коэффициенты ряда Фурье показаны в таблице ниже.
- обозначает периодическую функцию с периодом .
- обозначим коэффициенты ряда Фурье (синус-косинусной формы) периодической функции .
| Временной интервал | Сюжет | Частотная область (синус-косинусная форма) | Примечания | Ссылка |
|---|---|---|---|---|
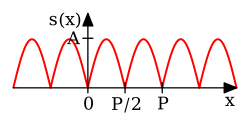 | Полноволновой выпрямленный синус | [16] : с. 193 | ||
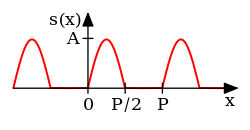 | Полуволновой выпрямленный синус | [16] : с. 193 | ||
 | ||||
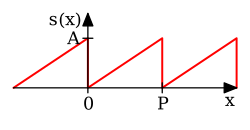 | [16] : с. 192 | |||
 | [16] : с. 192 | |||
 | [16] : с. 193 |
Таблица основных свойств [ править ]
В этой таблице показаны некоторые математические операции во временной области и соответствующий эффект в коэффициентах ряда Фурье. Обозначение:
- Комплексное сопряжение отмечено звездочкой.
- назначать -периодические функции или функции, определенные только для
- обозначим коэффициенты ряда Фурье (экспоненциальной формы) и
| Свойство | Временной интервал | Частотная область (экспоненциальная форма) | Примечания | Ссылка |
|---|---|---|---|---|
| Линейность | ||||
| Обращение времени/Обращение частоты | [17] : с. 610 | |||
| Сопряжение времени | [17] : с. 610 | |||
| Обращение времени и сопряжение | ||||
| Реальная часть времени | ||||
| Мнимая часть времени | ||||
| Действительная часть по частоте | ||||
| Мнимая часть частоты | ||||
| Сдвиг во времени/Модуляция по частоте | [17] : стр.610 | |||
| Сдвиг частоты/модуляция во времени | [17] : с. 610 |
Свойства симметрии [ править ]
Когда действительная и мнимая части сложной функции разлагаются на четные и нечетные части , получается четыре компонента, обозначенные ниже индексами RE, RO, IE и IO. Между четырьмя компонентами комплексной функции времени и четырьмя компонентами ее комплексного частотного преобразования существует взаимно однозначное соответствие: [18]
Отсюда выявляются различные зависимости, например:
- Преобразованием вещественной функции ( s RE + s RO ) является четная симметричная функция S RE + i S IO . И наоборот, четно-симметричное преобразование подразумевает вещественную временную область.
- Преобразование мнимой функции ( i s IE + i s IO ) является нечетной симметричной функцией S RO + i S IE , и обратное верно.
- Преобразование четно-симметричной функции ( s RE + i s IO ) является действительной функцией S RE + S RO , и обратное верно.
- Преобразование нечетно-симметричной функции ( s RO + i s IE ) является мнимозначной функцией i S IE + i S IO , и обратное верно.
Другая недвижимость [ править ]
Лемма Римана–Лебега [ править ]
Если является интегрируемым , , и Этот результат известен как лемма Римана–Лебега .
Теорема Парсеваля [ править ]
Если принадлежит (периодический на интервале длины ) затем :
Теорема Планшереля [ править ]
Если являются коэффициентами и тогда есть уникальная функция такой, что для каждого .
Теоремы свертки
Данный -периодические функции, и с коэффициентами ряда Фурье и
- Точечное произведение : также -периодический, а коэффициенты его ряда Фурье задаются дискретной сверткой и последовательности :
- Периодическая свертка : также -периодический, с коэффициентами ряда Фурье :
- Двойно бесконечная последовательность в – это последовательность коэффициентов Фурье функции из тогда и только тогда, когда это свертка двух последовательностей в . Видеть [19]
Производное свойство [ править ]
Мы говорим, что принадлежит если является 2 π -периодической функцией на который раз дифференцируема, и ее производная непрерывна.
- Если , то коэффициенты Фурье производной может быть выражено через коэффициенты Фурье функции , по формуле .
- Если , затем . В частности, поскольку для фиксированного у нас есть как , отсюда следует, что стремится к нулю, а это означает, что коэффициенты Фурье сходятся к нулю быстрее, чем k -я степень n при любом .
Компактные группы [ править ]
Одним из интересных свойств преобразования Фурье, о котором мы упомянули, является то, что оно выполняет свертки с точечными произведениями. Если это свойство, которое мы стремимся сохранить, то можно построить ряд Фурье на любой компактной группе . Типичные примеры включают те классические группы , которые компактны. Это обобщает преобразование Фурье на все пространства вида L 2 ( G ), где G — компактная группа, таким образом, что преобразование Фурье переносит свертки в поточечные произведения. Ряд Фурье существует и сходится аналогично случаю [− π , π ] .
Альтернативным расширением компактных групп является теорема Питера-Вейля , которая доказывает результаты о представлениях компактных групп, аналогичные таковым о конечных группах.

Римановы многообразия [ править ]
Если домен не является группой, то не существует внутренне определенной свертки. Однако, если — компактное риманово многообразие , оно имеет оператор Лапласа–Бельтрами . Оператор Лапласа–Бельтрами — это дифференциальный оператор, соответствующий оператору Лапласа для риманова многообразия. . Тогда по аналогии можно рассмотреть уравнения теплопроводности на . Поскольку Фурье пришел к своему базису, пытаясь решить уравнение теплопроводности, естественным обобщением является использование в качестве основы собственных решений оператора Лапласа – Бельтрами. Это обобщает ряды Фурье на пространства типа , где является римановым многообразием. Ряд Фурье сходится аналогично случай. Типичный пример — взять быть сферой с обычной метрикой, и в этом случае базис Фурье состоит из сферических гармоник .
абелевы Локально компактные группы
Обсужденное выше обобщение на компактные группы не распространяется на некомпактные неабелевы группы . Однако существует прямое обобщение на локально компактные абелевы группы (LCA) .
Это обобщает преобразование Фурье до или , где является группой LCA. Если компактен, то также получается ряд Фурье, сходящийся аналогично случай, но если некомпактно, вместо этого получается интеграл Фурье . Это обобщение дает обычное преобразование Фурье , когда лежащая в основе локально компактная абелева группа равна .
Расширения [ править ]
Ряд Фурье по квадрату [ править ]
Мы также можем определить ряд Фурье для функций двух переменных и на площади :
Помимо того, что ряд Фурье по квадрату полезен для решения уравнений в частных производных, таких как уравнение теплопроводности, одним из заметных применений ряда Фурье по квадрату является сжатие изображений . В частности, стандарт сжатия изображений JPEG использует двумерное дискретное косинусное преобразование — дискретную форму косинусного преобразования Фурье , которая в качестве базовой функции использует только косинус.
Для двумерных массивов с шахматным видом половина коэффициентов ряда Фурье исчезает из-за дополнительной симметрии. [20]
Ряд Фурье решеточно- периодической функции Браве
Трехмерная решетка Браве определяется как набор векторов вида:
Таким образом, мы можем определить новую функцию,
Эта новая функция, , теперь является функцией трех переменных, каждая из которых имеет периодичность , , и соответственно:
Это позволяет нам построить набор коэффициентов Фурье, каждый из которых индексируется тремя независимыми целыми числами. . Далее для обозначения этих коэффициентов мы будем использовать функциональные обозначения, тогда как ранее мы использовали индексы. Если мы напишем серию для на интервале для , мы можем определить следующее:
И тогда мы можем написать:
Дальнейшее определение:
Мы можем написать еще раз как:
Наконец, применив то же самое к третьей координате, мы определяем:
Мы пишем как:
Перестановка:
Теперь каждый вектор обратной решетки можно записать (но это не означает, что это единственный способ записи) как , где являются целыми числами и являются векторами обратной решетки, удовлетворяющими ( для , и для ). Тогда для любого произвольного вектора обратной решетки и произвольный вектор положения в исходном пространстве решетки Браве их скалярное произведение равно:
Итак, ясно, что в нашем расширении , сумма на самом деле ведется по векторам обратной решетки:
где
Предполагая
(может быть выгодно в целях упрощения расчетов работать в такой прямоугольной системе координат, в которой так уж получилось, что параллельно оси x , лежит в плоскости xy , а имеет компоненты всех трех осей). Знаменатель - это в точности объем примитивной элементарной ячейки, заключенной в три примитивных вектора. , и . В частности, теперь мы знаем, что
Мы можем написать сейчас как интеграл с традиционной системой координат по объему примитивной ячейки, а не с , и переменные:
пространства Интерпретация гильбертова
На языке гильбертовых пространств множество функций является ортонормированным базисом пространства функций, интегрируемых с квадратом на . Это пространство на самом деле является гильбертовым пространством со скалярным произведением, заданным для любых двух элементов. и к:
- где представляет собой комплексное сопряжение
Основной результат ряда Фурье для гильбертовых пространств можно записать как

Это в точности соответствует комплексной экспоненциальной формулировке, приведенной выше. Версия с синусами и косинусами обоснована и интерпретацией гильбертова пространства. Действительно, синусы и косинусы образуют ортогональный набор :
доказывающая сходимость рядов Фурье Фурье , Теорема
Эти теоремы и их неформальные вариации, в которых не указаны условия сходимости, иногда в общем называются теоремой Фурье или теоремой Фурье . [21] [22] [23] [24]
Предыдущее уравнение 3 :
представляет собой тригонометрический полином степени в общем виде это можно выразить так :
Свойство наименьших квадратов [ править ]
Теорема Парсеваля подразумевает, что:
Теорема . Тригонометрический полином. — единственный лучший тригонометрический полином степени аппроксимирующий , в том смысле, что для любого тригонометрического полинома степени , у нас есть:
Теоремы сходимости
Благодаря свойству метода наименьших квадратов и полноте базиса Фурье мы получаем элементарный результат сходимости.
Теорема — Если принадлежит (интервал длиной ), затем сходится к в , то есть, сходится к 0 как .
Мы уже упоминали, что если непрерывно дифференцируемо, то это Коэффициент Фурье производной . следует, по существу Из неравенства Коши–Шварца , что абсолютно суммируема. Сумма этого ряда является непрерывной функцией, равной , поскольку ряд Фурье сходится в среднем к :
Теорема — Если , затем сходится к равномерно (а значит, и поточечно ).
Этот результат легко доказать, если далее предполагается, что , поскольку в этом случае стремится к нулю, так как . В более общем смысле, ряд Фурье абсолютно суммируем, поэтому сходится равномерно к , при условии, что удовлетворяет Гёльдера условию порядка . В абсолютно суммируемом случае неравенство:
доказывает равномерную сходимость.
многие другие результаты, касающиеся сходимости рядов Фурье , начиная от довольно простого результата о том, что ряд сходится при Известны если дифференцируема в , к гораздо более сложному результату Леннарта Карлесона , чем ряд Фурье функция фактически сходится почти везде .
Дивергенция [ править ]
Поскольку ряды Фурье обладают такими хорошими свойствами сходимости, многие часто удивляются некоторым отрицательным результатам. Например, ряд Фурье непрерывной T -периодической функции не обязательно сходится поточечно. [ нужна ссылка ] Принцип равномерной ограниченности дает простое неконструктивное доказательство этого факта.
В 1922 году Андрей Колмогоров опубликовал статью под названием «Серия Фурье-Лебега, расходящаяся presque partout» , в которой привел пример интегрируемой по Лебегу функции, ряд Фурье которой расходится почти всюду. Позже он построил пример интегрируемой функции, ряд Фурье которой расходится всюду. [25]
См. также [ править ]
- Теорема ATS
- Теорема Карлесона
- Ядро Дирихле
- Дискретное преобразование Фурье
- Быстрое преобразование Фурье
- Теорема Фейера
- Фурье-анализ
- Ряд Фурье по синусу и косинусу
- Преобразование Фурье
- Феномен Гиббса
- Ряд Фурье половинного диапазона
- Ряд Лорана – замена q = e IX преобразует ряд Фурье в ряд Лорана и наоборот. Это используется в q в ряд разложении j -инварианта .
- Спектральный анализ методом наименьших квадратов
- Многомерное преобразование
- Спектральная теория
- Теория Штурма – Лиувилля
- по теореме о вычетах Интегралы от f ( z ), особенности, полюса
Примечания [ править ]
- ^ Но , в общем.
- ^ Поскольку интеграл, определяющий преобразование Фурье периодической функции, не сходится, необходимо рассматривать периодическую функцию и ее преобразование как распределения . В этом смысле — это дельта-функция Дирака , которая является примером распределения.
- ↑ проделали важную раннюю работу над волновым уравнением Эти трое , особенно Даламбер, . Работы Эйлера в этой области были в основном одновременны/в сотрудничестве с Бернулли , хотя последний внес некоторый самостоятельный вклад в теорию волн и вибраций. (См. Феттер и Валецка, 2003 , стр. 209–210).
- ^ Эти слова не принадлежат строго Фурье. Хотя в цитируемой статье автором указан Фурье, в сноске указано, что статья на самом деле была написана Пуассоном (что она не была написана Фурье, это также ясно из постоянного использования третьего лица для ссылки на него) и что это , «по причинам исторического интереса», представлено так, как если бы это были оригинальные мемуары Фурье.
Ссылки [ править ]
- ^ «Фурье» . Dictionary.com Полный (онлайн). nd
- ^ Зигмунд, А. (2002). Тригонометрическая серия (3-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 0-521-89053-5 .
- ^ Пинкус, Аллан; Зафрани, Сами (1997). Ряд Фурье и интегральные преобразования (1-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. стр. 42–44. ISBN 0-521-59771-4 .
- ^ Толстов, Георгий П. (1976). Ряд Фурье . Курьер-Дувр. ISBN 0-486-63317-9 .
- ^ Стиллвелл, Джон (2013). «Логика и философия математики в девятнадцатом веке» . В Тен, CL (ред.). Рутледж История философии . Том. VII: Девятнадцатый век. Рутледж. п. 204. ИСБН 978-1-134-92880-4 .
- ^ Фассауэр, Грег (2015). «Ряд Фурье и краевые задачи» (PDF) . Конспекты курса Math 461, глава 3 . Кафедра прикладной математики Иллинойского технологического института . Проверено 6 ноября 2020 г.
- ^ Каджори, Флориан (1893). История математики . Макмиллан. п. 283 .
- ^ Лежен-Дирихле, Питер Густав (1829). «О сходимости тригонометрических рядов, служащих для представления произвольной функции между двумя заданными пределами» . Journal für die reine und angewandte Mathematik (на французском языке). 4 : 157–169. arXiv : 0806.1294 .
- ^ «О представимости функции тригонометрическим рядом» . Кандидатская диссертация , Геттинген ; 1854. Трактаты Королевского общества наук в Геттингене , вып. 13, 1867. Опубликовано посмертно для Римана Рихардом Дедекиндом (на немецком языке). Архивировано из оригинала 20 мая 2008 года . Проверено 19 мая 2008 г.
- ^ Маскр, Д.; Риман, Бернхард (1867), «Посмертная диссертация о представлении функций тригонометрическими рядами», в Граттан-Гиннессе, Айвор (редактор), « Важные сочинения по западной математике 1640–1940» , Elsevier (опубликовано в 2005 г.), стр. 49, ISBN 9780080457444
- ^ Реммерт, Рейнхольд (1991). Теория комплексных функций: Чтения по математике . Спрингер. п. 29. ISBN 9780387971957 .
- ^ Нерлав, Марк; Гретер, Дэвид М.; Карвальо, Хосе Л. (1995). Анализ экономических временных рядов. Экономическая теория, эконометрика и математическая экономика . Эльзевир. ISBN 0-12-515751-7 .
- ^ Вильгельм Флюгге , Напряжения в оболочках (1973), 2-е издание. ISBN 978-3-642-88291-3 . Первоначально опубликовано на немецком языке под названием «Статика и динамика оболочек» (1937).
- ^ Фурье, Жан-Батист-Жозеф (1888). Гастон Дарбу (ред.). Oeuvres de Fourier [ Работы Фурье ] (на французском языке). Париж: Готье-Виллар и Филс. стр. 218–219 – через Галлику.
- ^ Сепези, Г. (13 февраля 2022 г.). «Непреходящий пример Зенона» . На пути к науке о данных. стр. Приложение Б.
- ^ Jump up to: Перейти обратно: а б с д и Папула, Лотар (2009). Сборник математических формул: для инженеров и ученых [ Математические функции для инженеров и физиков ] (на немецком языке). Vieweg+Teubner Verlag. ISBN 978-3834807571 .
- ^ Jump up to: Перейти обратно: а б с д Шмалий, Ю.С. (2007). Сигналы непрерывного времени . Спрингер. ISBN 978-1402062711 .
- ^ Проакис, Джон Г.; Манолакис, Димитрис Г. (1996). Цифровая обработка сигналов: принципы, алгоритмы и приложения (3-е изд.). Прентис Холл. п. 291 . ISBN 978-0-13-373762-2 .
- ^ «Характеризации линейного подпространства, связанного с рядом Фурье» . MathOverflow. 19 ноября 2010 г. Проверено 8 августа 2014 г.
- ^ Исчезновение половины коэффициентов Фурье в шахматных массивах
- ^ Зиберт, Уильям МакК. (1985). Цепи, сигналы и системы . МТИ Пресс. п. 402. ИСБН 978-0-262-19229-3 .
- ^ Мартон, Л.; Мартон, Клэр (1990). Достижения электроники и электронной физики . Академическая пресса. п. 369. ИСБН 978-0-12-014650-5 .
- ^ Кузмани, Ганс (1998). Спектроскопия твердого тела . Спрингер. п. 14. ISBN 978-3-540-63913-8 .
- ^ Прибрам, Карл Х.; Ясуэ, Кунио; Джибу, Мэри (1991). Мозг и восприятие . Лоуренс Эрлбаум Ассошиэйтс. п. 26. ISBN 978-0-89859-995-4 .
- ^ Кацнельсон, Ицхак (1976). Введение в гармонический анализ (2-е исправленное изд.). Нью-Йорк, штат Нью-Йорк: ISBN Dover Publications, Inc. 0-486-63331-4 .
Дальнейшее чтение [ править ]
- Уильям Э. Бойс; Ричард К. ДиПрима (2005). Элементарные дифференциальные уравнения и краевые задачи (8-е изд.). John Wiley & Sons, Inc. Нью-Джерси: ISBN 0-471-43338-1 .
- Джозеф Фурье, перевод Александра Фримена (2003). Аналитическая теория тепла . Дуврские публикации. ISBN 0-486-49531-0 . Полное переиздание 2003 года английского перевода Александра Фримена 1878 года работы Фурье Théorie Analytique de la Chaleur , первоначально опубликованного в 1822 году.
- Энрике А. Гонсалес-Веласко (1992). «Связи в математическом анализе: случай рядов Фурье». Американский математический ежемесячник . 99 (5): 427–441. дои : 10.2307/2325087 . JSTOR 2325087 .
- Феттер, Александр Л.; Валецка, Джон Дирк (2003). Теоретическая механика частиц и сплошных сред . Курьер. ISBN 978-0-486-43261-8 .
- Феликс Кляйн , Развитие математики в XIX веке . Mathsci Press Brookline, Mass, 1979. Перевод М. Акермана из «Лекций по развитию математики в XIX веке» , Springer, Берлин, 1928.
- Вальтер Рудин (1976). Принципы математического анализа (3-е изд.). Нью-Йорк: McGraw-Hill, Inc. ISBN 0-07-054235-Х .
- А. Зигмунд (2002). Тригонометрический ряд (третье изд.). Кембридж: Издательство Кембриджского университета. ISBN 0-521-89053-5 . Первое издание вышло в 1935 году.
Внешние ссылки [ править ]
- «Ряды Фурье» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Хобсон, Эрнест (1911). . Британская энциклопедия . Том. 10 (11-е изд.). стр. 753–758.
- Вайсштейн, Эрик В. «Ряд Фурье» . Математический мир .
- Жозеф Фурье - сайт о жизни Фурье, который использовался для исторического раздела этой статьи в Wayback Machine (архивировано 5 декабря 2001 г.).
В эту статью включен материал из примера серии Фурье на PlanetMath , которая распространяется под лицензией Creative Commons Attribution/Share-Alike License .































![{\displaystyle [-P/2,P/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773e3d42ef176524eeb449749ec2bc0a83b5566a)
![{\displaystyle [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)







![{\displaystyle {\begin{aligned}\cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)&{}\equiv {\tfrac {1} 2}}e^{i\left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}+{\tfrac {1}{2}}e^{- i\left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}\\[6pt]&=\left({\tfrac {1}{2}}e ^{-i\varphi _{n}}\right)\cdot e^{i2\pi {\tfrac {+n}{P}}x}+\left({\tfrac {1}{2}}e ^{-i\varphi _{n}}\right)^{*}\cdot e^{i2\pi {\tfrac {-n}{P}}x}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b4e16273af487d058c192627d139fe8fca55e67)








![{\displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
![{\displaystyle \mathrm {X} _{f}(\tau)={\tfrac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\ cdot \cos \left(2\pi f(x-\tau )\right)\,dx;\quad \tau \in \left[0,{\tfrac {1}{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ae1bbd189d0cd0cdc4218a2b78ced49bcc11d89)







![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi)&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left (2\pi {\tfrac {n}{P}}x-\varphi \right)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)\,dx } _{A}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)\,dx} _{B}\\&=\cos(\varphi )\cdot A+\sin(\varphi )\cdot B\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24287ecc41a76aacf2f640f52674dbcfcee07d21)






![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s(x)&=\sum _{n=-\infty }^{\infty }{\widehat {s}}(n)\cdot e^{i2\pi {\ tfrac {n}{P}}x}&&\scriptstyle {\text{общематематическое обозначение}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{ i2\pi {\tfrac {n}{P}}x}&&\scriptstyle {\text{общее инженерное обозначение}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab1656144664ad56f8ed36ac280fbf9401ea7da9)
![{\displaystyle S(f)\ \triangleq \ \sum _ {n=-\infty }^{\infty }S[n]\cdot \delta \left(f- {\frac {n}{P}}\ верно),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _ {n=-\infty }^{\infty }S[n]\cdot \delta \left(f- {\frac {n}{P}}\right)\right)e^{i2\pi fx}\ ,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f -{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[ n]\cdot e^{i2\pi {\tfrac {n}{P}}x}\ \ \triangleq \ s_ {\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10002996a7c3e5b28df028d7096c4c00efee99c6)

![{\displaystyle (-\пи,\пи]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)


![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\, dx=0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x) \sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n ^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60820ad01df637675beb2c56a9db388cd0539490)

![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[A_{n}\ cos \left(nx\right)+B_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1 }^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \ (x-\pi )\ {\text{ не кратно }}\ 2\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b5b85f18c97953fdf678240a1f7d70bc15abbdb)

![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)












![{\displaystyle (x,y)\in [0,\pi]\times [0,\pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)























![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle а\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i2\pi {\tfrac {x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c56731e1382c8189ca81104cbade4d310fd72d8)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\textstyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }^{\infty }{\ Бигл |}S[n]{\Bigr |}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90e7f4dd99392022f87674ed1c8ea8306634bc28)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)



![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=in{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle {\widehat {s^{(k)}}}[n]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)


![{\displaystyle [-\пи,\пи]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\пи,\пи]\times [-\пи,\пи]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\ \[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^ {\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}} \int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\tfrac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0} ^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{ 2},x_{3})\cdot e^{-i2\pi \left({\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}} {a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/257f40440f195f996a7a7df57b110f544e8553c6)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}} \int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\tfrac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0} ^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{ 1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left( {\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}}{a_{2}}}x_{2}+{\tfrac {m_{3} }{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e16c337b17dc4ed299de47b108a2ff7eb060b9f3)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}} & {\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\ частичное x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y }}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_ {3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi,\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)












![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i2\pi {\tfrac {n}{P}}x} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5a3caa42e24c74a3efb0abdf3eb44ad068f7eb5)

![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i2\pi {\tfrac {n}{P}}x} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef1c25f3121bf8a28e6ae0a7d00eef1b2953f1dc)







![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)


![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)



